Leetcode 96. Different binary search trees

96. Different binary search trees

Give you an integer n , Seek just by n Composed of nodes with node values from 1 To n Different from each other Binary search tree How many kinds? ？ Returns the number of binary search trees satisfying the meaning of the question .
Example 1：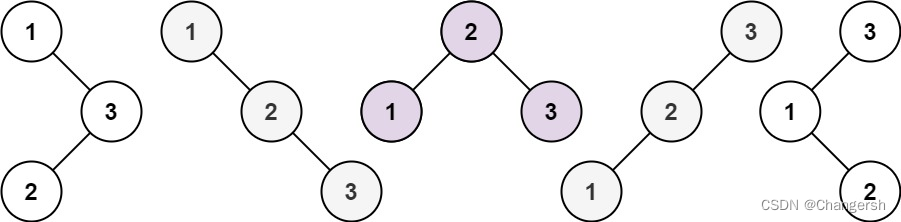

Input ：n = 3
Output ：5

Example 2：

Input ：n = 1
Output ：1

Tips ：

1 <= n <= 19

Ideas

We can n = 1 2 3 All three cases are listed , Then we can find out ：
n = 1 when , There is only one node , The value is 1, It can only form a binary search tree .
n = 2 when ,1 2 Sure 1 For the node , It's fine too 2 Root node , So there are two cases .
n = 3 when , This is the case in the above figure , There are five situations , It can be divided into three categories ：

1. 1 Root node ： The rest are better than 1 Big , So the left subtree has 1 - 1 = 0 Nodes , Right subtree has 3 - 1 = 2 Nodes , Then the situation becomes two nodes of the right subtree , The left subtree has zero nodes . So the number of times = The left subtree 0 Number of types of nodes * Right subtree 2 Number of types of nodes
2. 2 Root node ： The left subtree 2 - 1 = 1 Nodes , Right subtree 3 - 2 = 1 Nodes , So the number of times = A node of the left subtree * A node of the right subtree
3. 3 Root node ： The left subtree 3 - 1 = 2 Nodes , Right subtree 3 - 3 = 0 Nodes , So the number of times = Two nodes of left subtree * A node of the right subtree

And we can also know , Whether the left subtree or the right subtree, the number of types of corresponding nodes is equal to dp[i] Value .
therefore dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2];
For the first i Nodes , Consider starting from 1 To i As the root node , So you need to add up
Is the total i Nodes , For the root node j , here , Zuo Zi Shu you j - 1 Nodes , Right subtree has i - j Nodes

Code

class Solution {
    
public:
    int numTrees(int n) {
    
        int dp[n + 1];
        for (int i = 0; i <= n; i++) dp[i] = 0;
        dp[0] = 1;

        for (int i = 1; i <= n; i++) {
    
            for (int j = 1; j <= i; j++) {
    
                dp[i] += dp[i - j] * dp[j - 1];
            }
        }

        return dp[n];
    }
};
/* // For the first i Nodes , You need to consider 1 As the root node until i As the root node , So you need to add up  // altogether i Nodes , For the root node j when , The number of nodes in the left subtree is j-1, The number of nodes in the right subtree is i-j */

/*  Elements 1 The number of search trees for the head node  =  Right subtree has 2 Number of search trees of elements  *  Zuo Zi Shu you 0 Number of search trees of elements   Elements 2 The number of search trees for the head node  =  Right subtree has 1 Number of search trees of elements  *  Zuo Zi Shu you 1 Number of search trees of elements   Elements 3 The number of search trees for the head node  =  Right subtree has 0 Number of search trees of elements  *  Zuo Zi Shu you 2 Number of search trees of elements   Yes 2 The number of search trees per element is dp[2].  Yes 1 The number of search trees per element is dp[1].  Yes 0 The number of search trees per element is dp[0].  therefore dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2] */