4. Talk about the famous Zhang Zhengyou calibration method

---

0、 Zhang Zhengyou calibration method paper

This blog article refers to two papers of Dr. zhangzhengyou ：Flexible camera calibration by viewing a plane from unknown orientation and A Flexible New Technique for Camera Calibration

1、 Zhang Zhengyou calibration method

First , We learned Camera imaging model , Through that model , It is easy to understand the following formula .

hinder $r_i$ and $t$ Is the column vector representation of the external parameter matrix , The advantage of this writing is that some constraints can be constructed by using the properties of the rotation matrix .

1.0 The properties of rotation matrix

① Modules of each row and column , All for 1;
② Any two column vectors or any two row vectors are orthogonal ;
③ The inverse of an orthogonal matrix is equal to the transpose of an orthogonal matrix .

Later, we will use the properties of the above rotation matrix .

1.1 Solve homography matrix

We use a plane calibration plate for calibration （ Take checkerboard as an example ）, We will $XOY$ The plane is set on the plane of the calibration plate , The axis is vertically outward , In this way, all feature points detected have
$Z_w=0$ The relationship between .

Bring in the above formula , There will be ：

because $Z_w=0$, So we eliminated $r_3$.
Make $A[r_1,r_2,r_3]=H$, Then there are ,
$s[u,v,1{]}^T=H[X_w,Y_w,1{]}^T$
This $H$ Is homography matrix , We expand it to ,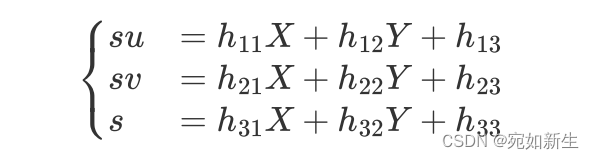

In this way, we know the number of points on the chessboard 3D coordinate （ We know the size of the chessboard ）, And the pixel coordinates of each corresponding corner on the image plane , You can put the $h_{ij}$ It's solved .

And then $s$ The first two equations are ,

in other words ,$H$ Yes 8 A degree of freedom . About the degree of freedom of several matrices, we can see My blog .
Definition $h^{\prime }=[h_{11},h_{12},h_{13},h_{21},h_{22},h_{23},h_{31},h_{32},1]$,

above $X,Y,u,v$ All known quantities . Because homography matrix has 8 A degree of freedom , A pair of matching points can build the above 2 A constraint , therefore 4 The homography matrix can be solved by matching points , Due to noise , In reality, nonlinear optimization method is often used to solve , Like singular value decomposition +LM etc. .
We write the above formula as $S{h}^{\prime }=0$ , coefficient matrix $S^{T}S$ The eigenvector corresponding to the minimum eigenvalue is the overdetermined equations $S{h}^{\prime }=0$ The least square solution of .

1.2 Solve the internal parameter matrix

The homography matrix we obtained above may have a scaling factor with the real value , We add a scale factor , Yes

from 1.0 Two constraints can be obtained from the properties of the rotation matrix mentioned in section :

So there is ,


It can be seen from the red letter derivation above , The formula in the picture is actually like this $\lambda ={\lambda }^2$, We think it is a constant scaling factor . Just write him down as $\lambda$ that will do .
because $A$ Is an internal parameter matrix , We can calculate his inverse matrix .
$$A=\left[\begin{array}{ccc}\alpha & \gamma & u_0\\ 0& \beta & v_0\\ 0& 0& 1\end{array}\right]$$

among ,$\alpha ,\beta$ Indicates the focal length in both directions ,$u_0,v_0$ Represents the primary point . Early cameras may have the problem that the pixels themselves are parallelograms rather than rectangles , So add a parameter $\gamma$ To describe , This parameter can also be considered as an approximation of the deformation caused by the lax placement of the sensor perpendicular to the main optical axis of the camera , Facts and pixel coordinates X,Y The tangent of the included angle between the axes is inversely proportional , So when $\gamma$=0 when , Pixels are rectangular .
Make $B=A^{-T}{A}^{-1}$, Then there are ：


because $h_1$ There are three elements , So there is this expression .
As for why we put $B$ When the matrix is spread into a vector , Leaving only 6 Elements , Actually, calculate this $B$ You know the .

thus , The previous constraint equation is simplified to ：

among ,$v$ Are known quantities , This constitutes another $Sh=0$ The equation of . We know , Each calibration chart can provide one of the above constraints ( Corresponding to one $H$), And each equation will provide two constraint equations . $B$ It has 6 Location elements , So theoretically , Three calibration pictures can solve the above equation . When the calibration chart exceeds 3 Zhang Shi , The least square method can also be used to solve the corresponding overdetermined equation . Singular value decomposition and LM Method to get $B$.
obtain $B$ after , It can be based on $B$ The relationship with the elements of the internal parameter matrix is solved $\alpha ,\beta ,\gamma ,u_0,v_0$ Come on .

1.3 Solve the external parameter matrix

We know （ Including the scale factor ）
$[h_1,h_2,h_3]=A[r_1,r_2,t]$
Here we have solved $HandA$, And according to the front 1.0 Properties of nodal rotation matrix , So there is ,

At this time, there is a difference $r_3$, It's simple ,
$r_3=r_{1}X{r}_2$（ Cross riding ）.
Only this and nothing more , Internal and external parameters are calculated .
Because there is noise in the image , So what we got $R$ In fact, it does not necessarily satisfy the property of orthogonality , Therefore, use the optimization method to get the best $R$ ,
It is said in the author's original text ：


If you are interested, you can explore by yourself .

1.4 Solve distortion coefficient

In the paper ：

1.5 Nonlinear optimization

Be careful ： The above series of operations are to get the initial value of each parameter , With the initial value , We can use the camera model + Distortion model on the chessboard 3d Point projection , Establish the re projection error equation , Then the accurate values of each parameter are obtained by using the nonlinear optimization method .
Nonlinear optimization methods can be referred to This article I collated .

2、 What is the use of homography matrix

On homography matrix , I recommend reading Liuge's official account article Magic homography matrix .

---

3、 Thank you very much for reading ！