当前位置:网站首页>12.< tag-动态规划和子序列, 子数组>lt.72. 编辑距离
12.< tag-动态规划和子序列, 子数组>lt.72. 编辑距离
2022-07-29 01:15:00 【菜菜的大数据开发之路】
lt.72. 编辑距离
[案例需求]

[思路分析. 动态规划]
- 确定dp数组以及下标的含义
dp[i][j] 表示:
以下标i - 1为结尾的字符串word1(也就是长度为i的字符串word1), 和以下标j - 1为结尾的字符串word2, 最近编辑距离为dp[i][j];
这里在强调一下:为啥要表示下标i-1为结尾的字符串呢,为啥不表示下标i为结尾的字符串呢?
用i来表示也可以! 但我统一以下标i-1为结尾的字符串,在下面的递归公式中会容易理解一点。
- 确定递推公式
确定递推公式时, 首先要考虑清楚编辑的几种操作:
if(word1[i - 1] == word2[i- 1]) 不操作
if(word[i- 1] != word2[i - 1]){
增/删/改
}

那么,
if (word1[i - 1] != word2[j - 1]),此时就需要编辑了,如何编辑呢?
- 操作一: word1删除一个元素, 那么就是以下标i - 2为结尾的word1与j - 1为结尾的word2的最近编辑距离再加上一个操作., 即
dp[i][j] = dp[ i - 1][j] + 1;- 操作二, word2删除一个元素, 那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作, 即
dp[i][j] = dp[i][j - 1] + 1;- 操作三. 替换元素, 操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增加元素,那么以下标i-2为结尾的word1 与 j-2为结尾的word2的最近编辑距离 加上一个替换元素的操作。
即 dp[i][j] = dp[i - 1][j - 1] + 1;
- 所以, 递推公式如下:
if (word1[i - 1] == word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
}
else {
dp[i][j] = min({
dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}
- dp数组的初始化
我们在回顾一下dp[i][j]的定义;
dp[i][j] 表示长度为j, 即以下标i- 1结尾的字符串word1, 和以下标为j - 1为结尾的字符串word2, 最近编辑距离为dp[i][j]
又因为, 我们由递推公式得知, 需要初始化 dp[0][0], dp[i][0], dp[0][j]三种元素.
那么他们代表什么呢?
dp[i][0] :以下标i-1为结尾的字符串word1,和空字符串word2,最近编辑距离为dp[i][0], 显然为i, 即删除i次
那么dp[i][0]就应该是i,对word1里的元素全部做删除操作,即:dp[i][0] = i;
同理, 同理dp[0][j] = j;
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
- 确定遍历顺序
- 举例推导dp数组
[代码实现]
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
//1. dp数组, dp[i][j]表示长度为i的字符串word1和长度为j的字符串word2, word1转换为word2需要的编辑距离
int[][] dp = new int[len1 + 1][len2 + 1];
//2. 确定递推公式;
//word1[i] 和word[j] 在某个索引处, 存在着字符相等或不相等两种情况
//字符相等的话, 我们在此处索引的编辑距离为0,
//字符不相等的话, 我们又有三种操作方式
//1. 删除一个字符, 如果删除word1[i - 1]能够使得word1[i - 2] == word2[j - 1],
那么, dp[i][j] = dp[i - 1][j] + 1;
如果删除word2[i - 1]能够使word1[i - 1] == word2[j - 2]
/那么, dp[i][j] = dp[i][j - 1] + 1;
//2. 插入一个字符, 其实跟删除是一样的效果
//3. 替换一个字符.替换word1[i] 或者word[j]
那么. dp[i][j] = dp[i - 1][j - 1] + 1;
//3. 初始化, 由递推公式可知, dp[0][0], dp[i][0], dp[0][j]需要初始化
//根据dp数组的定义, 很容易能想到初始化的值,
for(int i = 1; i <= len1; i++){
dp[i][0] = i;
}
for(int j = 1; j <= len2; j++){
dp[0][j] = j;
}
//4. 递推
for(int i = 1; i < len1 + 1; i++){
for(int j = 1; j < len2 + 1; j++){
if(word1.charAt(i - 1) == word2.charAt(j - 1)){
dp[i][j] = dp[i - 1][j - 1];
}else{
dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
}
}
}
return dp[len1][len2];
}
}
边栏推荐
- druid. io kill -9 index_ Realtime traceability task
- The basic concept of transaction and the implementation principle of MySQL transaction
- Super scientific and technological data leakage prevention system, control illegal Internet behaviors, and ensure enterprise information security
- Leetcode/ and continuous shortest subarray greater than or equal to target
- Random talk on distributed development
- [the road of Exile - Chapter 5]
- StoneDB 邀请您参与开源社区月会!
- druid. The performance of IO + tranquility real-time tasks is summarized with the help of 2020 double 11
- 【流放之路-第五章】
- TDA75610-I2C-模拟功放I2C地址的确定
猜你喜欢

JS timer setinterval clearinterval delayer setTimeout asynchronous animation

The information security and Standardization Commission issued the draft for comments on the management guide for app personal information processing activities

StoneDB 邀请您参与开源社区月会!
![[云原生]微服务架构是什么](/img/84/a0ec68646083f3539aa39ad9d98749.png)
[云原生]微服务架构是什么

Monadic linear function perceptron: Rosenblatt perceptron
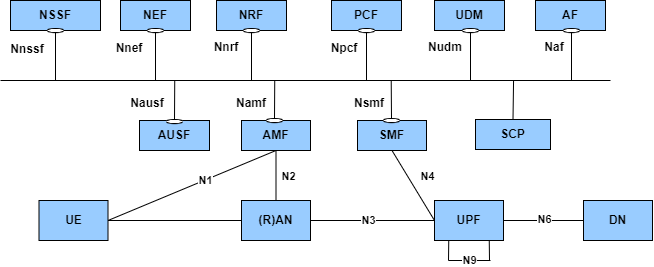
【云原生与5G】微服务加持5G核心网

知道创宇上榜CCSIP 2022全景图多个领域

How to find the right agent type? Multi angle analysis for you!

【Golang】- runtime.Goexit()

数学建模——公交调度优化
随机推荐
【流放之路-第二章】
[10:00 public class]: application exploration of Kwai gpu/fpga/asic heterogeneous platform
数学建模——仓内拣货优化问题
Event express | Apache Doris Performance Optimization Practice Series live broadcast course is open at the beginning. You are cordially invited to participate!
Lua log implementation -- print table
Solution of Lenovo notebook camera unable to open
[the road of Exile - Chapter 5]
Web crawler API Quick Start Guide
【公开课预告】:快手GPU/FPGA/ASIC异构平台的应用探索
Lm13 morphological quantification momentum period analysis
Planning mathematics final simulation exam I
Mathematical modeling -- heat conduction of subgrade on Permafrost
[7.21-26] code source - [sports festival] [Dan fishing war] [maximum weight division]
(cvpr-2019) selective kernel network
Comprehensive explanation of "search engine crawl"
E-commerce keyword research helps data collection
How companies make business decisions -- with the help of data-driven marketing
[7.21-26] code source - [square count] [dictionary order minimum] [Z-type matrix]
Google Cloud Spanner的实践经验
Random talk on distributed development


