当前位置:网站首页>【点云处理之论文狂读前沿版10】—— MVTN: Multi-View Transformation Network for 3D Shape Recognition
【点云处理之论文狂读前沿版10】—— MVTN: Multi-View Transformation Network for 3D Shape Recognition
2022-07-03 08:53:00 【LingbinBu】
MVTN: Multi-View Transformation Network for 3D Shape Recognition
摘要
- 问题: 在众多的点云处理方法中,Multi-view projection 方法的视角往往是启发式地设置或者是对所有形状都是相同的设置。
- 方法: 提出了一种方法,学习如何更好地设置这些视角。
- 细节: 引入了 Multi-View Transformation Network (MVTN),用于寻找用于3D形状识别的最优视角,整个网络的设计都是可导的。MVTN可以通过端到端的形式进行训练,并搭配任意的多视角网络用于3D形状识别。本文将MVTN和一个新的适应性多视角网络进行整合,该网络不仅可以处理3D mesh,还可以处理点云。
- 代码:https://github.com/ajhamdi/MVTN Pytorch版本

相关工作
- MVTN学习输入数据的空间变换,学习的过程中不使用额外的监督,也不调整学习过程。
方法
Overview of Multi-View 3D Recognition
多视角网络的训练可以表示为:
arg min θ C ∑ n N L ( C ( X n ) , y n ) = arg min θ C ∑ n N L ( C ( R ( S n , u 0 ) ) , y n ) \begin{aligned} & \underset{\boldsymbol{\theta}_{\mathbf{C}}}{\arg \min } \sum_{n}^{N} L\left(\mathbf{C}\left(\mathbf{X}_{n}\right), y_{n}\right) \\ =& \underset{\boldsymbol{\theta}_{\mathbf{C}}}{\arg \min } \sum_{n}^{N} L\left(\mathbf{C}\left(\mathbf{R}\left(\mathbf{S}_{n}, \mathbf{u}_{0}\right)\right), y_{n}\right) \end{aligned} =θCargminn∑NL(C(Xn),yn)θCargminn∑NL(C(R(Sn,u0)),yn)
其中 L L L 是具体任务的损失函数, N N N是数据集中3D形状的数量, y n y_{n} yn是第 n n n个3D形状 S n \mathbf{S}_{n} Sn的label。 u 0 ∈ R τ \mathbf{u}_{0} \in \mathbb{R}^{\tau} u0∈Rτ是整个数据集的 τ \tau τ个场景参数集合,这些参数表示了影响渲染图片的性质,包括视点、光线、颜色和背景。 R \mathbf{R} R是渲染器,以形状 S n \mathbf{S}_{n} Sn和参数 u 0 \mathbf{u}_{0} u0作为输入,得到每个形状的 M M M个多视角图像 X n \mathbf{X}_{n} Xn。在MVCNN中, C = MLP ( max i f ( x i ) ) \mathbf{C}=\operatorname{MLP}\left(\max _{i} \mathbf{f}\left(\mathbf{x}_{i}\right)\right) C=MLP(maxif(xi)), f : R h × w × c → R d \mathbf{f}: \mathbb{R}^{h \times w \times c} \rightarrow \mathbb{R}^{d} f:Rh×w×c→Rd是一个2D CNN backbone;在ViewGCN中, C = MLP ( c a t G C N ( f ( x i ) ) ) \mathbf{C}=\operatorname{MLP}\left(\right. cat \left._{\mathrm{GCN}}\left(\mathbf{f}\left(\mathbf{x}_{i}\right)\right)\right) C=MLP(catGCN(f(xi))), c a t G C N cat _{\mathrm{GCN}} catGCN是从图卷积网络中学习到的视图特征聚合。 θ C \boldsymbol{\theta}_{\mathbf{C}} θC是多视图网络 C \mathbf{C} C的参数。在实验部分,场景参数 u \mathbf{u} u表示成指向目标中心的相机视角的方位角(azimuth) 和仰角 (elevation) angles,因此 τ = 2 M \tau=2M τ=2M

Multi-View Transformation Network (MVTN)
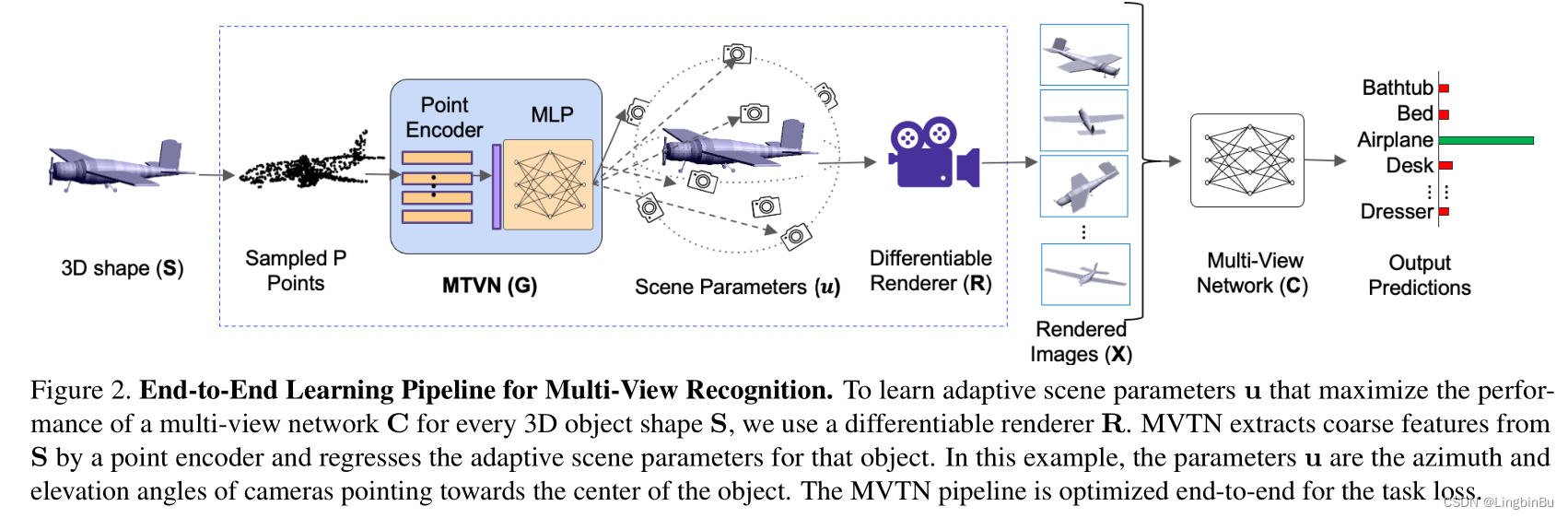
之前的多视图方法都是以图像 X \mathbf{X} X作为3D形状的唯一表示,其中 X \mathbf{X} X是使用固定的场景参数 u 0 \mathbf{u}_0 u0得到的。相反,本文考虑一个更通用的情况,将 u \mathbf{u} u设置成边界为 ± u bound \pm \mathbf{u}_{\text {bound }} ±ubound 内的变量,其中 u bound \mathbf{u}_{\text {bound }} ubound 是正数,定义了场景参数的允许范围。将每个方位角和仰角的 u bound \mathbf{u}_{\text {bound }} ubound 分别设置为 18 0 ∘ 180^{\circ} 180∘ 和 9 0 ∘ 90^{\circ} 90∘。
Differentiable Renderer
渲染器 R \mathbf{R} R以3D形状 S \mathbf{S} S(mesh or point cloud)和场景参数 u \mathbf{u} u作为输入,输出是对应的 M M M个图像 { x i } i = 1 M \left\{\mathbf{x}_{i}\right\}_{i=1}^{M} { xi}i=1M。由于 R \mathbf{R} R可导,梯度 ∂ x i ∂ u \frac{\partial \mathbf{x}_{i}}{\partial \mathbf{u}} ∂u∂xi可以从每个图像反向传播到整个场景参数,因此能够构造一个端到端的学习框架。
当 S \mathbf{S} S表示为3D mesh时, R \mathbf{R} R有两个分量:rasterizer 和 shader。首先,在给定相机视角和将face分配给像素后,rasterizer将mesh从世界坐标系变换到视图坐标系中。然后shader根据face的分配对每个像素创建多个值,并将这些值进行融合。
当 S \mathbf{S} S表示为点云时, R \mathbf{R} R可以使用alpha-blending mechanism。
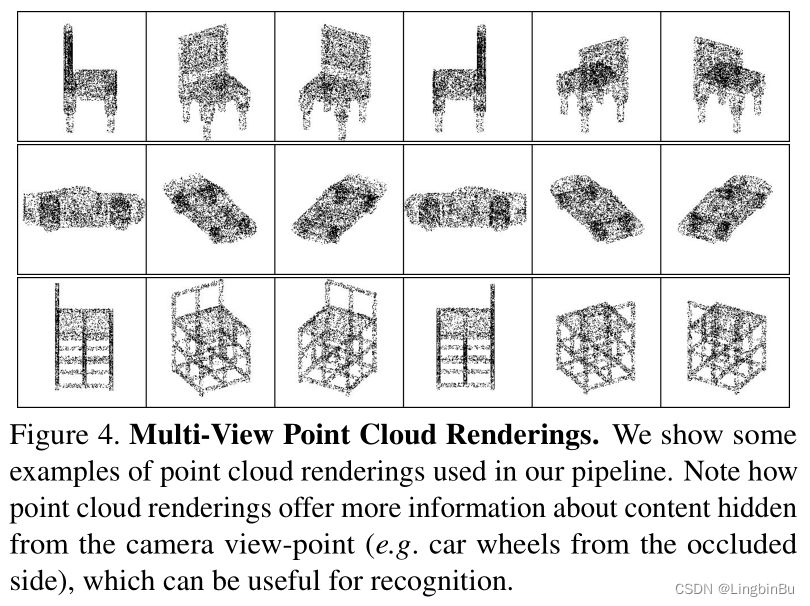
View-Points Conditioned on 3D Shape
通过学习Multi-View Transformation Network (MVTN) G ∈ R P × 3 → R τ \mathbf{G} \in \mathbb{R}^{P \times 3} \rightarrow \mathbb{R}^{\tau} G∈RP×3→Rτ和参数 θ G \boldsymbol{\theta}_{\mathbf{G}} θG,将 u \mathbf{u} u设计成3D形状的函数,其中 P P P是从形状 S \mathbf{S} S采样得到点的数量。MVTN的训练可以表示为:
arg min θ C , θ G ∑ n N L ( C ( R ( S n , u n ) ) , y n ) s. t. u n = u bound ⋅ tanh ( G ( S n ) ) \begin{aligned} \underset{\boldsymbol{\theta}_{\mathbf{C}}, \boldsymbol{\theta}_{\mathrm{G}}}{\arg \min } & \sum_{n}^{N} L\left(\mathbf{C}\left(\mathbf{R}\left(\mathbf{S}_{n}, \mathbf{u}_{n}\right)\right), y_{n}\right) \text { s. t. } \quad \mathbf{u}_{n}=\mathbf{u}_{\text {bound }} \cdot \tanh \left(\mathbf{G}\left(\mathbf{S}_{n}\right)\right) \end{aligned} θC,θGargminn∑NL(C(R(Sn,un)),yn) s. t. un=ubound ⋅tanh(G(Sn))
其中 G \mathbf{G} G对3D形状进行编码,预测具体任务多视图网络 C \mathbf{C} C的最优视点。由于 G \mathbf{G} G的目标仅仅是预测视点所以 G \mathbf{G} G的结构很简单,并且很轻量。与此同时,在 G \mathbf{G} G中还使用了简单的点编码器(比如PointNet中的shared MLP),用于处理从 S \mathbf{S} S得到的 P P P个点,并且生成维度为 b b b的coarse形状特征。然后shallow MLP从这个全局形状特征中回归出场景参数 u n \mathbf{u}_n un,为了将预测参数 u \mathbf{u} u的数值强制放入 ± u bound \pm \mathbf{u}_{\text {bound }} ±ubound 范围内,使用了tanh函数将 u \mathbf{u} u缩放到 ± u bound \pm \mathbf{u}_{\text {bound }} ±ubound 内。
MVTN for 3D Shape Classification
为了对MVTN进行训练,用于3D形状分类,我们定义了一个交叉熵损失函数,但是其他的损失函数和正则项也可以用。多视角网络( C \mathbf{C} C)和MVTN( G \mathbf{G} G)使用相同的损失函数共同训练。我们的网络结构的优点在于能够处理3D点云。当 S \mathbf{S} S是一组点云时,简单地将 R \mathbf{R} R定义为一个可导地点云渲染器。
MVTN for 3D Shape Retrieval
我们考虑 C \mathbf{C} C中分类器前面最后一层的特征表示,使用LFDA reduction将这些特征投影到其他空间,并且将处理后的特征作为signature描述一个形状。在测试阶段,形状signature被用于在测试集中检索最相似的形状。
实验
3D Shape Classification
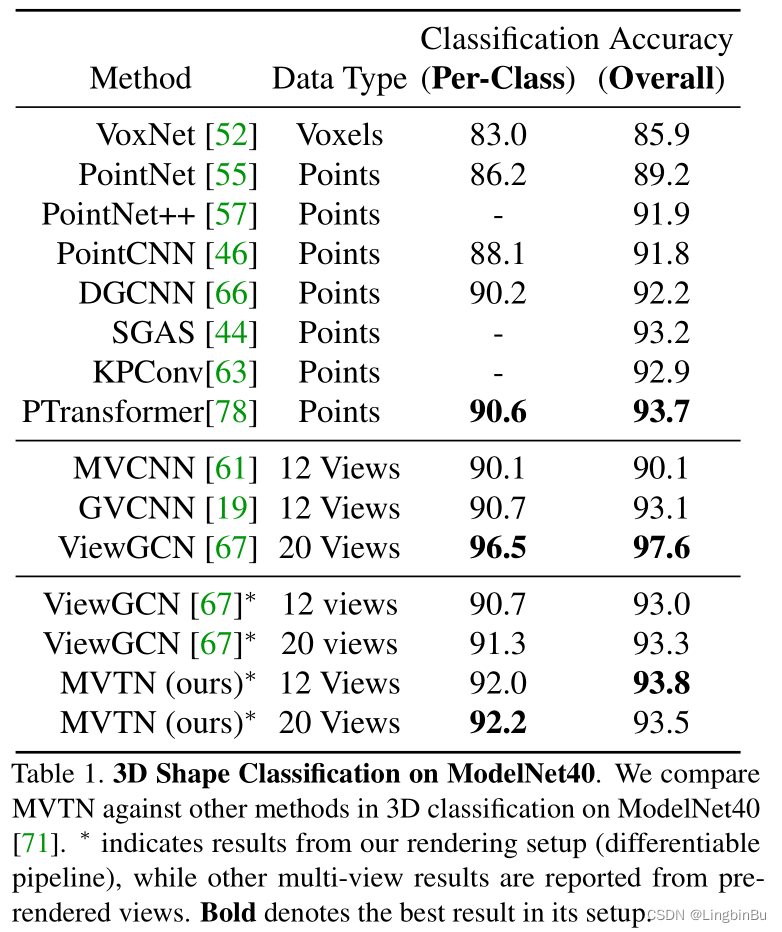
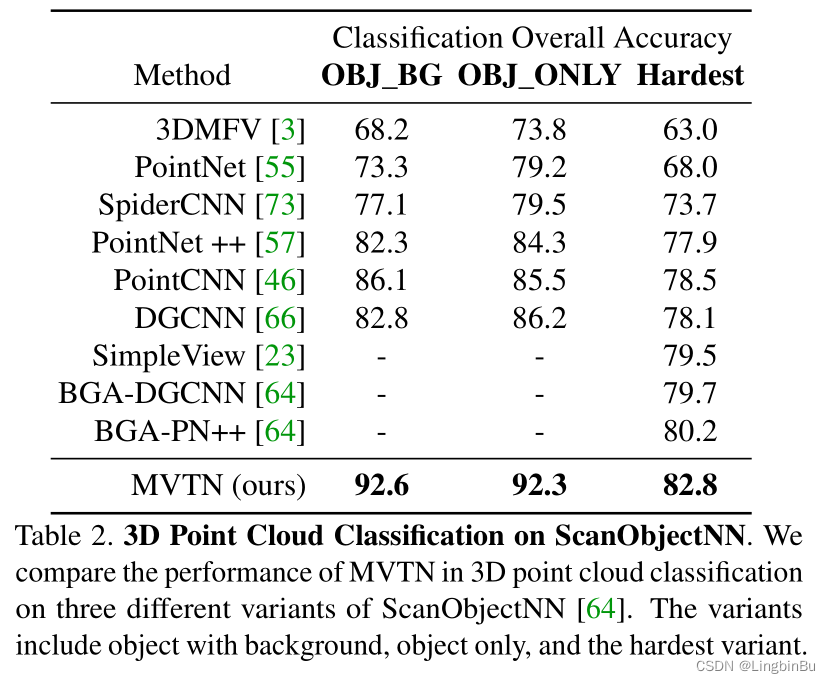
3D Shape Retrieval
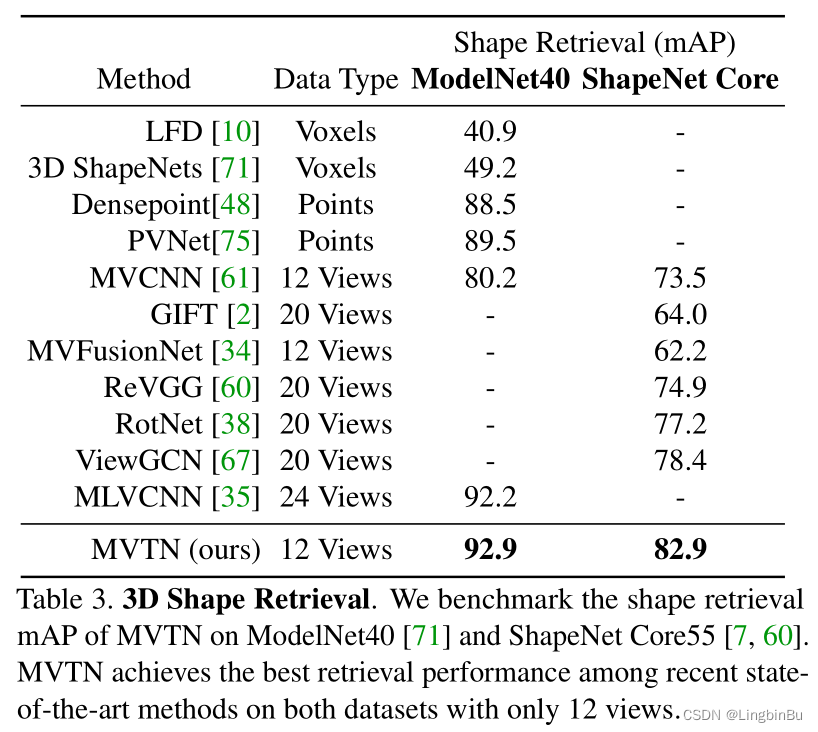

Rotation Robustness

Occlusion Robustness
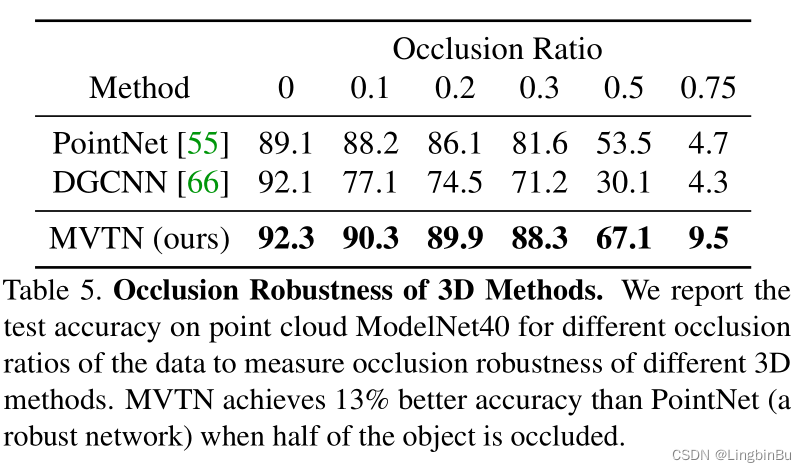

Ablation Study
Number of Views

Choice of Backbone and Point Encoders
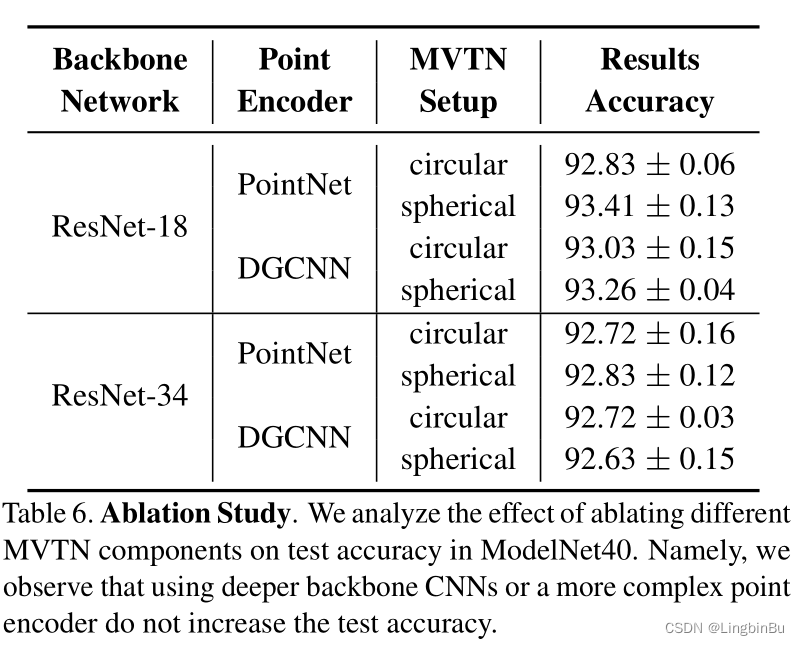
Choice of Multi-View Network

Time and Memory Requirements

边栏推荐
- TP5 order multi condition sort
- 数位统计DP AcWing 338. 计数问题
- Education informatization has stepped into 2.0. How can jnpf help teachers reduce their burden and improve efficiency?
- 22-05-26 西安 面试题(01)准备
- Too many open files solution
- 20220630 learning clock in
- Annotations simplify configuration and loading at startup
- Drawing maze EasyX library with recursive backtracking method
- Gif remove blank frame frame number adjustment
- [concurrent programming] explicit lock and AQS
猜你喜欢
Concurrent programming (V) detailed explanation of atomic and unsafe magic classes

Six dimensional space (C language)

树形DP AcWing 285. 没有上司的舞会

Binary tree sorting (C language, int type)

AcWing 785. Quick sort (template)

低代码起势,这款信息管理系统开发神器,你值得拥有!

数字化转型中,企业设备管理会出现什么问题?JNPF或将是“最优解”

How to place the parameters of the controller in the view after encountering the input textarea tag in the TP framework
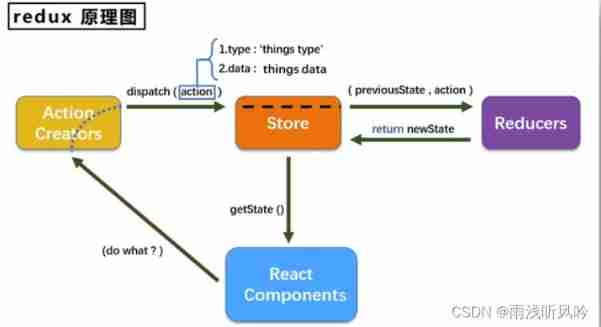
Redux - learning notes

低代码前景可期,JNPF灵活易用,用智能定义新型办公模式
随机推荐
[concurrent programming] collaboration between threads
Tree DP acwing 285 A dance without a boss
Binary tree traversal (first order traversal. Output results according to first order, middle order, and last order)
MySQL three logs
LeetCode 241. 为运算表达式设计优先级
PHP mnemonic code full text 400 words to extract the first letter of each Chinese character
AcWing 788. 逆序对的数量
使用dlv分析golang进程cpu占用高问题
Find the combination number acwing 885 Find the combination number I
20220630 learning clock in
AcWing 788. Number of pairs in reverse order
[concurrent programming] explicit lock and AQS
我们有个共同的名字,XX工
Really explain the five data structures of redis
Binary tree sorting (C language, char type)
Find the combination number acwing 886 Find the combination number II
22-05-26 Xi'an interview question (01) preparation
Drawing maze EasyX library with recursive backtracking method
Introduction to the usage of getopts in shell
Vscode connect to remote server