当前位置:网站首页>Application scenarios of Catalan number
Application scenarios of Catalan number
2022-07-03 06:39:00 【I also want to write bugs today】
List of articles
Carter LAN number
Derivation of Cartland number :
Carter LAN number (Catalan)

Application scenarios
Suppose there is n A left bracket and n Right parenthesis , How many legal combinations do they have .
Altogether C(2n,n) Combinations of , Suppose these combinations are A aggregate .
For illegal combinations , There must be a prefix , The number of right parentheses is more than that of left parentheses 1 individual , such as())(()Chinese prefix()), And the suffix must be the right bracket less than the left bracket 1 One((), We reverse the suffix ( The left bracket becomes the right bracket , The right bracket becomes the left bracket ), In this way, the right bracket in the whole combination is n+1, The left bracket is n-1. There are C(2n,n-1) Combinations of , Suppose they are B aggregate .
A Illegal combinations in can be pushed through inversion B All cases in the set , and B Collections can also be pushed out by reversing A Illegal combination in . therefore A The illegal quantity in is equal to C(2n,n-1).
Sum up , There are legal combinations C(2n,n)-C(2n,n-1) Kind of .n How many legal ways to get in and out of the stack .
The number of any prefix out of the stack must be less than the number of prefix in the stack , So this problem turns into the bracket problem above . Its combination is also C(2n,n)-C(2n,n-1) Kind of .Altogether n Nodes , How many ways to form a binary tree .
Yes 0 Nodes , The method is empty tree , The way to form a binary tree 1 Kind of .
Yes 1 Nodes , The tree is for itself ,1 Kind of .
Yes 2 Nodes , root + Left or root + Right ,2 Kind of .
Yes n Nodes , Select a node as the head node ; The left side of the head node 0 Nodes , On the right n-1 Nodes ; The left side of the head node 1 Nodes , On the right n-2 Nodes ; The left side of the head node 2 Nodes , On the right n-3 Nodes ... Can be launchedk(n)=k(0)*k(n-1)+k(1)*k(n-2)+....+k(n-2)*k(1)+k(n-1)*k(0), That is to say, the number of Cartland C(2n,n)-C(2n,n-1) Combination mode .
边栏推荐
- 剖析虚幻渲染体系(16)- 图形驱动的秘密
- ODL framework project construction trial -demo
- 有意思的鼠標指針交互探究
- Operation principle of lua on C: Foundation
- Luogu problem list: [mathematics 1] basic mathematics problems
- Cesium entity (entities) entity deletion method
- Create your own deep learning environment with CONDA
- DNS forward query:
- [system design] proximity service
- Pdf files can only print out the first page
猜你喜欢

10万奖金被瓜分,快来认识这位上榜者里的“乘风破浪的姐姐”
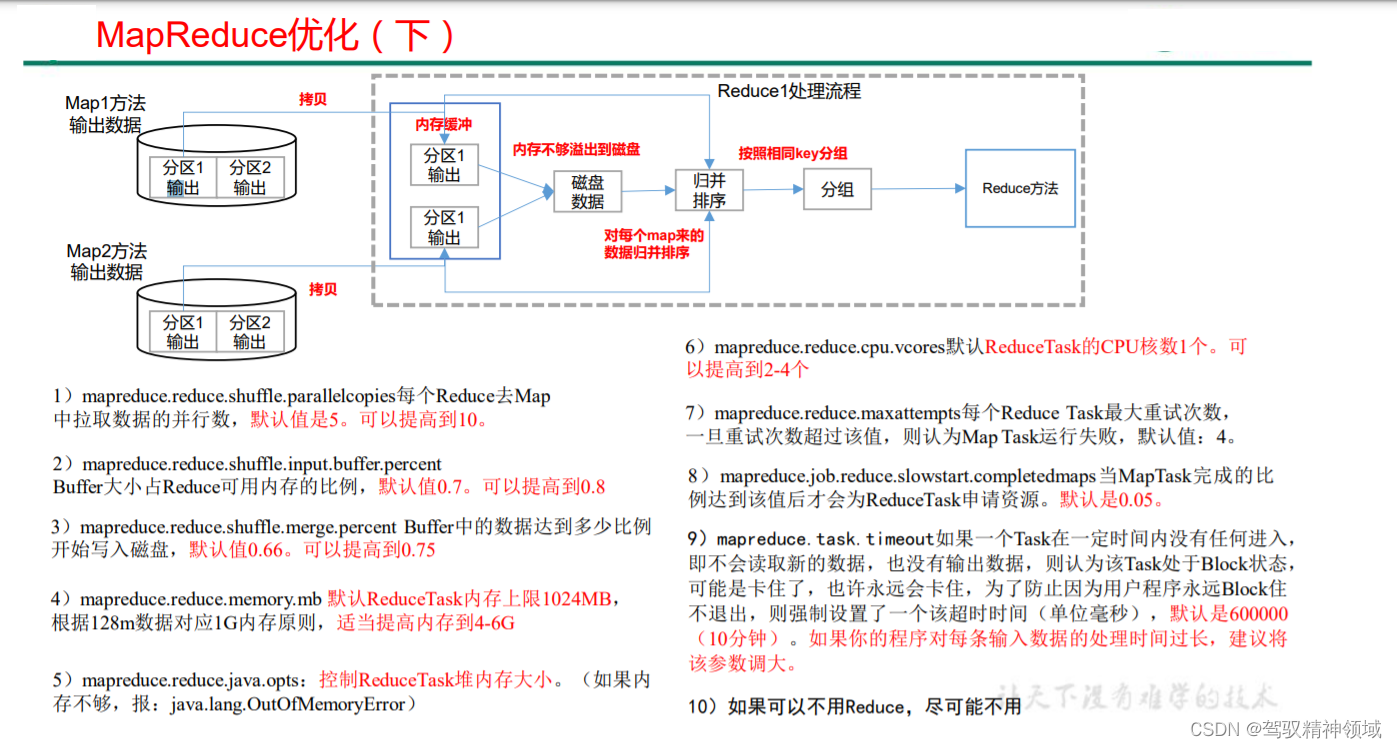
Chapter 8. MapReduce production experience

Redis cluster creation, capacity expansion and capacity reduction
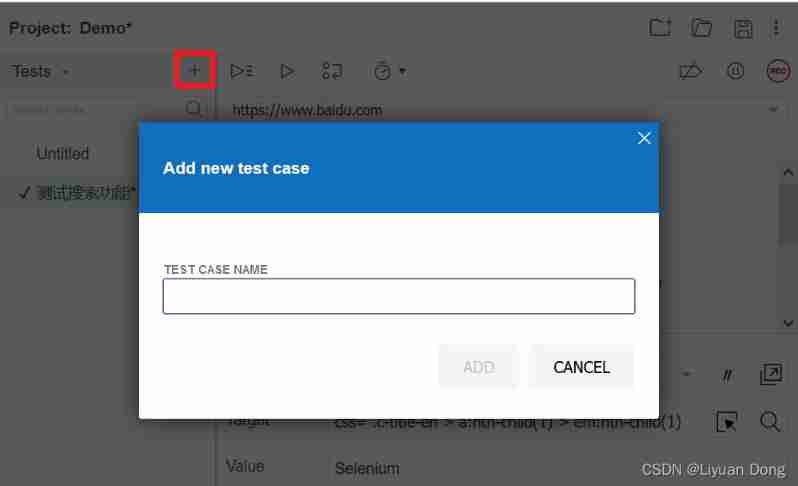
Selenium ide installation recording and local project maintenance
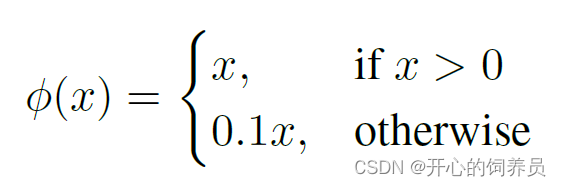
YOLOV1学习笔记
Push box games C #
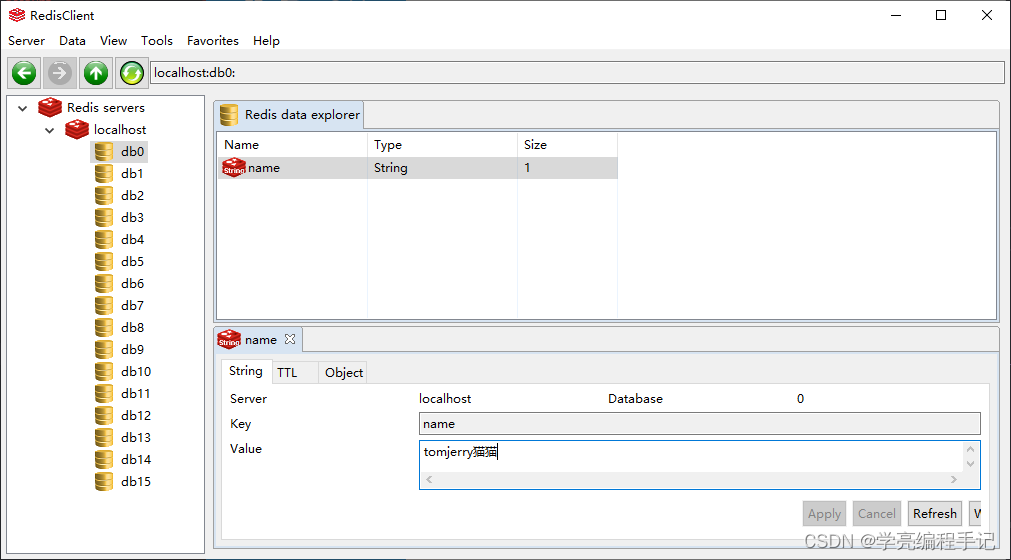
golang操作redis:写入、读取kv数据
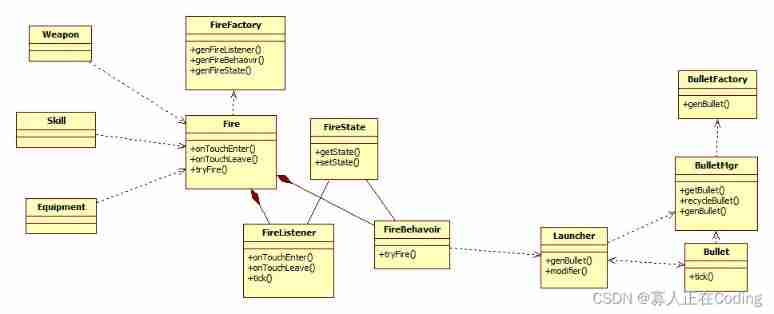
Summary of the design and implementation of the weapon system similar to the paladin of vitality
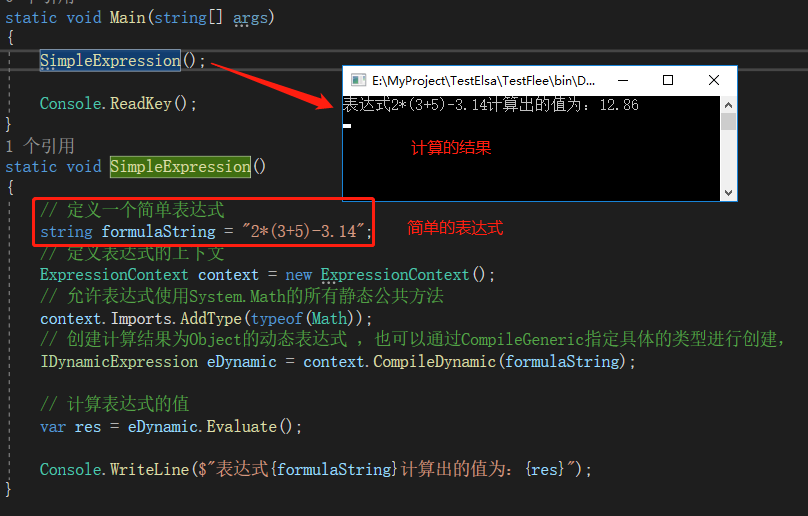
The dynamic analysis and calculation of expressions are really delicious for flee
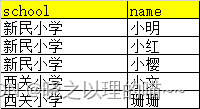
SQL implementation merges multiple rows of records into one row
随机推荐
Click cesium to obtain three-dimensional coordinates (longitude, latitude and elevation)
Condition annotation in uni-app realizes cross segment compatibility, navigation jump and parameter transfer, component creation and use, and life cycle function
SQL实现将多行记录合并成一行
Pytorch exercise items
Summary of the design and implementation of the weapon system similar to the paladin of vitality
Shell conditional statement
Printer related problem record
第8章、MapReduce 生产经验
【LeetCode】Day93-两个数组的交集 II
Important knowledge points of redis
golang操作redis:写入、读取hash类型数据
[C /vb.net] convert PDF to svg/image, svg/image to PDF
致即将毕业大学生的一封信
The difference between CONDA and pip
Scroll view specifies the starting position of the scrolling element
Advanced technology management - do you know the whole picture of growth?
Push box games C #
JMeter linked database
2022 cisp-pte (III) command execution
Code management tools