当前位置:网站首页>【GCN-RS】Are Graph Augmentations Necessary? Simple Graph Contrastive Learning for RS (SIGIR‘22)
【GCN-RS】Are Graph Augmentations Necessary? Simple Graph Contrastive Learning for RS (SIGIR‘22)
2022-07-25 11:11:00 【chad_lee】
Are Graph Augmentations Necessary? Simple Graph Contrastive Learning for Recommendation (SIGIR’22)

这篇文章抨击图对比学习不一定要扩展图结构,SGL那种方法复杂且收益微弱:

文章在SGL的基础上,测试不扩增图结构,直接对比学习:
L c l = ∑ i ∈ B − log exp ( z i ′ ⊤ z i ′ ′ / τ ) ∑ j ∈ B exp ( z i ′ ⊤ z j ′ ′ / τ ) \mathcal{L}_{c l}=\sum_{i \in \mathcal{B}}-\log \frac{\exp \left(\mathbf{z}_{i}^{\prime \top} \mathbf{z}_{i}^{\prime \prime} / \tau\right)}{\sum_{j \in \mathcal{B}} \exp \left(\mathbf{z}_{i}^{\prime \top} \mathbf{z}_{j}^{\prime \prime} / \tau\right)} Lcl=i∈B∑−log∑j∈Bexp(zi′⊤zj′′/τ)exp(zi′⊤zi′′/τ)
我曾经也做过实验,把这个公式的分子置为1,即不考虑扩增图结构后表征依然相似,NDCG指标反而升的更高,所以SGL的确实不太有用。
文章提出了一种非常简单的方法,直接在embedding上做扰动,不动图结构:
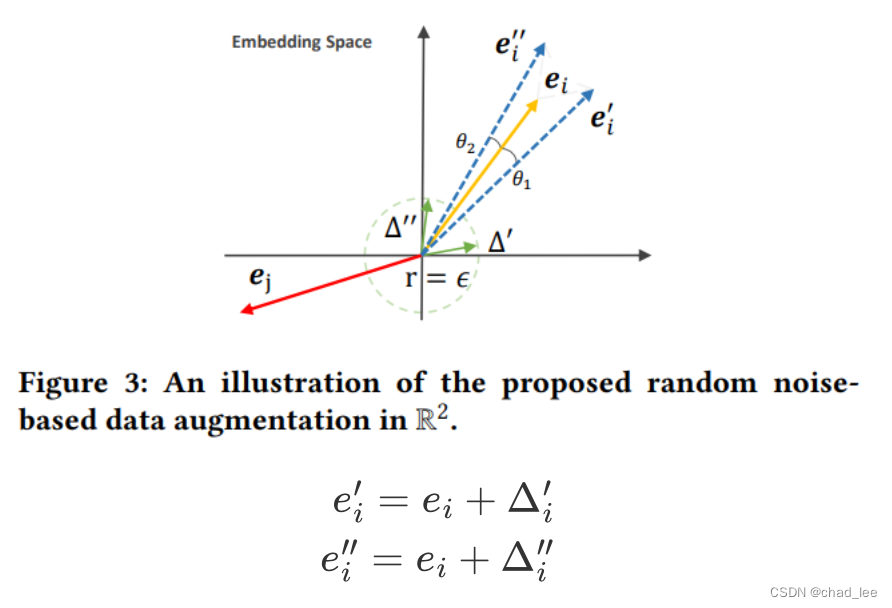
e i ′ = e i + Δ i ′ e i ′ ′ = e i + Δ i ′ ′ \begin{array}{r} e_{i}^{\prime}=e_{i}+\Delta_{i}^{\prime} \\ e_{i}^{\prime \prime}=e_{i}+\Delta_{i}^{\prime \prime} \end{array} ei′=ei+Δi′ei′′=ei+Δi′′
其中 Δ i ′ , Δ i ′ ′ \Delta_{i}^{\prime },\Delta_{i}^{\prime \prime} Δi′,Δi′′分别是随机扰动, Δ = Δ ˉ ⊙ sign ( e i ) , sign ( x ) , x < 0 \Delta=\bar{\Delta} \odot \operatorname{sign}\left(e_{i}\right), \operatorname{sign}(\mathrm{x}), x<0 Δ=Δˉ⊙sign(ei),sign(x),x<0则输出-1,否则1。 Δ ˉ ∼ U ( 0 , 1 ) \bar{\Delta} \sim U(0,1) Δˉ∼U(0,1)。因此这两个扰动可以看作在原始embedding的方向,各自伸缩了一些。然后带入对比学习loss,就可以用了。
在实现上就更简单暴力了,只是在每层embedding加扰动而已:
E ′ = 1 L ( ( A ~ ( 0 ) + Δ ( 1 ) ) + ( A ~ ( A ~ E ( 0 ) + Δ ( 1 ) ) + Δ ( 2 ) ) ) + … + ( A ~ L E ( 0 ) + A ~ L − 1 Δ ( 1 ) + … + A ~ Δ ( L − 1 ) + Δ ( L ) ) ) \begin{array}{r} \mathbf{E}^{\prime}=\frac{1}{L}\left(\left(\tilde{\mathbf{A}}^{(0)}+\Delta^{(1)}\right)+\left(\tilde{\mathbf{A}}\left(\tilde{\mathrm{A}} \mathrm{E}^{(0)}+\Delta^{(1)}\right)+\Delta^{(2)}\right)\right)+\ldots \\ \left.+\left(\tilde{\mathbf{A}}^{L} \mathbf{E}^{(0)}+\tilde{\mathbf{A}}^{L-1} \Delta^{(1)}+\ldots+\tilde{\mathbf{A}} \Delta^{(L-1)}+\Delta^{(L)}\right)\right) \end{array} E′=L1((A~(0)+Δ(1))+(A~(A~E(0)+Δ(1))+Δ(2)))+…+(A~LE(0)+A~L−1Δ(1)+…+A~Δ(L−1)+Δ(L)))
边栏推荐
- W5500通过上位机控制实现调节LED灯带的亮度
- W5500多节点连接
- Miidock Brief
- 小程序image 无法显示base64 图片 解决办法 有效
- Hardware connection server TCP communication protocol gateway
- LeetCode第303场周赛(20220724)
- Teach you how to configure S2E as the working mode of TCP client through MCU
- 【无标题】
- Hardware peripherals =maixpy3
- 已解决 Files‘ name is invalid or does not exist (1205)
猜你喜欢

Oil monkey script link

W5500上传温湿度到oneNET平台
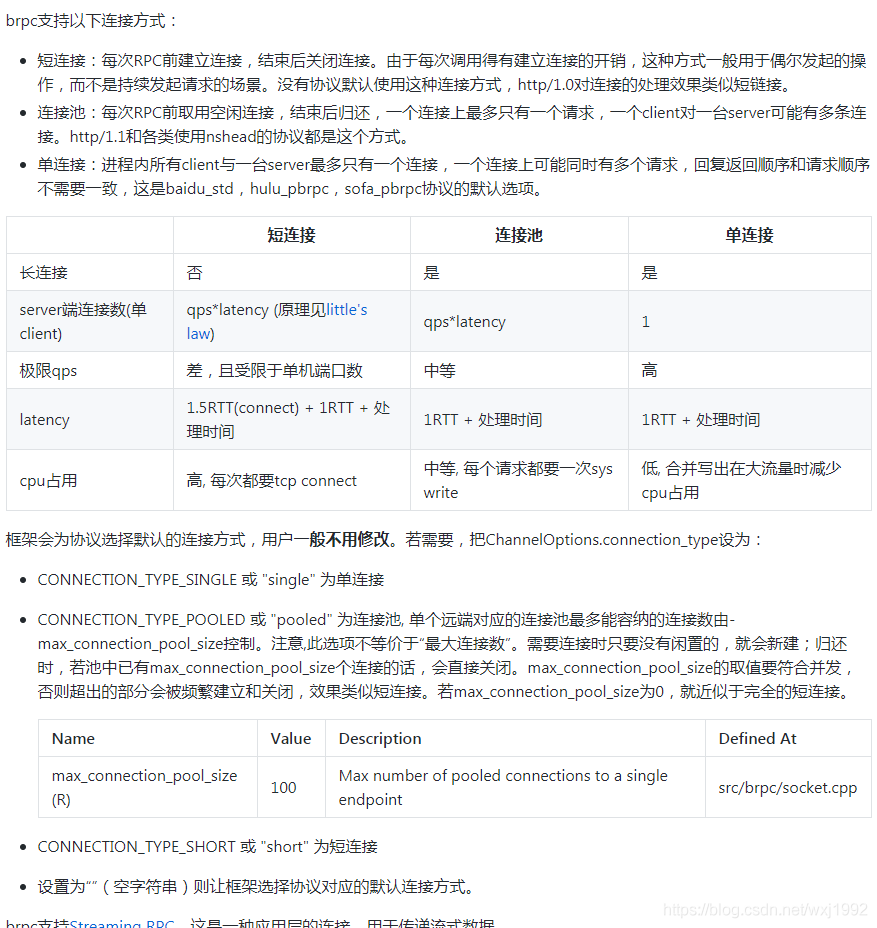
brpc源码解析(三)—— 请求其他服务器以及往socket写数据的机制

MIIdock简述

教你如何通过MCU配置S2E为TCP Client的工作模式

Functions in JS

Similarity matrix, diagonalization condition

Solutions to the failure of winddowns planning task execution bat to execute PHP files

11. Reading rumors spread with deep learning

剑指 Offer 22. 链表中倒数第k个节点
随机推荐
JaveScript循环
brpc源码解析(四)—— Bthread机制
Brpc source code analysis (VII) -- worker bthread scheduling based on parkinglot
Similarity matrix, diagonalization condition
W5500在处于TCP_Server模式下,在交换机/路由器网络中无法ping通也无法通讯。
"Mqtt protocol explanation and Practice (access to onenet)" of wiznet w5500 series training activities
剑指 Offer 22. 链表中倒数第k个节点
[MySQL 17] installation exception: could not open file '/var/log/mysql/mysqld log‘ for error logging: Permission denied
Flinksql client connection Kafka select * from table has no data error, how to solve it?
Qin long, a technical expert of Alibaba cloud: a prerequisite for reliability assurance - how to carry out chaos engineering on the cloud
Web APIs (get element event basic operation element)
【多模态】《TransRec: Learning Transferable Recommendation from Mixture-of-Modality Feedback》 Arxiv‘22
JS流程控制
Layout management ==pyqt5
PHP one server sends pictures to another. Curl post file_ get_ Contents save pictures
【多模态】《HiT: Hierarchical Transformer with Momentum Contrast for Video-Text Retrieval》ICCV 2021
brpc源码解析(五)—— 基础类resource pool详解
30套中国风PPT/创意PPT模板
dirReader. Readentries compatibility issues. Exception error domexception
Wiznet embedded Ethernet technology training open class (free!!!)