Geospatial search: implementation principle of KD tree

Previous review ：

Suppose we now have a data set , When given a new instance , The simplest and crudest way is to calculate its distance from all points , And then find k The nearest neighbor , Finally, judge the class of this instance according to the rule of majority voting .

But if there are many and intensive training examples in this dataset , And an instance has many features , Then you have to calculate thousands of distances , The amount of computation is extremely huge .

At this time , We can use a faster calculation method ——kd Trees .

What is? kd Trees

kd Trees look fundamentally , It's a binary tree structure , According to this structure k Continuous division of dimensional space , Each node represents k Dimension super rectangle area .

A two-dimensional （k=2） The rectangular area of ：

The three dimensional （k=3） The rectangular area of ：

Be careful ,kd The tree here k Represents the number of features , That is, the dimension of data , and k In the neighborhood k It refers to the closest to the new instance point k A neighbor .

How to construct kd Trees

principle

Input ： k Dimensional data sets ：

xi=(xi(1),xi(2),...,xi(k))T,xi(l) The superscript of represents the th l Eigenvalues

Output ： kd Trees

1. Start ： Construct the root node .

Select an optimal feature at the root node for cutting , It is generally determined by comparing the variance of each feature , The feature with the largest variance is what we want to choose Axis .

If we choose x(1), Take it as the coordinate axis , Find the syncopation point , Cut the super rectangular area into two sub areas . Usually selected x(1) The median of the data in the direction is used as the cut-off point , The depth generated from the root node is 1 Left and right child nodes of , The coordinates of the left node are smaller than the tangent point , The coordinate of the right node is greater than the tangent point .

2. repeat ： Selection and cutting of residual features

Continue to the depth of j The node of , choice x(1) Is the tangent axis ,l=j(mod k)+1, Take all instances in the node area x(1) The median of the coordinates is used as the tangent point , The region is continuously divided into two sub regions .

3. stop it ： obtain kd Trees

Stop segmentation until there are no instances in the two sub regions , That is to get a tree kd Trees .

Example explanation

Input ：

Output ： kd Trees

For convenience , Mark the data points in the data set for visual display ：

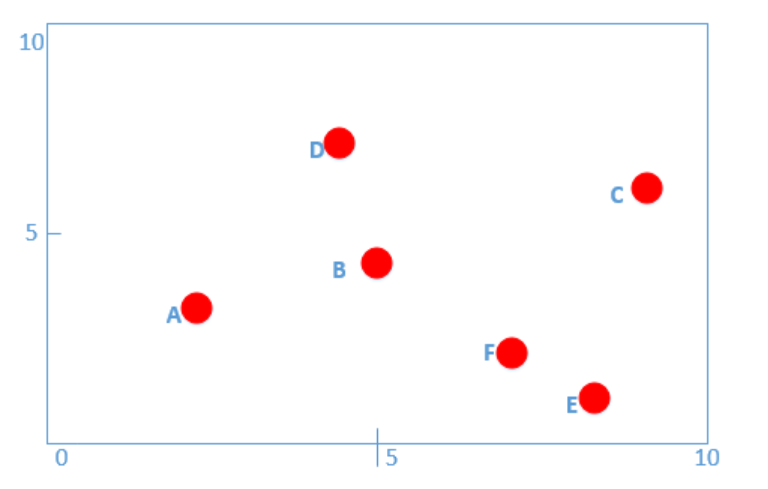
1. For the first time

Because the dimension of the training data set is 2, Then select any feature . Choose x(1) For the axis , take x(1) The data in is sorted from small to large , Namely ：2,4,5,7,8,9

The median might as well choose 7, namely With （7,2） Is the root node , Slice the whole area .

On the left is less than 7 The child node of , The one on the right is larger than 7 The child node of .

2. Second slice

Divide the area again ：

Add... To the first feature 1, With x(2) For the axis .

For the left area after the first segmentation , take x(2) The data in is sorted from small to large , Namely ：2,3,4,7

The median is 4, The coordinates of the syncopation point are  （5,4）, Draw another horizontal line for the second segmentation .

similarly , For the right area after the first segmentation , take x(2) The data in is sorted from small to large , Namely ：1,6

Because there are only two points , Choose 6 As a syncopation point , The coordinates of the tangent point in the right area are  （9,6） , Draw a horizontal line for the second segmentation .

3. Continue to cut

The second feature adds 1, With x(3) For the axis , And only here x(1) and x(2), So only for x(1) division . Or directly calculate 2(mod 2)+1=1 You can get the selected feature .

It's obvious that A（2,3）,D（4,7）,E（8,1）  The three instance points have not been segmented yet , Then take these points as root nodes and draw a line perpendicular to x(1) Cut the line of the axis .

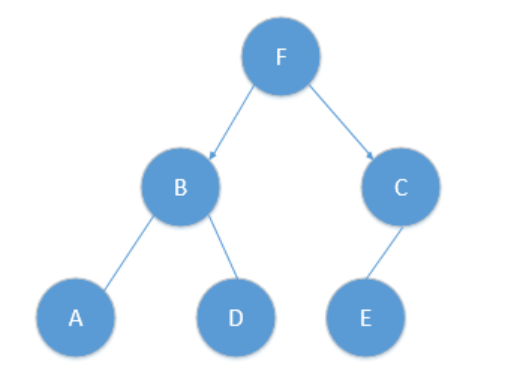
4. draw kd Trees

The root nodes in these divisions are ：

first stage ：（7,2）

Level second ：（5,4）,（9,6）

Level third ：（2,3）,（4,7）,（8,1）

Draw... According to this level kd Trees ：

How to search kd Trees

principle

Input ：  Constructed kd Trees , The target point is x

Output ： x The nearest neighbor of

seek “ The nearest point at the moment ”：  Starting from the root node , Recursive access kd Trees , Find out include x Leaf nodes of , This leaf node is “ The nearest point at the moment ”

to flash back ：  Take the target point and ” The nearest point at the moment “ Backtracking and iteration along the root of the tree , The current nearest point must exist in the region corresponding to a child node of the node , Check whether there is a closer point in the area corresponding to another child node of the parent node of the child node .

When you go back to the root node , End of the search , final ” The nearest point at the moment “ That is to say x The nearest neighbor of .

Example explanation

The tree generated above kd Trees, for example ：

Case 1

Input ： kd Trees , The target point x=(2.1,3.1)

Output ：  The nearest neighbor of the target

Find the nearest point ：  Start at root ,x=(2.1,3.1) At the root node （7,2） In the left sub region of , Continue to （5,4） In the determined left sub region , Continue to （2,3） In the right sub region of ,（2,3） Is the nearest neighbor .

to flash back ：  With （2.1,3.1） For the center of a circle , Draw a circle with its distance from the determined nearest neighbor as the radius , There are no other points in this area , That proves （2,3） yes （2.1,3.1） The nearest neighbor of .

Case 2

Input ： kd Trees , The target point x=（2,4.5）

Output ：  The nearest neighbor of the target point

Find the nearest point ：  Start at root ,x=（2,4.5） At the root node （7,2） In the left sub region of , Continue to （5,4） Within the determined upper sub region , Continue to （4,7） In the left sub region of ,（4,7） Is the nearest neighbor .

to flash back ：  We use （2,4.5） For the center of a circle , With （2,4.5） To （4,7） The distance between two points draws a circle for the radius , There are two nodes in this area , Namely （2,3） and （5,4）, By calculation （2,4.5） The distance to these two points , Come to （2,3） The closest , that （2,3） Is the nearest point . Then with （2,4.5） For the center of a circle , With （2,4.5） To （2,3） The distance between two points draws a circle for the radius , There are no other nodes in the circle , The description can confirm （2,3） Namely （2,4.5） The nearest neighbor of .