当前位置:网站首页>深度学习基本概念
深度学习基本概念
2022-07-31 11:53:00 【sweetheart7-7】
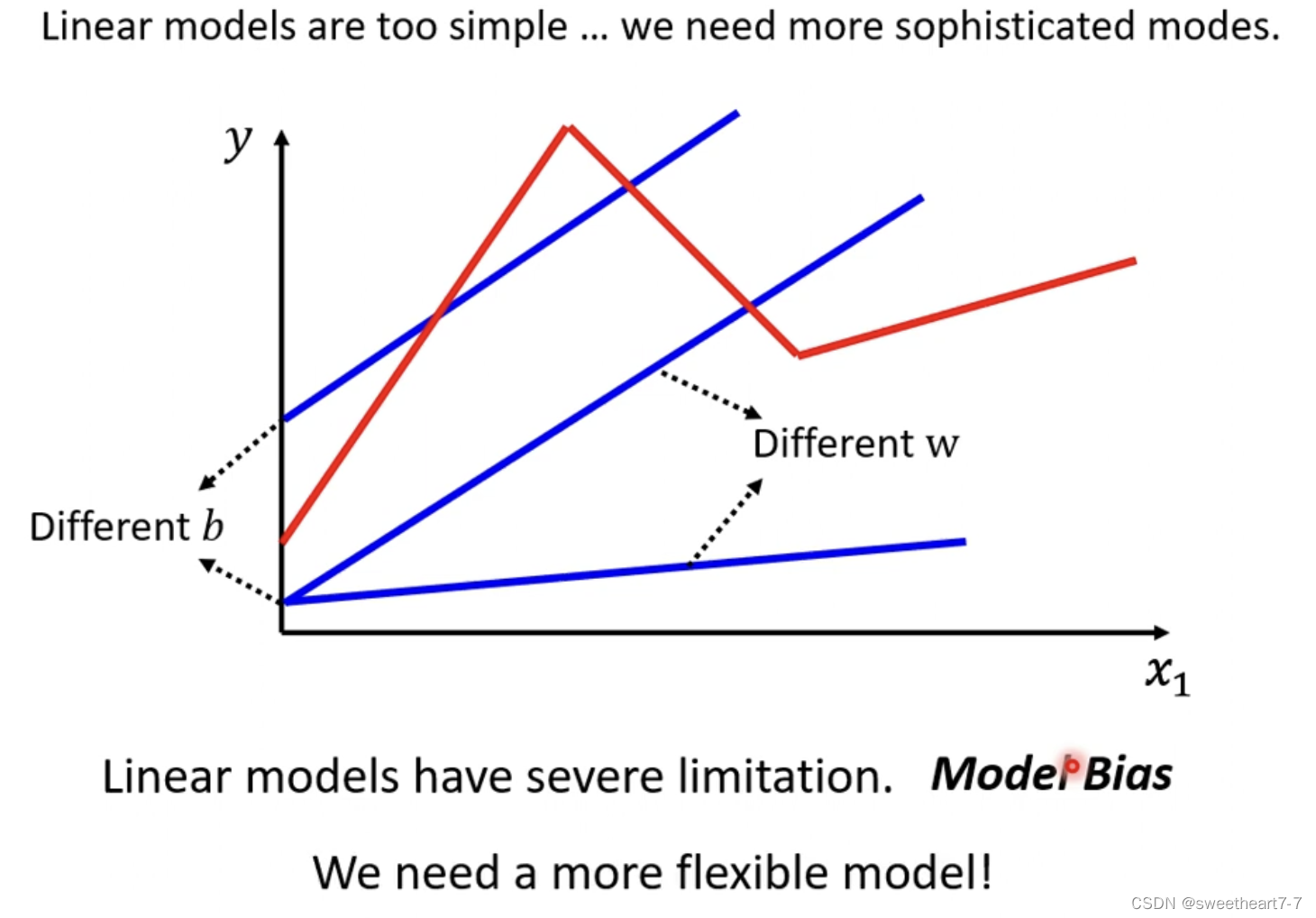
Liner Model 太过简单,不能拟合复杂的关系
可能出现如下情况:
如何写更复杂的有未知参数的函数?
红色function 可以看作 一个常数 + 一群蓝色的function
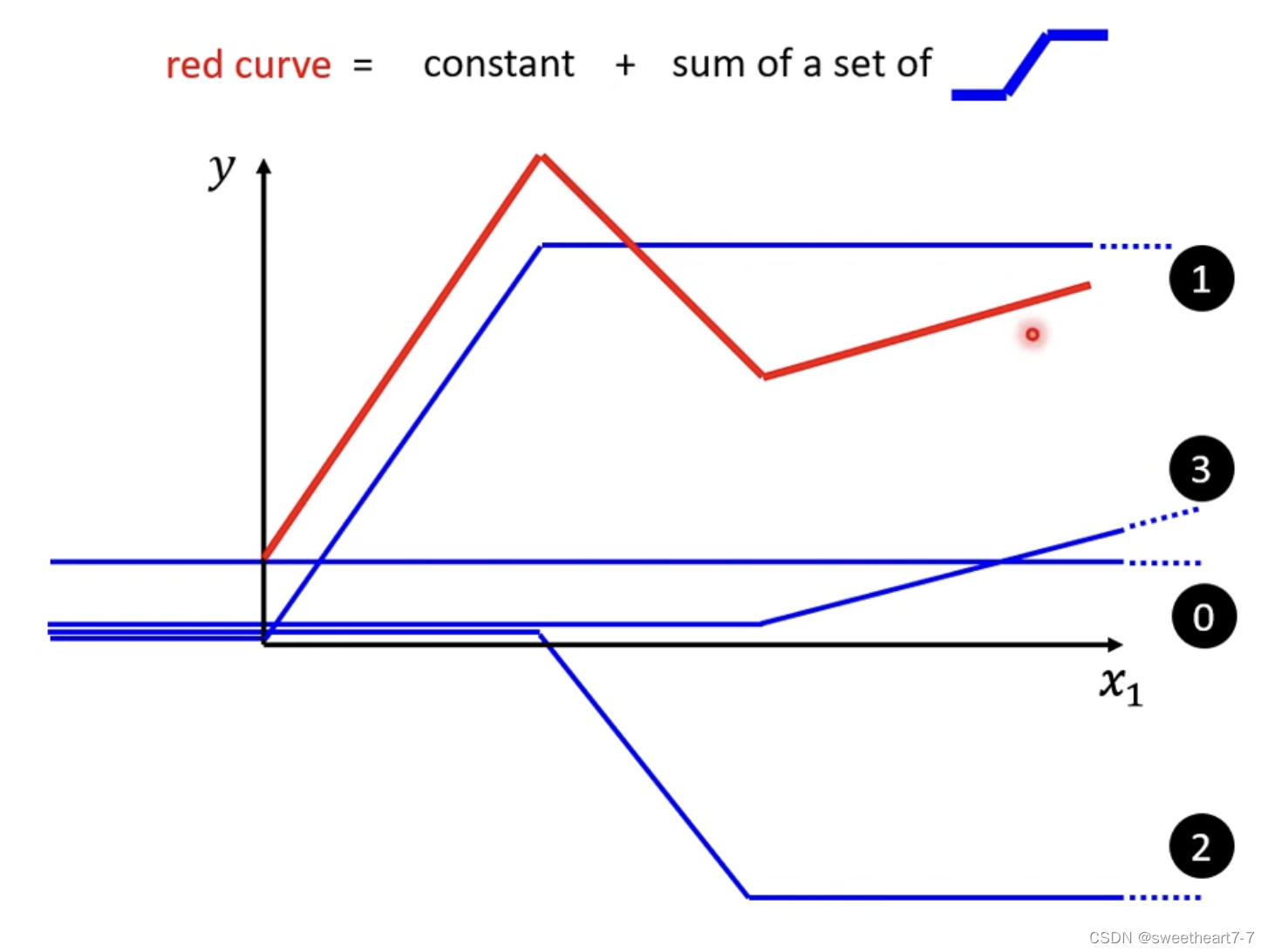
曲线也可以通过取适当的点然后把这些点连接起来形成一个 Piecewise Liner(分段) 的 Curves,所以可以通过足够多的 蓝色的 function 加起来形成任何的曲线。

通过 sigmoid function 来逼近 蓝色的 function
sigmoid Function:S 形的 function
y = c 1 1 + e − ( b + w x 1 ) y = c \frac{1}{1 + e^{-(b+wx_1)}} y=c1+e−(b+wx1)1
= c s i g m o i d ( b + w x 1 ) = c ~sigmoid(b+wx_1) =c sigmoid(b+wx1)
当 w w w 为正时, x 1 x_1 x1 趋近于 ∞ 时,sigmoid 趋近于 c c c, w w w 为负时,…,sigmoid 趋近于 0 0 0。

通过调整 w w w、 b b b 和 c c c 来得到各种形状的 sigmoid function 来拟合各种蓝色的 function。
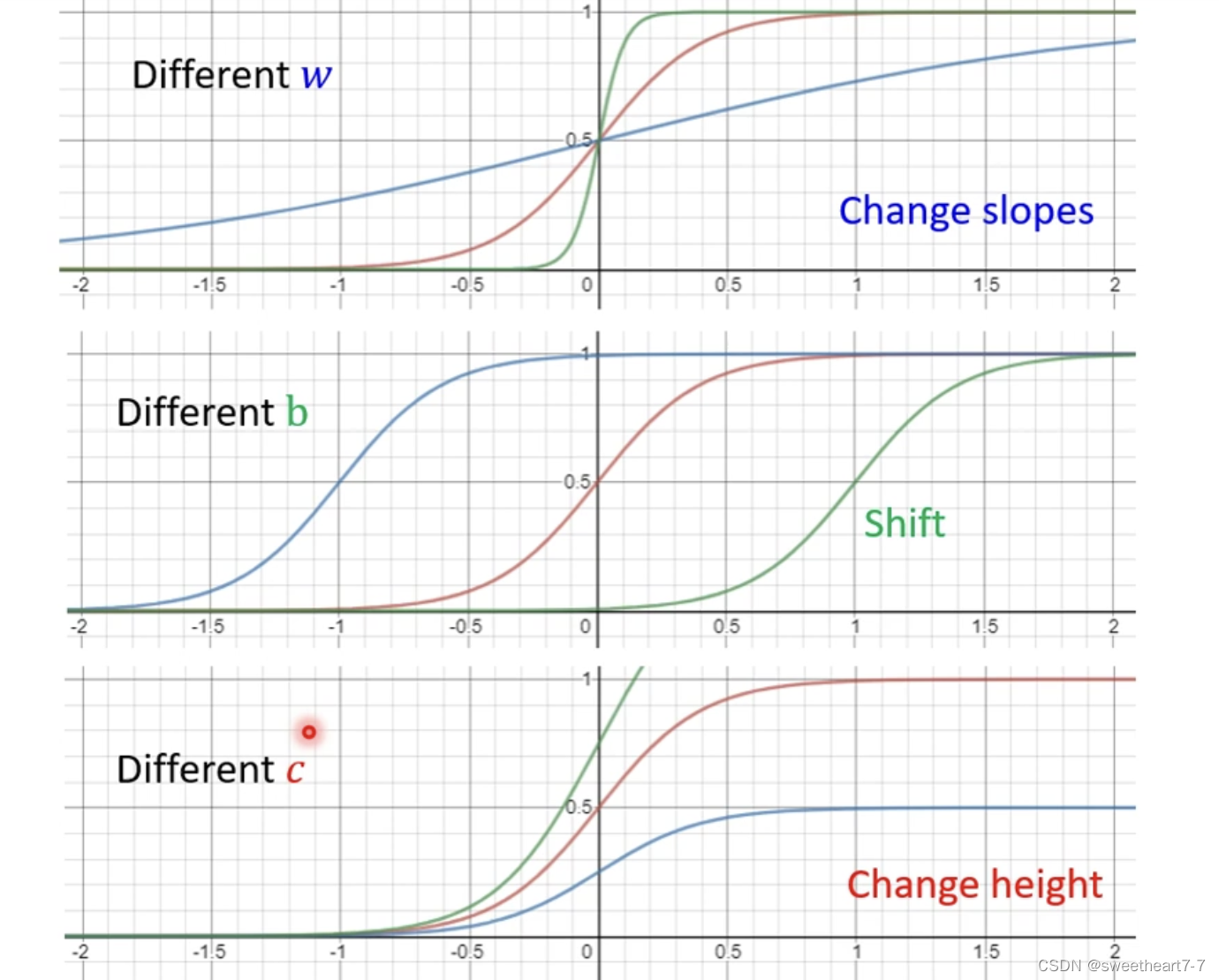
所以 0、1、2、3 这 4 条蓝色的 function 都可以用 c s i g m o i d ( b + w x 1 ) c sigmoid(b + wx_1) csigmoid(b+wx1) 来表示,只是对应的 c c c、 w w w 和 b b b 不同,所以红色的 function y y y 就可以用以下形式表示:

所以可以通过 调整 c i c_i ci、 b i b_i bi 和 w i w_i wi 来拟合各种各样曲线的 function
有弹性的有未知参数 function
从 线性的 y = b + w x 1 y=b + wx_1 y=b+wx1
推广到 分段 曲线 function
y = b + ∑ i c i s i g m o i d ( b i + w i + x 1 ) y = b + \sum_{i}c_i~sigmoid(b_i+w_i+x_1) y=b+∑ici sigmoid(bi+wi+x1)
这里只有 x 1 x_1 x1 代表只能通过当前一条数据结果来预测下一个结果。
而 在上一个 blog 最后 推广到可能具有周期性,所以可以通过 多个 feature 来改造函数,然后再对具有多个 feature 的函数进行推广,就有
y = b + ∑ j w j x j y = b + \sum_{j}w_jx_j y=b+∑jwjxj 推广为
y = b + ∑ i c i s i g m o i d ( b i + ∑ j w i j x j ) y = b + \sum_{i}c_i~sigmoid(b_i+\sum_{j}w_{ij}x_j) y=b+∑ici sigmoid(bi+∑jwijxj)
相当于从多个 feature 与 y y y 有一个线性关系推广为多个 feature 与 y y y 有一个曲线关系

i i i 代表多个 s i g m o i d 函数 sigmoid函数 sigmoid函数,而 j j j 代表多个feature
w i j w_{ij} wij 表示 再 第 i i i 个 sigmoid 里面乘 给 第 j j j 个 feature 的 w e i g h t weight weight
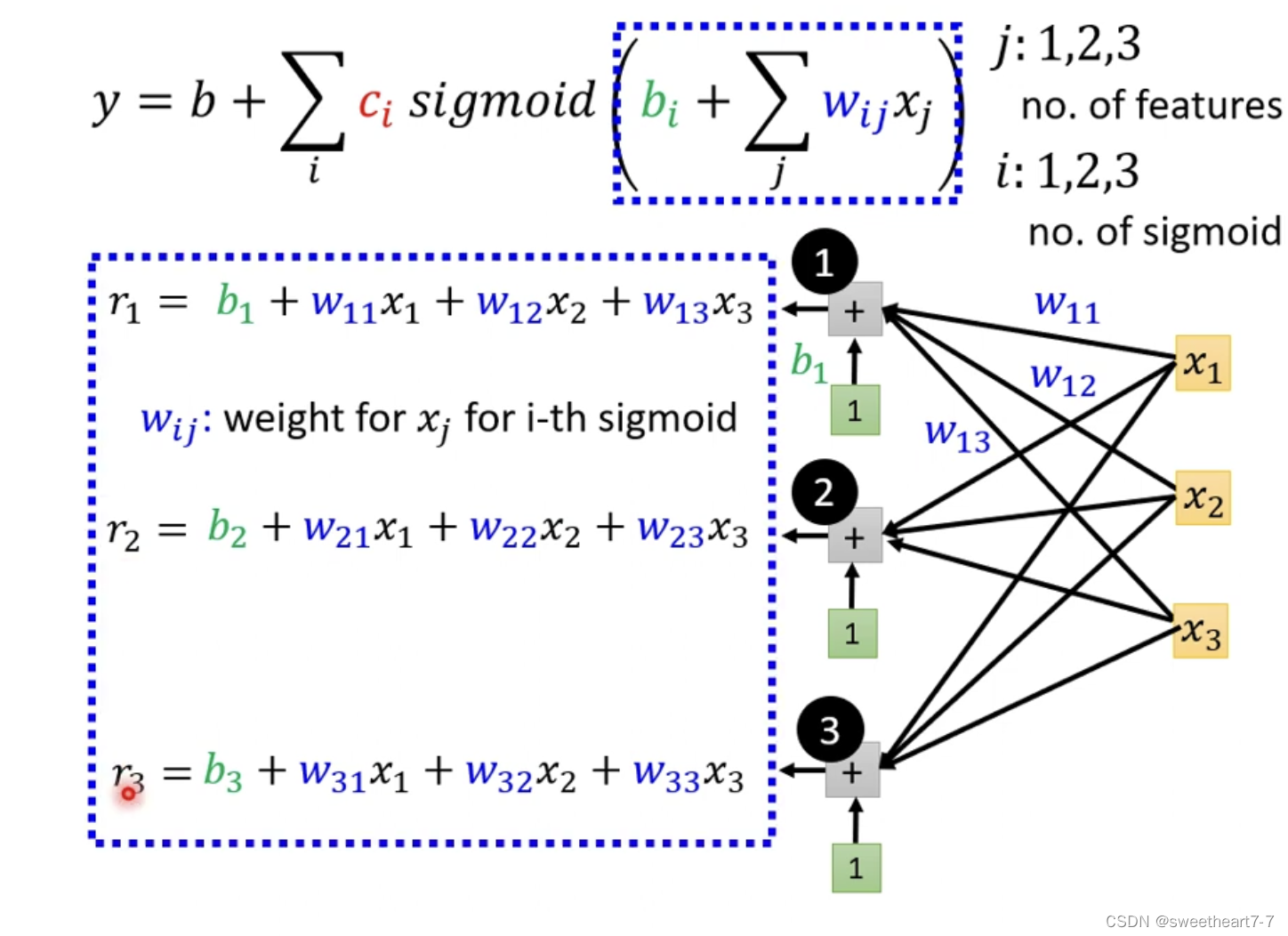
可以用以下向量与矩阵关系表示这个乘法关系

所以 a 1 = s i g m o i d ( r 1 ) = 1 1 + e − r 1 a_1 = sigmoid(r_1) = \frac{1}{1+e^{-r_{1}}} a1=sigmoid(r1)=1+e−r11
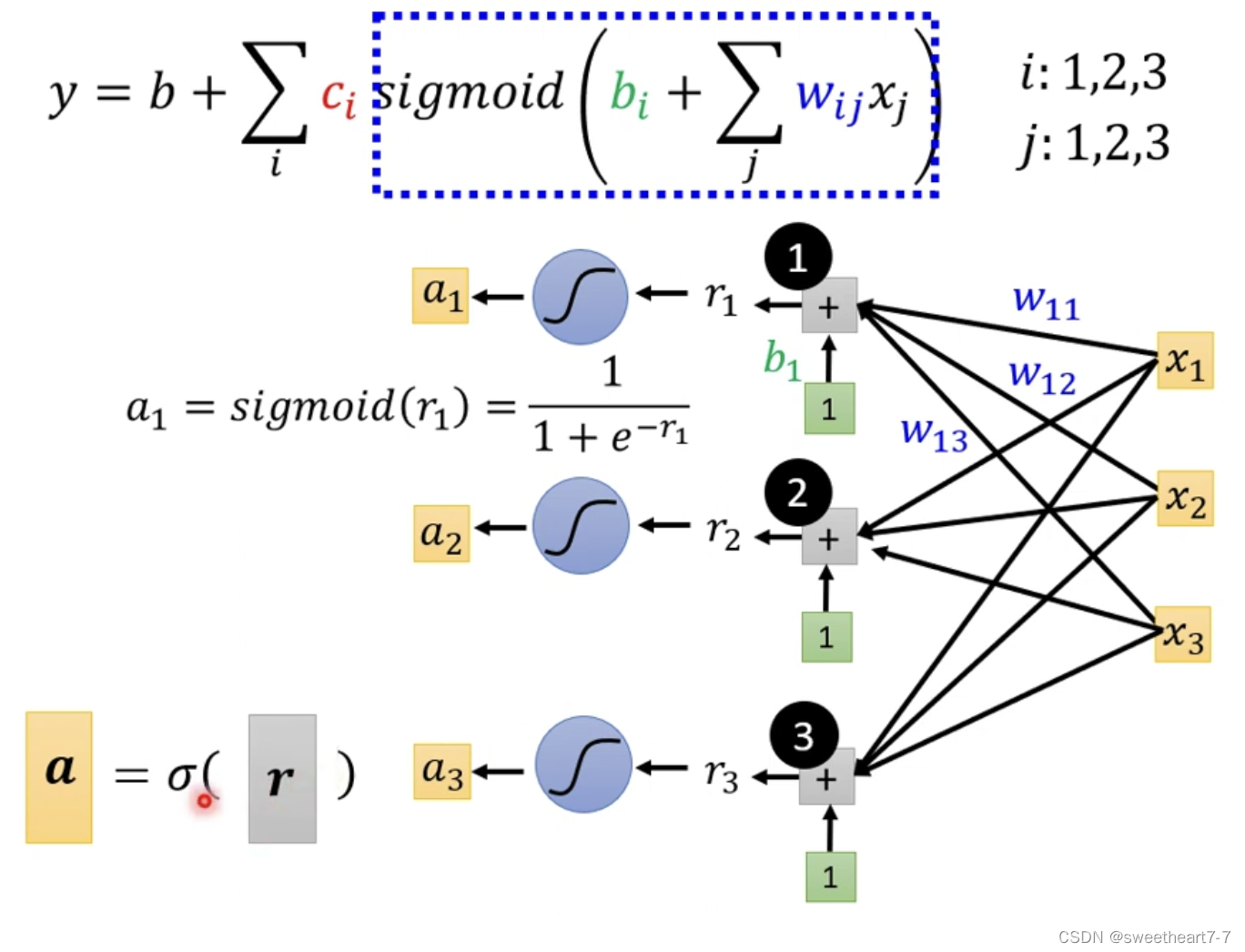
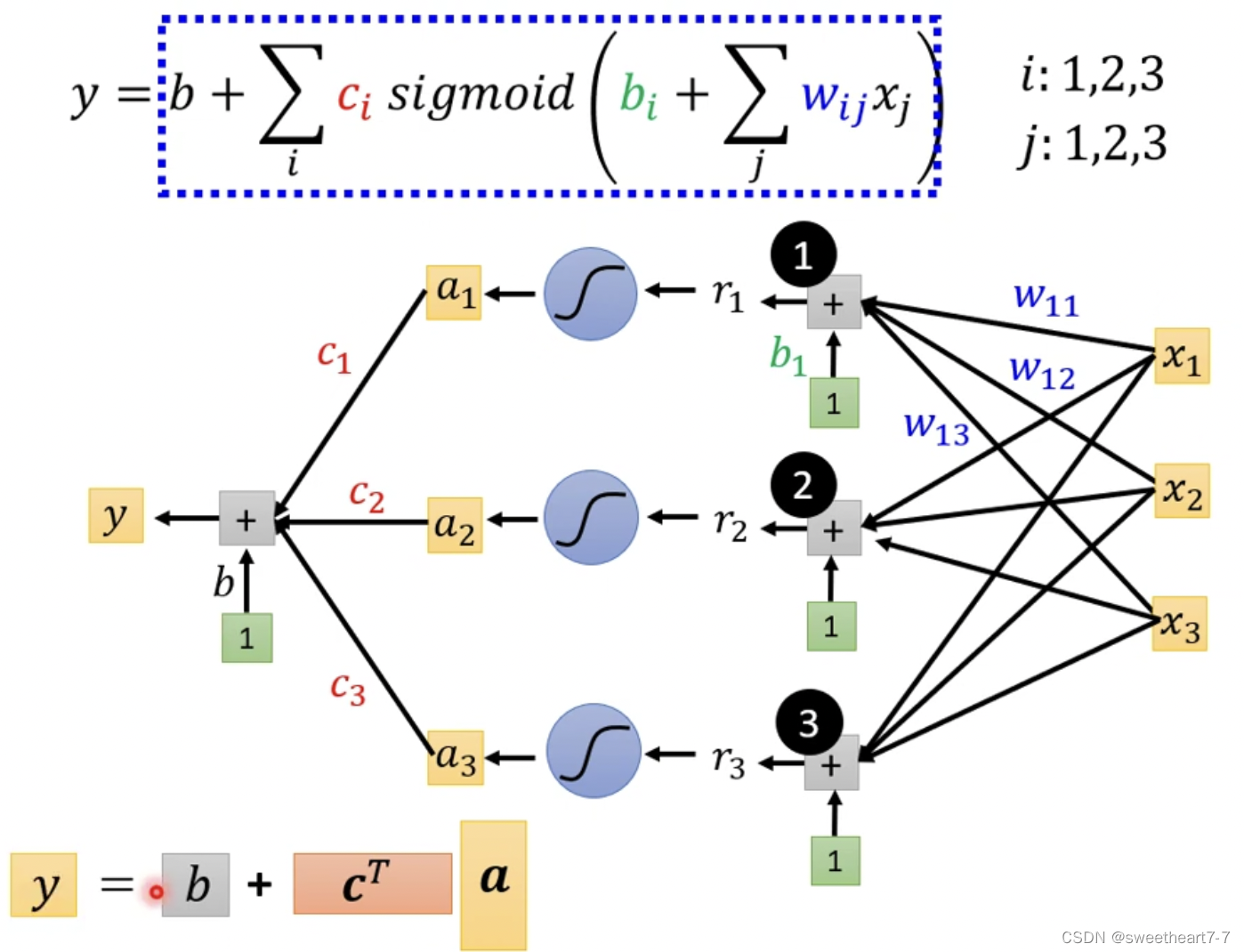
所以用线性代数表示为: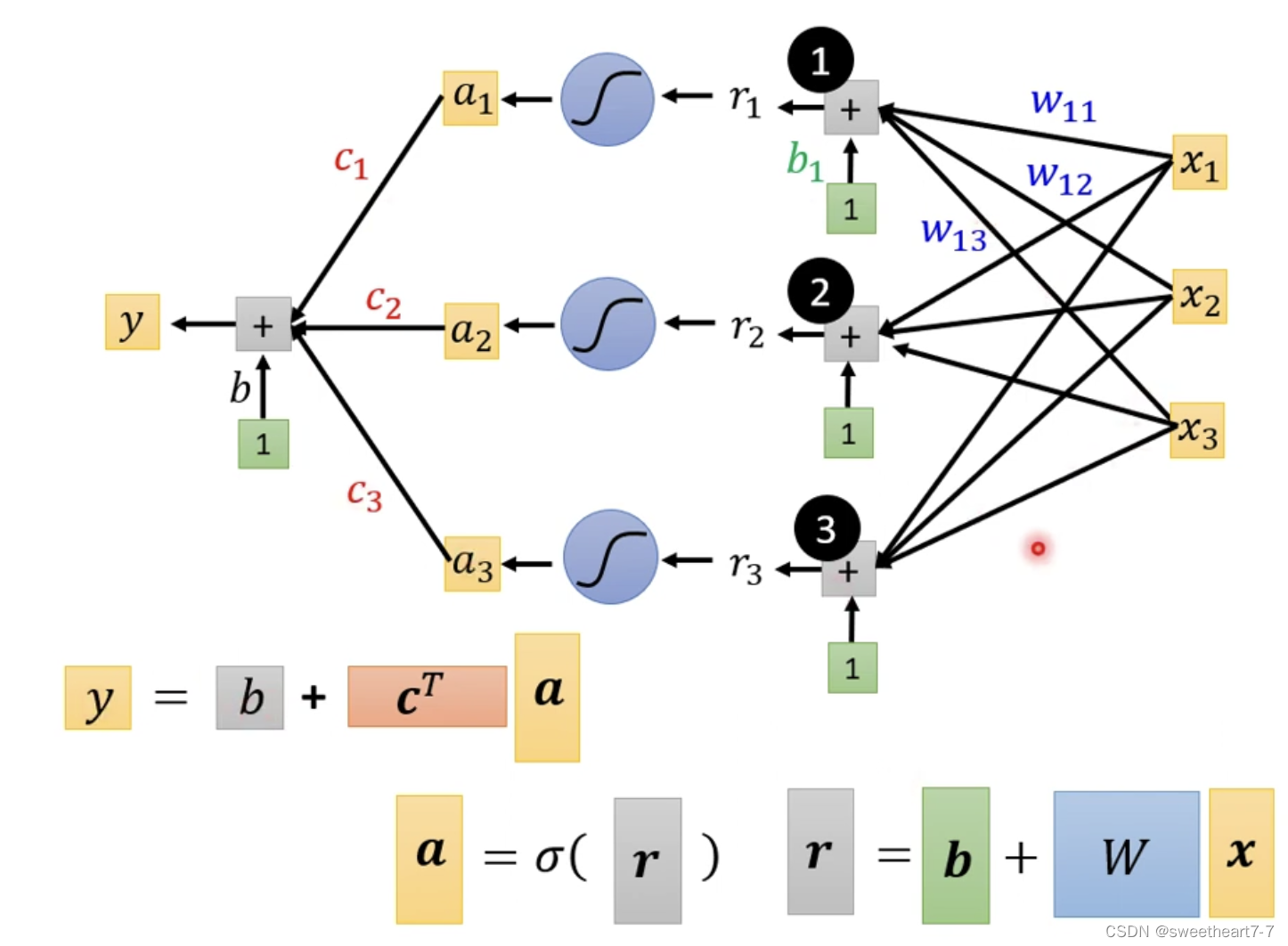
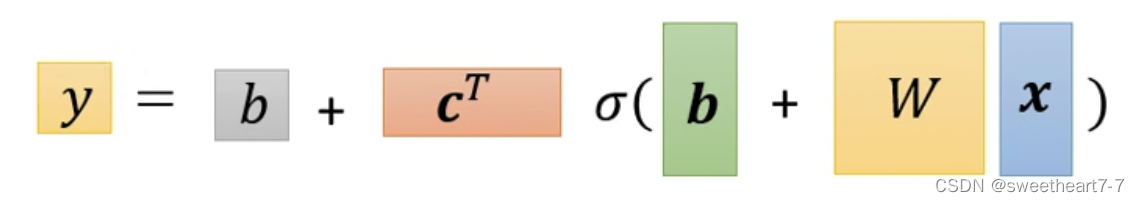
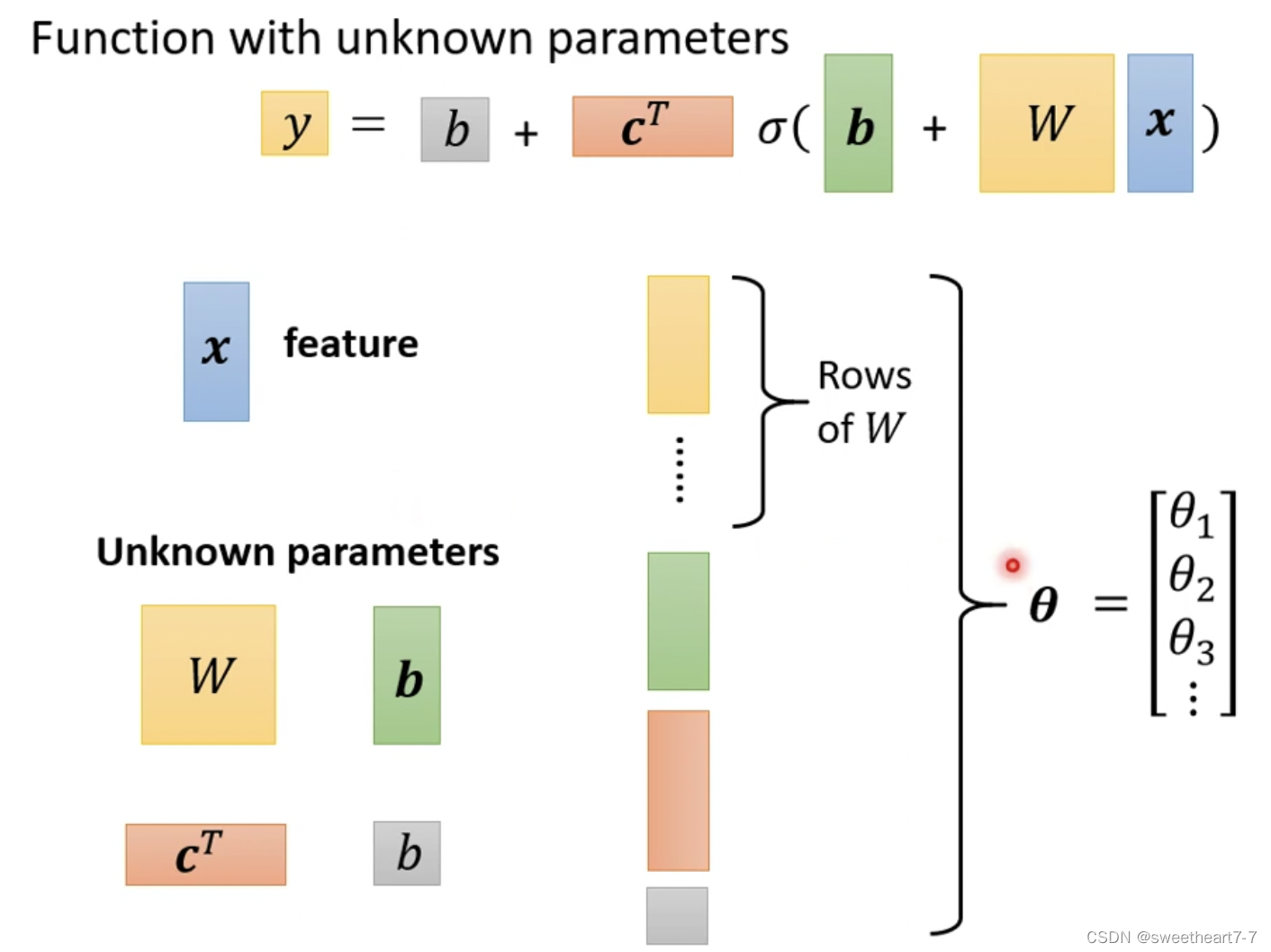
将未知参数 W W W、 b 向量 b向量 b向量、 C T 向量 C^T向量 CT向量、 b 常数 b常数 b常数展开成 θ θ θ 向量
这样就完成了 ML 的第一步
Loss 还是同样的方法,带入一组 θ θ θ 然后求得 y y y 并且求与 y ^ \hat{y} y^ 的差值,来判断这组 θ θ θ 的好坏。

第三步 Optimization 的方法也没有变化
对所有的 θ i θ_i θi 求 微分,然后得到一个向量 g g g
g g g 就是 gradient


在实际的程序中,需要把大 data 随机分成多个 batch,然后对每一个 batch 进行计算 g g g,更新 θ θ θ(一个 epoch),每一次更新参数(一个batch)叫做一次 update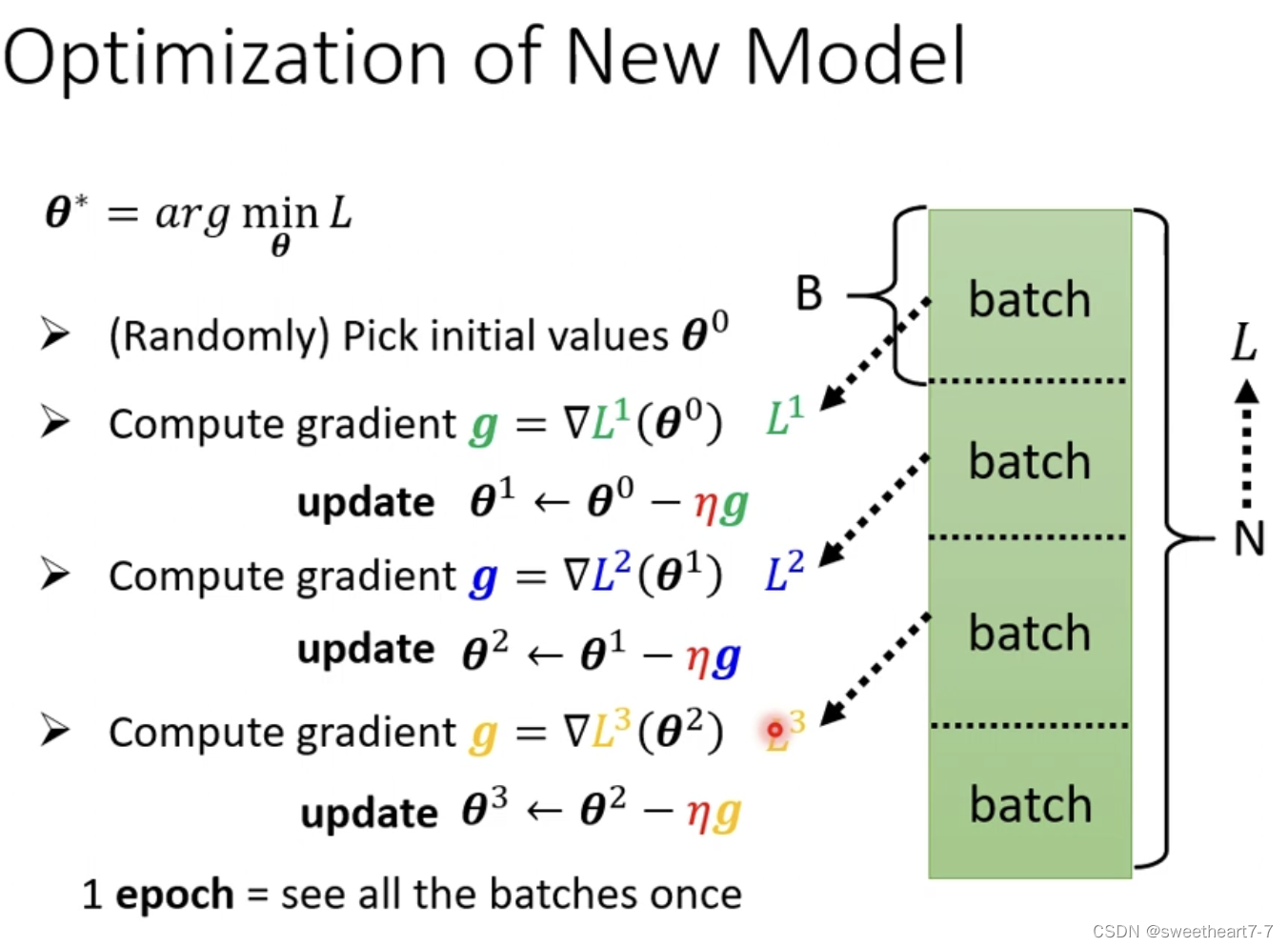
batchsize 也是 hyperparameter

通过 Relu 来逼近 蓝色的 function
需要先用 Relu 拟合 Hard sigmoid
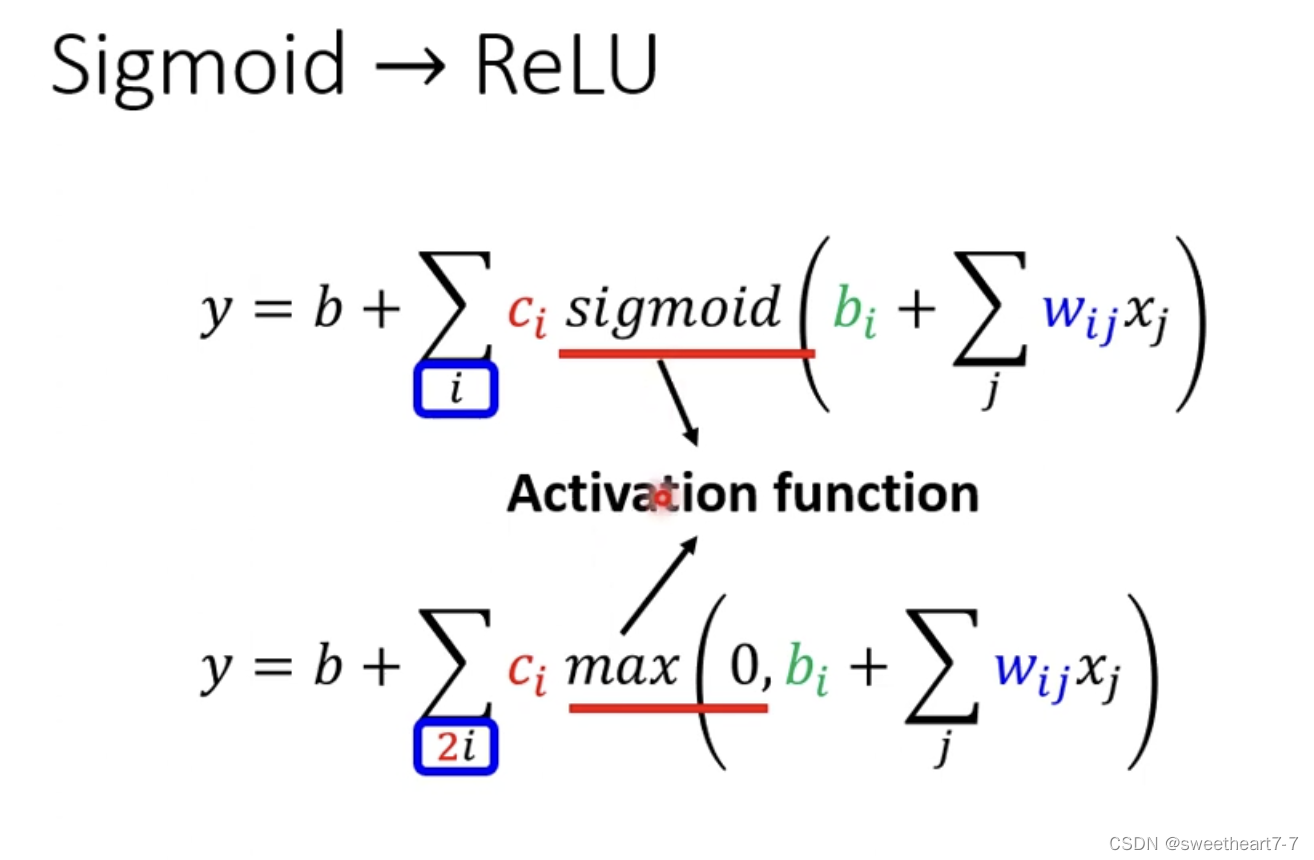
sigmoid 与 Relu 统称为 activation function
我们可以重复多次 进行如下扩展:

多个 layer



边栏推荐
- cesium-Web网页优化进阶
- JVS低代码能力简介及功能清单
- 【核心概念】图像分类和目标检测中的正负样本划分以及架构理解
- Docker installs canal and mysql for simple testing and achieves cache consistency between redis and mysql
- “带薪划水”偷刷阿里老哥的面经宝典,三次挑战字节,终成正果
- MySQL limit paging query and performance issues
- mysql automatically adds creation time and update time
- Different lower_case_table_names settings for server ('1') and data dictionary ('0') solution
- 使用 Excel 读取 SAP ABAP CDS View 通过 ODBC 暴露出来的数据
- vb.net 画曲线
猜你喜欢
随机推荐
Threading(in thread main)
CameraToolUnity中两种摄像机的两种观察控制方式
keras自带数据集(横线生成器)
【软件工程之美 - 专栏笔记】33 | 测试工具:为什么不应该通过QQ/微信/邮件报Bug?
CWE4.8 -- 2022年危害最大的25种软件安全问题
最全phpmyadmin漏洞汇总
MySQL row-level locks (row locks, adjacent key locks, gap locks)
最近两个月谷歌 ad 掉的厉害
第十二章 使用中的 OpenAPI 属性
Distributed Transactions - Introduction to Distributed Transactions, Distributed Transaction Framework Seata (AT Mode, Tcc Mode, Tcc Vs AT), Distributed Transactions - MQ
连续变量离散化教程
生信周刊第38期
oracle优化:instr做join条件很慢「建议收藏」
file contains vulnerabilities
「R」使用ggpolar绘制生存关联网络图
台达PLC出现通信错误或通信超时或下载时提示机种不符的解决办法总结
502 bad gateway causes and solutions
数据持久化技术——MP
关于==和equals的区别和联系,面试这么回答就可以
给你一个大厂面试的机会,你能面试上吗?进来看看!