NowCoderTOP28-34 binary tree - continuous update ing

TOP28. 二叉树的最大深度

public class Solution {
    
    /** * @param root TreeNode类 * @return int整型 */
    public int maxDepth (TreeNode root) {
    
        // In-order traversal computes depth
        int count = 0;
        if(root == null) return 0;
        // 队列
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        while(!queue.isEmpty()) {
    
            int size = queue.size();
            for(int i = 0; i < size ; i++){
    
                TreeNode node = queue.poll();
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
            count++;
        }
        return count;
        
// // 递归法
// if(root == null) return 0;
// return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}

TOP29. 二叉树中和为某一值的路径(一)

public class Solution {
    
    /** * @param root TreeNode类 * @param sum int整型 * @return bool布尔型 */
    public boolean hasPathSum (TreeNode root, int sum) {
    
        // 层序遍历
        if(root == null) return false;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()) {
    
            TreeNode node = queue.poll();
            
            if(node.left == null && node.right == null && node.val == sum) {
    
                return true;
            }
            if(node.left != null) {
    
                node.left.val = node.val + node.left.val;
                queue.offer(node.left);
            }
            if(node.right != null) {
    
                node.right.val = node.val + node.right.val;
                queue.offer(node.right);
            }
        }
        return false;
    }
    
        
// // 前序遍历 递归法
// // 边界条件
// if(root == null) return false;
// // 左右节点为空 即为子节点,and the value is the given sum sum 返回true
// if(root.left == null && root.right == null && root.val == sum) {
    
// return true;
// }
// return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
// }
}

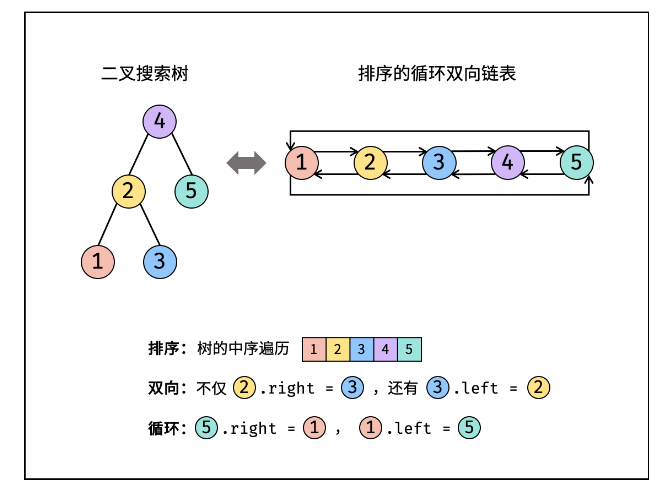
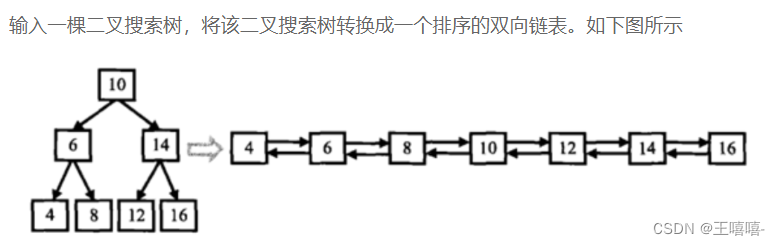
TOP30. 二叉搜索树与双向链表

public class Solution {
    
    // The first pointer returned is the minimum value,先定义为null
    public TreeNode head = null;
    // 中序遍历当前值的上一位,The initial value is the minimum value,先定为null
    public TreeNode pre = null;
    public TreeNode Convert(TreeNode pRootOfTree) {
    
        // 中序 Leaves are empty,则返回
        if(pRootOfTree == null) return null;
        // 首先递归到最左 最小值
        Convert(pRootOfTree.left);
        // 找到了 最小值,初始化 head 和 pre
        if(pre == null) {
    
            head = pRootOfTree;
            pre = pRootOfTree;
        }
        else{
    
            pre.right = pRootOfTree;
            pRootOfTree.left = pre;
            pre = pRootOfTree;
        }
        Convert(pRootOfTree.right);
        return head;
    }
}

TOP31. 对称的二叉树

public class Solution {
    boolean isSymmetrical(TreeNode pRoot) {
        // Empty trees are symmetric
        if(pRoot == null) return true;
        // Auxiliary queues are used for hierarchical traversal from both sides
        Queue<TreeNode> q1 = new LinkedList<TreeNode>();
        Queue<TreeNode> q2 = new LinkedList<TreeNode>();
        q1.offer(pRoot.left);
        q2.offer(pRoot.right);
        while(!q1.isEmpty() && !q2.isEmpty()) {
            // 分别从左边和右边弹出节点
            TreeNode left = q1.poll();
            TreeNode right = q2.poll();
            // 都为空 暂时对称
            if(left == null && right == null) continue;
            // 若有一个不为空,Or the elements are not equal,则不对称
            if(left == null || right == null || left.val != right.val) return false;
            // 从左往右加入队列
            q1.offer(left.left);
            q1.offer(left.right);
            // Join the queue from right to left
            q2.offer(right.right);
            q2.offer(right.left);
        }
        // all checked is symmetrical
        return true;
    }
}

TOP32. 合并二叉树

public class Solution {
    
    /** * * @param t1 TreeNode类 * @param t2 TreeNode类 * @return TreeNode类 */
    public TreeNode mergeTrees (TreeNode t1, TreeNode t2) {
    
        //若只有一个节点返回另一个,两个都为null自然返回null
        if(t1 == null) return t2;
        if(t2 == null) return t1;
        // 合并根节点
        TreeNode head = new TreeNode(t1.val + t2.val);
        // 连接后的树的层次遍历节点
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        // 分别存两棵树的层次遍历节点
        Queue<TreeNode> q1 = new LinkedList<TreeNode>();
        Queue<TreeNode> q2 = new LinkedList<TreeNode>();
        q.offer(head);
        q1.offer(t1);
        q2.offer(t2);
        while(!q1.isEmpty() && !q2.isEmpty()) {
    
            TreeNode node = q.poll();
            TreeNode node1 = q1.poll();
            TreeNode node2 = q2.poll();
            
            TreeNode left1 = node1.left;
            TreeNode left2 = node2.left;
            
            TreeNode right1 = node1.right;
            TreeNode right2 = node2.right;
            
            if(left1 != null || left2 != null) {
    
                // Both nodes exist
                if(left1 != null && left2 != null) {
    
                    TreeNode left = new TreeNode(left1.val + left2.val);
                    node.left = left;
                    // 新节点 入 队列
                    q.offer(left);
                    q1.offer(left1);
                    q2.offer(left2);
                }// 只连接一个节点
                else if(left1 != null) node.left = left1;
                else node.left = left2;
            }
            if(right1 != null || right2 != null) {
    
                // 两个右节点都存在
                if(right1 != null && right2 != null) {
    
                    TreeNode right = new TreeNode(right1.val + right2.val);
                    node.right = right;
                    // 新节点入队列
                    q.offer(right);
                    q1.offer(right1);
                    q2.offer(right2);
                //只连接一个节点
                }else if(right1 != null) node.right = right1;
                 else node.right = right2;
                }
            }
        return head;
    }
    
        
// // 递归前序遍历
// //若只有一个节点返回另一个,两个都为null自然返回null
// if(t1 == null) return t2;
// if(t2 == null) return t1;
// TreeNode head = new TreeNode(t1.val + t2.val);
// head.left = mergeTrees(t1.left, t2.left);
// head.right = mergeTrees(t1.right, t2.right);
// return head;
// }
}

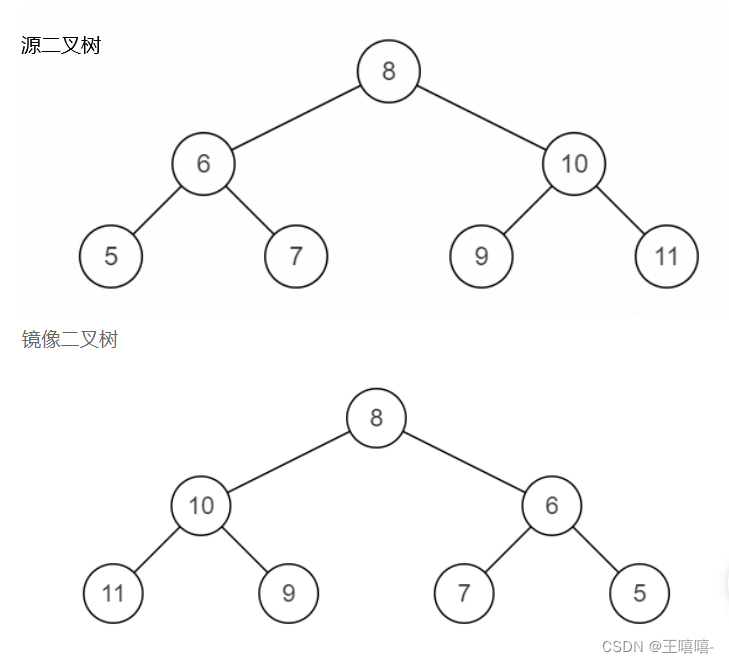
TOP33. 二叉树的镜像

public class Solution {
    
    /** * 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可 * @param pRoot TreeNode类 * @return TreeNode类 */
    public TreeNode Mirror (TreeNode pRoot) {
    
        // 递归实现
        if(pRoot == null) return null;
        // 交换
        TreeNode temp = pRoot.left;
        pRoot.left = pRoot.right;
        pRoot.right = temp;
        // 递归
        pRoot.left = Mirror(pRoot.left);
        pRoot.right = Mirror(pRoot.right);
        return pRoot;
    }
         
// // 辅助栈
// if(pRoot == null) return null;
// Stack<TreeNode> stack = new Stack<>();
// // 根节点入栈
// stack.add(pRoot);
// while(!stack.isEmpty()) {
    
// // 节点出栈
// TreeNode node = stack.pop();
// // The left and right subtrees of the root are pushed onto the stack
// if(node.left != null) stack.add(node.left);
// if(node.right != null) stack.add(node.right);
// // 左右子树交换
// TreeNode temp = node.left;
// node.left = node.right;
// node.right = temp;
// }
// return pRoot;
// }
}

TOP34. 判断是不是二叉搜索树

public class Solution {
    
    /** * 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可 * @param root TreeNode类 * @return bool布尔型 */
// int pre = Integer.MIN_VALUE;
    public boolean isValidBST (TreeNode root) {
    
        // First set up the stack for traversal
        Stack<TreeNode> stack = new Stack<TreeNode>();
        TreeNode head = root;
        // An array of records traversed in-order
        ArrayList<Integer> list = new ArrayList<Integer>();
        while(head != null || !stack.isEmpty()) {
    
            // 将左节点入栈,用来保存父问题,直到没有左节点
            while(head != null) {
    
                stack.push(head);
                head = head.left;
            }
            head = stack.pop();
            // 访问节点
            list.add(head.val);
            // 进入右边
            head = head.right;
        }
        // The result of the in-order traversal is accessed at this point
        for(int i = 0; i < list.size() - 1; i++) {
    
            if(list.get(i) > list.get(i + 1)) return false;
        }
        return true;
    }
        
            // 中序遍历
// if(root == null) return true;
// // 左子树
// if(!isValidBST(root.left)) return false;
// if(root.val < pre) return false;
// // 更新最值
// pre = root.val;
// // 再进入右子树
// return isValidBST(root.right);
// }
}