当前位置:网站首页>Task Computing【动态规划_牛客】
Task Computing【动态规划_牛客】
2022-08-04 15:36:00 【波风一一水门】
Task Computing
主要讲思考顺序。
"蔚来杯"2022牛客暑期多校训练营4
题意: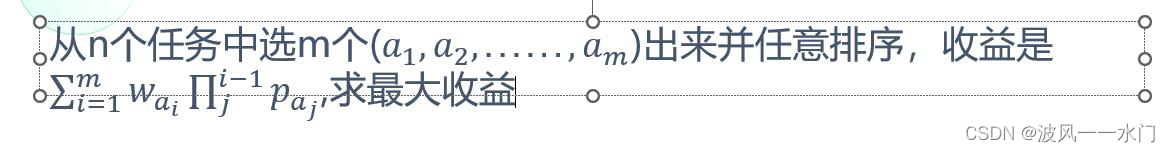
题解的图片丢了 j = 0 j = 0 j=0 下界。
5 2
1 2 3 4 5
12000 11000 10000 9000 8000
思路:首先考虑到式子中的 w a i ∗ ∏ j = 0 i − 1 p j w_{a_i}*\prod \limits_{j=0}^{i - 1}p_j wai∗j=0∏i−1pj ,当前选的物品价值 a i a_i ai会被后边的数乘起来。
所以如果按照原序列选择一个子序列作为答案的话,显然不能满足最优(因为题意选完之后可以任意排序)。
此时我们需要找到一种排列顺序,可以保证我按照此序列选出某个子序列之后,不会出现交换某两个数之后,使得答案变差。
这道题需要找到一种排列顺序,前提要先想清楚选取顺序,因为这道题动态规划的转移依赖于你排序的贪心策略,如果你让 x x x
排在 y y y 的前边更优,那么你的 y y y 一定是在 x x x 后边选取的,那么 y y y 的状态必须由 x x x 来转移,不然你排序排的就是寂寞!。
那么这道题我反过来排序——按照题解的顺序来讲。其实前一种已经很好考虑了。
那么我可以假设我把 x x x 排在 y y y 的“后边”得出的收益大于 把 y y y 排在 x x x 的“后边”的收益。这个不是字面意思“后边”,请看下去。
对于一个贪心策略的说明:如果按照某个假设的逻辑进行不等式推导,那么满足这个不等式的情况下就满足了原假设。
题解已经假设了一种结构,正在推导一个不等式。

这个题解的推导的 x x x 排在 y y y 的“后边” ,虽说在原序列中看似 x x x 是 在 y y y 的前边,但实则不然,原来题解早就想到这道题要倒着选取,所以它默认了 x x x 要在 y y y 的后边选!【本题核心】
明确了先选的状态推导或者后选的状态之后,那么我们考虑转移。
如果按照题解的推导顺序,我们 可以通过 如下转移: d p [ i ] [ k ] = d p [ i + 1 ] [ k − 1 ] ∗ p [ i ] + w [ i ] dp[i][k] = dp[i+1][k-1] * p[i] + w[i] dp[i][k]=dp[i+1][k−1]∗p[i]+w[i]。
为什么此时不去正向选取,因为首先正向考虑需要求出前一个状态的 ∏ j = 0 i − 1 p j \prod \limits_{j=0}^{i - 1}p_j j=0∏i−1pj ,这并不容易在转移中处理出来。但最重要的一点就是我们其实已经考虑到了选取顺序的问题是从后往前的,这件事我们在排序之前已经想清楚了,那么状态转移也一定是从后向前的,这个考虑方式正是自洽的,如果从头推到尾就不会出现考虑枚举顺序的问题。如果想清楚这件事,也就明白为什么与题解反过来排序就是从前往后的 d p dp dp 顺序了,可以试一下。这道题因我自身对于贪心策略的推导不熟练和枚举顺序的思路不清晰,以至于想了很久才想明白,以此记录一下。
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 10;
int n , ans , m ;
double dp[N][25];
struct node
{
double w , p;
}e[N];
bool cmp(node x , node y)
{
return x.w * (1 - y.p) > y.w * (1 - x.p);
}
signed main()
{
cin >> n >> m;
for(int i = 1 ; i <= n ; i ++)
{
scanf("%lf" , &e[i].w);
}
for(int i = 1 ; i <= n ; i ++)
{
double b;
scanf("%lf" , &b);
e[i].p = b / 10000.0;
}
sort(e + 1 , e + 1 + n , cmp);
for(int i = 1 ; i <= n + 1 ; i ++)
{
for(int j = 0 ; j <= m + 1; j ++)
dp[i][j] = -1e15;
}
for(int i = 1 ; i <= n + 1 ; i ++) dp[i][0] = 0;
for(int i = n ; i >= 1 ; i --)
{
for(int j = 0 ; j <= m ; j ++)
{
dp[i][j] = dp[i + 1][j];
if(j)
dp[i][j] = max(dp[i][j] , dp[i + 1][j - 1] * e[i].p + e[i].w);
}
}
printf("%0.7lf\n" , dp[1][m]);
}
边栏推荐
猜你喜欢

洛谷题解P1028 数的计算
The electromagnetic compatibility EMC protection study notes

性能提升400倍丨外汇掉期估值计算优化案例

我在羊毛和二手群里报复性消费
What are the useful IT asset management platforms?
remote: Check Access Error, please check your access right or username and password!fatal: Authenti
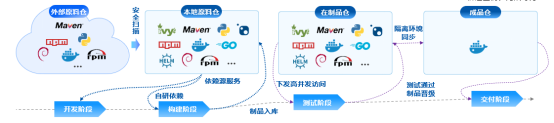
DevOps平台中的制品库是什么?有什么用处?
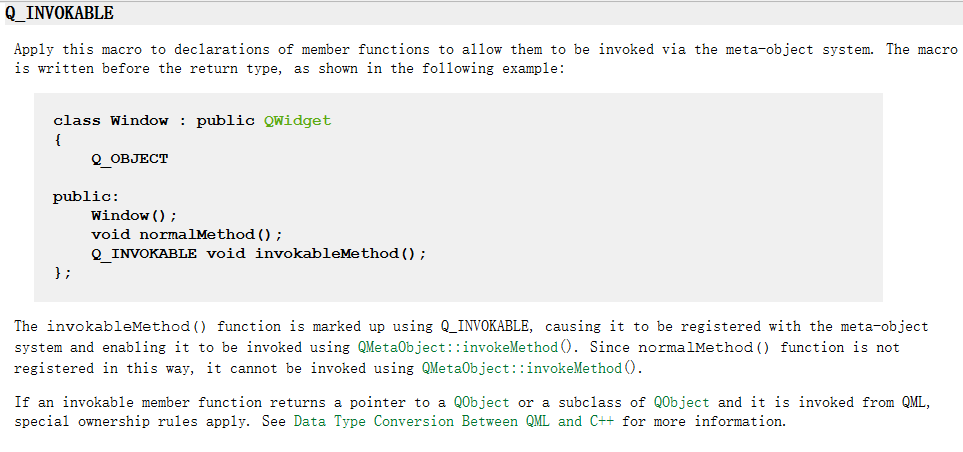
QT笔记——Q_INVOKABLE了解
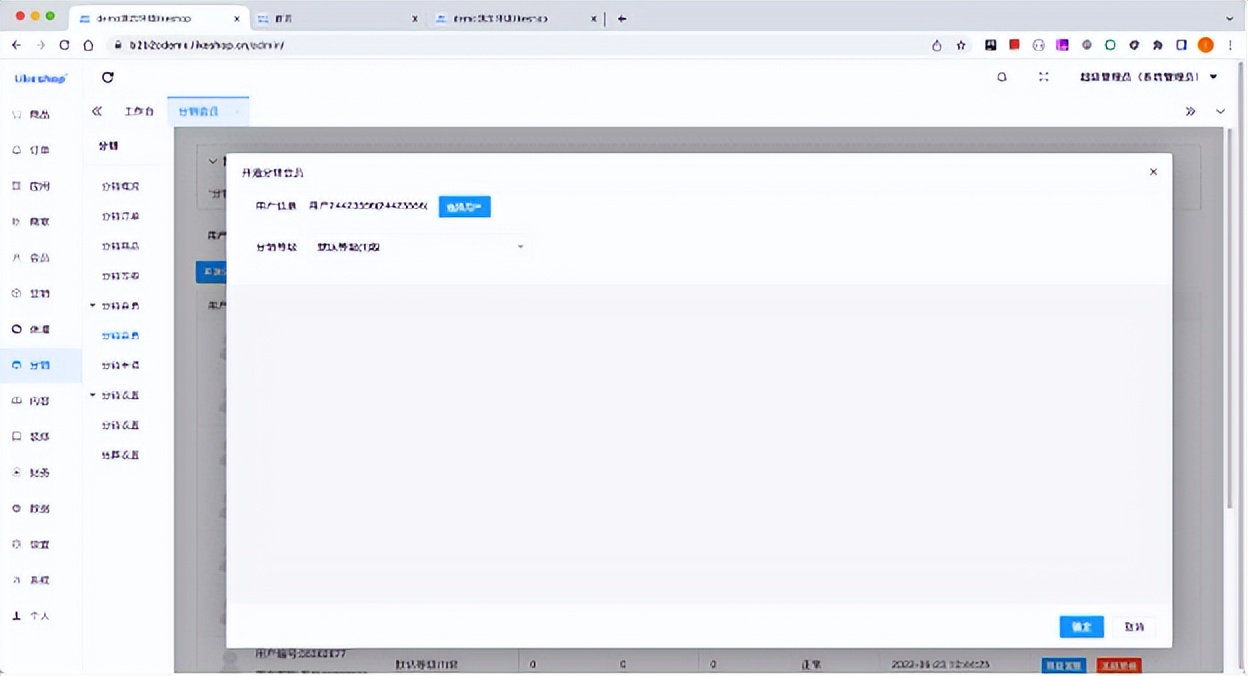
多商户商城系统功能拆解24讲-平台端分销会员
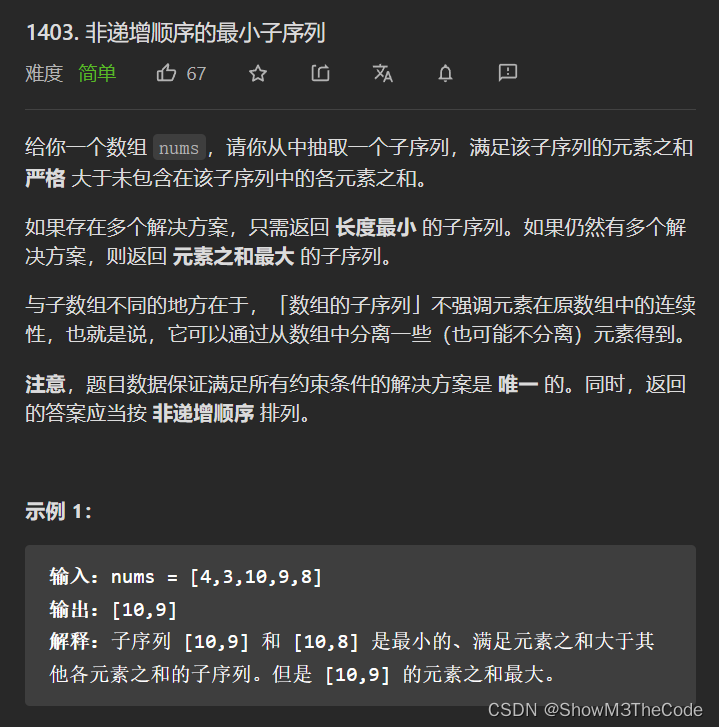
365天挑战LeetCode1000题——Day 049 非递增顺序的最小子序列 贪心
随机推荐
Byte、Short、Integer、Long内部缓存类的对比与源码分析
有哪些好用的IT资产管理平台?
聊聊与苹果审核员的爱恨情仇
Roslyn 节点的 Span 和 FullSpan 有什么区别
What are the useful IT asset management platforms?
【Harmony OS】【FAQ】Hongmeng Questions Collection 2
What is an artifact library in a DevOps platform?What's the use?
Go Go 简单的很,标准库之 fmt 包的一键入门
分支控制if-else
Manacher(求解最长回文子串)
OGG判断mgr状态并自动启动脚本
学 Go,最常用的技能是什么?打日志
Xi'an Zongheng Information × JNPF: Adapt to the characteristics of Chinese enterprises, fully integrate the cost management and control system
ICDE‘22推荐系统论文之Research篇
阿尔萨斯监控平台&普罗米修斯监控平台对服务器资源的监控
洛谷题解P4326 求圆的面积
FTP协议抓包-工具wireshark与filezilla
Projector reached the party benefits 】 【 beginners entry - brightness projection and curtain selection - from entry to the master
弄懂#if #ifdef #if defined
SublimeText 粘贴图片保存到本地