当前位置:网站首页>Data analysis - numpy quick start
Data analysis - numpy quick start
2022-06-26 16:11:00 【redrose2100】
【 Link to the original text 】
List of articles
- 【 Link to the original text 】
- One 、numpy Installation
- Two 、Numpy Medium matrix array Basic properties of
- 3、 ... and 、 Create a matrix
- Four 、 Print matrix
- 5、 ... and 、 Basic operation
- 6、 ... and 、 The generic function
- 7、 ... and 、 Indexes 、 Slicing and iteration
- 8、 ... and 、 The matrix shape The operation of
- Nine 、 Stacking between different matrices
- Ten 、 adopt newaxis Add a dimension to the existing matrix
- 11、 ... and 、 Cut the matrix into many smaller matrices
- Twelve 、 Copy and view
- 13、 ... and 、 Advanced use of indexes
- fourteen 、 Generate a Cartesian product from two arrays
One 、numpy Installation
If you use the system directly python Environmental Science , Then use the following command to install
pip install numpy
If you use pipenv Virtual environment created by tools , Then use the following command :
pipenv install numpy
Two 、Numpy Medium matrix array Basic properties of
ndim: dimension
such as 3x4 Matrix , its ndim by 2shape: A few lines and columns , Represented by tuples
such as 3x4 matrix , its shape by (3,4)size: The total number of elements
such as 3x4 Matrix , its size by 12dtype: Type of element
You can use it directly python Type in ,numpy Some types such as numpy.int32, numpy.int16, numpy.float64 etc.itemsize: The size of the element
Memory occupied by each element , Unit is byte , For example, when type int64, be itemsize by 8 Bytes , Equivalent to dtype.itemsize
Examples are as follows , among arr=np.arange(12).reshape((3,4)) Is used to create a 3x4 Matrix , The element is 0-11, How to create a matrix will be explained in detail later , This is to demonstrate the properties of a matrix
>>> import numpy as np
>>> arr=np.arange(12).reshape((3,4))
>>> arr
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> arr.ndim
2
>>> arr.shape
(3, 4)
>>> arr.dtype
dtype('int32')
>>> arr.dtype.name
'int32'
>>> arr.size
12
>>> arr.itemsize
4
>>> type(arr)
<class 'numpy.ndarray'>
>>>
3、 ... and 、 Create a matrix
3.1 By using Python Of list perhaps tuple To create a matrix
as follows , Use one-dimensional lists respectively , One dimensional tuples , 2 d list , A two-dimensional tuple creates a matrix
>>> import numpy as np
>>> arr=np.array([1,2,3])
>>> arr
array([1, 2, 3])
>>> arr=np.array((1,2,3))
>>> arr
array([1, 2, 3])
>>> arr=np.array([[1,2,3],[4,5,6]])
>>> arr
array([[1, 2, 3],
[4, 5, 6]])
>>> arr=np.array(((1,2,3),(4,5,6)))
>>> arr
array([[1, 2, 3],
[4, 5, 6]])
>>>
There's a little bit of caution here ,np.array The argument to is a list or element , It is not possible to give several elements directly , Here is a common mistake for beginners
>>> import numpy as np
>>> arr=np.array(1,2,3,4)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: array() takes from 1 to 2 positional arguments but 4 were given
The correct should be as follows :
>>> import numpy as np
>>> arr=np.array([1,2,3,4])
>>> arr
array([1, 2, 3, 4])
In addition, when creating a matrix , You can also specify the type of data , Let's take a look at the case when the data type is not specified , Default data type , Of course, this is related to the computer platform , as follows , By default 32 Bit int type
>>> import numpy as np
>>> arr=np.array([1,2,3])
>>> arr
array([1, 2, 3])
>>> arr.dtype
dtype('int32')
>>>
as follows , You can pass dtype Parameter specifies the type of matrix element
>>> import numpy as np
>>> arr=np.array([1,2,3],dtype=np.int64)
>>> arr
array([1, 2, 3], dtype=int64)
>>> arr.dtype
dtype('int64')
>>>
3.2 Create a matrix through common basic functions
The common functions are as follows
- zeros: Create all elements as 0 Matrix
- ones: Create all elements as 1 Matrix
- empty: Create a matrix with random elements , By default empty The element type created by the function is float64, Of course, you can also pass dtype Parameter specified type .
- arange: Be similar to python in range Function of , You can generate a sequence of equal differences by specifying the initial and end values and the step size , Yes, of course reshape Function to convert the generated one-dimensional arithmetic sequence into a multi-dimensional matrix .
- linspace: By specifying the start and end values and the number of generated numbers , And then it automatically performs equal difference segmentation , It can also be done by reshape Function to convert the generated one-dimensional list into a multi-dimensional matrix
Examples are as follows :
>>> import numpy as np
>>> arr=np.zeros((3,4))
>>> arr
array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
>>> arr=np.ones((3,4))
>>> arr
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
>>> arr=np.empty((3,4))
>>> arr
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
>>> arr=np.empty((3,4),dtype=np.int32) >>> arr array([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]]) >>> arr=np.arange(0,12,1).reshape((3,4))
>>> arr
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> arr=np.arange(0,24,2).reshape((3,4))
>>> arr
array([[ 0, 2, 4, 6],
[ 8, 10, 12, 14],
[16, 18, 20, 22]])
>>> arr=np.linspace(1,100,12).reshape((3,4))
>>> arr
array([[ 1., 10., 19., 28.],
[ 37., 46., 55., 64.],
[ 73., 82., 91., 100.]])
>>>
Four 、 Print matrix
numpy When printing multidimensional matrix , The following layout will be followed
- The last dimension prints from left to right
- The penultimate dimension prints from top to bottom
- The rest are printed from top to bottom , And each dimension is separated by an empty line
The following is a table by table print 、 A two-dimensional 、 The three dimensional matrix
>>> import numpy as np
>>> arr=np.arange(6)
>>> print(arr)
[0 1 2 3 4 5]
>>> b=np.arange(12).reshape((3,4))
>>> print(b)
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
>>> c=np.arange(24).reshape((2,3,4))
>>> print(c)
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]
>>>
If there are too many matrix elements , be numpy There will be only a corner , The middle one uses … Instead of , as follows :
>>> import numpy as np
>>> arr=np.arange(10000)
>>> print(arr)
[ 0 1 2 ... 9997 9998 9999]
>>> arr=np.arange(10000).reshape((100,100))
>>> print(arr)
[[ 0 1 2 ... 97 98 99]
[ 100 101 102 ... 197 198 199]
[ 200 201 202 ... 297 298 299]
...
[9700 9701 9702 ... 9797 9798 9799]
[9800 9801 9802 ... 9897 9898 9899]
[9900 9901 9902 ... 9997 9998 9999]]
>>>
Of course, if you want to print all the elements, you can also set , By using set_printoptions To control
np.set_printoptions(threshold=sys.maxsize)
5、 ... and 、 Basic operation
The basic addition, subtraction, multiplication, division and power is the addition, subtraction, multiplication, division and power between the elements of a matrix , as follows
>>> import numpy as np
>>> a=np.array([1,2,3,4])
>>> b=np.arange(4)
>>> a
array([1, 2, 3, 4])
>>> b
array([0, 1, 2, 3])
>>> a+b
array([1, 3, 5, 7])
>>> a-b
array([1, 1, 1, 1])
>>> a*b
array([ 0, 2, 6, 12])
>>> b/a
array([0. , 0.5 , 0.66666667, 0.75 ])
>>> a>0
array([ True, True, True, True])
>>> a**2
array([ 1, 4, 9, 16])
>>> b>2
array([False, False, False, True])
>>> np.sin(a)
array([ 0.84147098, 0.90929743, 0.14112001, -0.7568025 ])
>>> np.cos(a)
array([ 0.54030231, -0.41614684, -0.9899925 , -0.65364362])
>>> np.tan(a)
array([ 1.55740772, -2.18503986, -0.14254654, 1.15782128])
Dot multiplication of matrices uses dot Or use @ Symbol , as follows :
>>> a=np.array([[1,1],[0,1]])
>>> b=np.array([[2,0],[3,4]])
>>> a
array([[1, 1],
[0, 1]])
>>> b
array([[2, 0],
[3, 4]])
>>> a*b
array([[2, 0],
[0, 4]])
>>> [email protected]
array([[5, 4],
[3, 4]])
>>> a.dot(b)
array([[5, 4],
[3, 4]])
>>> np.dot(a,b)
array([[5, 4],
[3, 4]])
>>>
Some operators, such as += or *=, It will directly process the existing matrix instead of creating a new matrix , as follows , among np.random.default_rng(1) Is the default random number generator
>>> import numpy as np
>>> rng=np.random.default_rng(1)
>>> a=np.ones((2,3),dtype=np.int32) >>> b=rng.random((2,3))
>>> a
array([[1, 1, 1],
[1, 1, 1]])
>>> b
array([[0.51182162, 0.9504637 , 0.14415961],
[0.94864945, 0.31183145, 0.42332645]])
>>> a*=3
>>> a
array([[3, 3, 3],
[3, 3, 3]])
>>> b+=a
>>> b
array([[3.51182162, 3.9504637 , 3.14415961],
[3.94864945, 3.31183145, 3.42332645]])
>>> a+=b
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
numpy.core._exceptions._UFuncOutputCastingError: Cannot cast ufunc 'add' output from dtype('float64') to dtype('int32') with casting rule 'same_kind'
>>>
When multiple types are involved in the operation , The result will follow the principle of upward conversion , as follows :
>>> import numpy as np
>>> a=np.ones(3,dtype=np.int32)
>>> b=np.linspace(0,np.pi,3)
>>> a
array([1, 1, 1])
>>> b
array([0. , 1.57079633, 3.14159265])
>>> c=a+b
>>> c
array([1. , 2.57079633, 4.14159265])
>>> b.dtype
dtype('float64')
>>> c.dtype
dtype('float64')
>>> d=np.exp(c*1j)
>>> d
array([ 0.54030231+0.84147098j, -0.84147098+0.54030231j,
-0.54030231-0.84147098j])
>>> d.dtype
dtype('complex128')
>>>
Calculate the sum of all the elements of the matrix 、 Maximum 、 Minimum function , namely sum、max and min, as follows :
>>> import numpy as np
>>> a=np.arange(12).reshape((3,4))
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> a.sum()
66
>>> np.sum(a)
66
>>> a.max()
11
>>> np.max(a)
11
>>> a.min()
0
>>> np.min(a)
0
>>>
adopt axis Parameters can evaluate elements and by row or column 、 Maximum and minimum , When axis=0 when , Means by column , When axis=1 when , By line , as follows
>>> import numpy as np
>>> a=np.arange(12).reshape((3,4))
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> a.sum(axis=0)
array([12, 15, 18, 21])
>>> np.sum(a,axis=0)
array([12, 15, 18, 21])
>>> a.sum(axis=1)
array([ 6, 22, 38])
>>> np.sum(a,axis=1)
array([ 6, 22, 38])
>>> a.max(axis=0)
array([ 8, 9, 10, 11])
>>> np.max(a,axis=0)
array([ 8, 9, 10, 11])
>>> a.max(axis=1)
array([ 3, 7, 11])
>>> np.max(a,axis=1)
array([ 3, 7, 11])
>>> a.min(axis=0)
array([0, 1, 2, 3])
>>> np.min(a,axis=0)
array([0, 1, 2, 3])
>>> a.min(axis=1)
array([0, 4, 8])
>>> np.min(a,axis=1)
array([0, 4, 8])
>>>
6、 ... and 、 The generic function
The common functions are as follows :
- sin
- cos
- exp
- sqrt
- add
- all
- any
- apply_along_axis
- argmax
- argmin
- argsort
- average
- bincount
- ceil
- clip
- conj
- corrcoef
- cov
- cross
- cumprod
- cumsum
- diff
- dot
- floor
- inner
- invert
- lexsort
- max
- maximum
- mean
- median
- min
- minimum
- nonzero
- outer
- prod
- re
- round
- sort
- std
- sum
- trace
- transpose
- var
- vdot
- vectorize
- where
Examples are as follows :
>>> import numpy as np
>>> a=np.arange(3)
>>> a
array([0, 1, 2])
>>> np.exp(a)
array([1. , 2.71828183, 7.3890561 ])
>>> np.sqrt(a)
array([0. , 1. , 1.41421356])
>>> b=np.array([4,5,6])
>>> b
array([4, 5, 6])
>>> np.add(a,b)
array([4, 6, 8])
>>>
7、 ... and 、 Indexes 、 Slicing and iteration
7.1 Index of one-dimensional matrix 、 Slicing and iteration are used
Index of one-dimensional matrix 、 Slicing and iteration use methods like python Index of the list in 、 section 、 Same as iteration , as follows :
>>> import numpy as np
>>> a=np.arange(10)
>>> a
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> a[2]
2
>>> a[2:5]
array([2, 3, 4])
>>> a[:6:2]
array([0, 2, 4])
>>> a[::-1]
array([9, 8, 7, 6, 5, 4, 3, 2, 1, 0])
>>> for i in a:
... print(i)
...
0
1
2
3
4
5
6
7
8
9
>>>
7.2 Index of multidimensional matrix 、 Slicing and iteration
Index of multidimensional matrix 、 Slicing and iteration , The main difference is that each dimension uses an index , The middle is separated by commas , as follows :
>>> import numpy as np
>>> a=np.arange(20).reshape((5,4))
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]])
>>> a[2,3]
11
>>> a[0:4,1]
array([ 1, 5, 9, 13])
>>> a[:,1]
array([ 1, 5, 9, 13, 17])
>>> a[1:3:,:]
array([[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> for elem in a[:,1]:
... print(elem)
...
1
5
9
13
17
>>> for elem in a[:,:]:
... print(elem)
...
[0 1 2 3]
[4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]
[16 17 18 19]
>>>
When the number of indexes provided is less than the dimension of the matrix , The following defaults to :, as follows a[2], It's the equivalent of a[2,:]
>>> import numpy as np
>>> a=np.arange(20).reshape((4,5))
>>> a
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]])
>>> a[2]
array([10, 11, 12, 13, 14])
>>>
When multidimensional matrix , You can replace other dimensions by using three points , For example, the following assumptions a Is a five dimensional matrix , be :
- a[1,2,…] Equivalent to a[1,2,:,:,:]
- a[…,3] Equivalent to a[:,:,:,:,3]
- a[4,…,5,:] Equivalent to a[4,:,:,5,:]
as follows
>>> import numpy as np
>>> a=np.arange(24).reshape((2,3,4))
>>> a
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
>>> a[1,...]
array([[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]])
>>> a[1,:,:]
array([[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]])
>>> a[...,2]
array([[ 2, 6, 10],
[14, 18, 22]])
>>> a[:,:,2]
array([[ 2, 6, 10],
[14, 18, 22]])
>>>
When a multidimensional matrix is traversed, it is usually traversed according to the first dimension , When you want to traverse each element , have access to flat attribute , as follows
>>> import numpy as np
>>> a=np.arange(12).reshape((3,4))
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> for elem in a:
... print(elem)
...
[0 1 2 3]
[4 5 6 7]
[ 8 9 10 11]
>>> for elem in a.flat:
... print(elem)
...
0
1
2
3
4
5
6
7
8
9
10
11
>>>
8、 ... and 、 The matrix shape The operation of
For a matrix, the following three methods do not change the matrix shape Original value
- ravel: Expand the matrix into a one-dimensional matrix
- T: Matrix rank transformation
- reshape: To readjust shape, But it will not modify the original shape
as follows
>>> import numpy as np
>>> a=np.arange(12).reshape((3,4))
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b=a.ravel()
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
>>> c=a.reshape(6,2)
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> c
array([[ 0, 1],
[ 2, 3],
[ 4, 5],
[ 6, 7],
[ 8, 9],
[10, 11]])
>>> d=a.T
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> d
array([[ 0, 4, 8],
[ 1, 5, 9],
[ 2, 6, 10],
[ 3, 7, 11]])
>>> a.shape
(3, 4)
>>> a.T.shape
(4, 3)
>>> e=a.reshape((6,2))
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> e
array([[ 0, 1],
[ 2, 3],
[ 4, 5],
[ 6, 7],
[ 8, 9],
[10, 11]])
>>>
If you want to change the shape Adjustment , have access to resize function , as follows , You can find resize Function is to adjust the original matrix directly , And there's no return value , That is, in the following example b It's empty
>>> import numpy as np
>>> a=np.arange(12).reshape((3,4))
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b=a.resize(6,2)
>>> a
array([[ 0, 1],
[ 2, 3],
[ 4, 5],
[ 6, 7],
[ 8, 9],
[10, 11]])
>>> b
>>>
Reuse reshape Function , If a dimension is set to -1, Indicates that this dimension is automatically calculated , as follows
>>> import numpy as np
>>> a=np.arange(12).reshape((3,4))
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b=a.reshape(6,-1)
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b
array([[ 0, 1],
[ 2, 3],
[ 4, 5],
[ 6, 7],
[ 8, 9],
[10, 11]])
>>>
Nine 、 Stacking between different matrices
Horizontal and vertical stacking between different matrices , as follows
>>> import numpy as np
>>> a=np.arange(4).reshape((2,2))
>>> b=np.arange(4,8).reshape((2,2))
>>> a
array([[0, 1],
[2, 3]])
>>> b
array([[4, 5],
[6, 7]])
>>> np.vstack((a,b))
array([[0, 1],
[2, 3],
[4, 5],
[6, 7]])
>>> np.hstack((a,b))
array([[0, 1, 4, 5],
[2, 3, 6, 7]])
>>>
column_stack Only in two-dimensional matrix is it equivalent to hstack, and row_stack Namely vstack Another name for , as follows
>>> import numpy as np
>>> a=np.arange(3)
>>> b=np.arange(3,6)
>>> a
array([0, 1, 2])
>>> b
array([3, 4, 5])
>>> np.column_stack((a,b))
array([[0, 3],
[1, 4],
[2, 5]])
>>> np.hstack((a,b))
array([0, 1, 2, 3, 4, 5])
>>> np.row_stack((a,b))
array([[0, 1, 2],
[3, 4, 5]])
>>> np.vstack((a,b))
array([[0, 1, 2],
[3, 4, 5]])
>>> a=np.arange(4).reshape((2,2))
>>> b=np.arange(4,8).reshape((2,2))
>>> a
array([[0, 1],
[2, 3]])
>>> b
array([[4, 5],
[6, 7]])
>>> np.column_stack((a,b))
array([[0, 1, 4, 5],
[2, 3, 6, 7]])
>>> np.hstack((a,b))
array([[0, 1, 4, 5],
[2, 3, 6, 7]])
>>> np.row_stack((a,b))
array([[0, 1],
[2, 3],
[4, 5],
[6, 7]])
>>> np.vstack((a,b))
array([[0, 1],
[2, 3],
[4, 5],
[6, 7]])
>>> np.column_stack is np.hstack
False
>>> np.row_stack is np.vstack
True
>>>
Ten 、 adopt newaxis Add a dimension to the existing matrix
To put it simply, I will newaxis Where is the parameter placed , The dimension corresponding to the location is set to 1, Examples are as follows
>>> import numpy as np
>>> a=np.array([1,2,3,4])
>>> a
array([1, 2, 3, 4])
>>> a.shape
(4,)
>>> b=a[:,np.newaxis]
>>> b
array([[1],
[2],
[3],
[4]])
>>> b.shape
(4, 1)
>>> c=a[np.newaxis,:]
>>> c
array([[1, 2, 3, 4]])
>>> c.shape
(1, 4)
>>>
11、 ... and 、 Cut the matrix into many smaller matrices
The partition matrix can use hsplit and vsplit, The parameter can be a number , Indicates that the matrix is divided into columns or rows n A small matrix , It can also be an element , It means to split after the column or row corresponding to each number in the tuple , as follows
>>> import numpy as np
>>> a=np.arange(24).reshape((4,6))
>>> a
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]])
>>> np.hsplit(a,3) # It means that you will a Divided into... By column 3 A small matrix
[array([[ 0, 1],
[ 6, 7],
[12, 13],
[18, 19]]), array([[ 2, 3],
[ 8, 9],
[14, 15],
[20, 21]]), array([[ 4, 5],
[10, 11],
[16, 17],
[22, 23]])]
>>> np.vsplit(a,2) # It means that you will a Divided into... By line 2 A small matrix
[array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]]), array([[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]])]
>>> np.hsplit(a,(2,4)) # It means that you will a As listed in 2 Column and the first 4 Split after column
[array([[ 0, 1],
[ 6, 7],
[12, 13],
[18, 19]]), array([[ 2, 3],
[ 8, 9],
[14, 15],
[20, 21]]), array([[ 4, 5],
[10, 11],
[16, 17],
[22, 23]])]
>>> np.vsplit(a,(1,3)) # It means that you will a Divide by line after the first and third lines
[array([[0, 1, 2, 3, 4, 5]]), array([[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17]]), array([[18, 19, 20, 21, 22, 23]])]
>>>
Twelve 、 Copy and view
12.1 No copy occurs
When directly assigning values or passing objects in functions , There will be no copying , The function passes arguments because in python What is passed in is a reference to an object , So there will be no copying , as follows
>>> import numpy as mp
>>> a=np.array([1,2,3,4])
>>> b=a
>>> a
array([1, 2, 3, 4])
>>> b
array([1, 2, 3, 4])
>>> b is a
True
>>> def f(x):
... print(id(x))
...
>>> id(a)
2211569938384
>>> f(a)
2211569938384
>>>
12.2 View or light copy
adopt view The view created by the function is essentially a shallow copy , The copied objects are resize Does not affect the source object , However, the operation of modifying the value will cause the corresponding value of the source matrix to be modified synchronously , In addition, slicing essentially produces a new view , as follows
>>> import numpy as np
>>> a=np.arange(12).reshape((3,4))
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b=a.view()
>>> b
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> id(a)
2211558280336
>>> id(b)
2211569938192
>>> b is a
False
>>> b.base is a
False
>>> b.flags.owndata
False
>>> b.resize((2,6))
>>> b
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b[0,0]=100
>>> b
array([[100, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])
>>> a
array([[100, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> c=a[:,0:2]
>>> c
array([[100, 1],
[ 4, 5],
[ 8, 9]])
>>> c.flags.owndata
False
>>> c[0,0]=10000
>>> c
array([[10000, 1],
[ 4, 5],
[ 8, 9]])
>>> a
array([[10000, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b
array([[10000, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11]])
>>>
12.3 Deep copy
adopt copy The object created by the function is a deep copy , That is, modifying the value of the newly generated object will not affect the source matrix , as follows
>>> import numpy as np
>>> a=np.arange(12).reshape((3,4))
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b=a.copy()
>>> b
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b.base is a
False
>>> b[0,0]=100
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b
array([[100, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>>
13、 ... and 、 Advanced use of indexes
An index can also be a list , In this way, multiple data can be fetched at one time , as follows
>>> import numpy as np
>>> arr=np.arange(10,20)
>>> arr
array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19])
>>> index=np.array([1,1,3,7,4])
>>> index
array([1, 1, 3, 7, 4])
>>> arr[index]
array([11, 11, 13, 17, 14])
>>> index=np.array([[1,2,3],[4,5,6],[3,4,7]])
>>> index
array([[1, 2, 3],
[4, 5, 6],
[3, 4, 7]])
>>> arr[index]
array([[11, 12, 13],
[14, 15, 16],
[13, 14, 17]])
>>>
When the matrix is two-dimensional data , The elements in the indexed matrix represent each row , Such as the following
>>> import numpy as np
>>> arr=np.arange(10,22).reshape((3,4))
>>> arr
array([[10, 11, 12, 13],
[14, 15, 16, 17],
[18, 19, 20, 21]])
>>> index=np.array([0,1,0,2])
>>> arr[index]
array([[10, 11, 12, 13],
[14, 15, 16, 17],
[10, 11, 12, 13],
[18, 19, 20, 21]])
>>> index=np.array([[0,1,1,0],[1,2,2,1]])
>>> index
array([[0, 1, 1, 0],
[1, 2, 2, 1]])
>>> arr[index]
array([[[10, 11, 12, 13],
[14, 15, 16, 17],
[14, 15, 16, 17],
[10, 11, 12, 13]],
[[14, 15, 16, 17],
[18, 19, 20, 21],
[18, 19, 20, 21],
[14, 15, 16, 17]]])
>>>
Besides , When the source matrix is multidimensional , You can get a number at a specified position by using two index matrices when indexing , At this point, the two index matrices need to have the same shape, as follows
>>> import numpy as np
>>> arr=np.arange(10,22).reshape((3,4))
>>> arr
array([[10, 11, 12, 13],
[14, 15, 16, 17],
[18, 19, 20, 21]])
>>> i=np.array([[0,1],[1,2]])
>>> j=np.array([[2,1],[3,3]])
>>> i
array([[0, 1],
[1, 2]])
>>> j
array([[2, 1],
[3, 3]])
>>> arr[i,j]
array([[12, 15],
[17, 21]])
>>> arr[i,2]
array([[12, 16],
[16, 20]])
>>> arr[:,j]
array([[[12, 11],
[13, 13]],
[[16, 15],
[17, 17]],
[[20, 19],
[21, 21]]])
>>>
A Boolean matrix can be used to assign values to a matrix , as follows
>>> import numpy as np
>>> a=np.arange(12).reshape((3,4))
>>> a
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> b=a>4
>>> b
array([[False, False, False, False],
[False, True, True, True],
[ True, True, True, True]])
>>> a[b]
array([ 5, 6, 7, 8, 9, 10, 11])
>>> a[b]=0
>>> a
array([[0, 1, 2, 3],
[4, 0, 0, 0],
[0, 0, 0, 0]])
>>>
fourteen 、 Generate a Cartesian product from two arrays
Use np.ix_() The mapping relationship of Cartesian product can be generated according to the input two arrays , as follows , among np.ix_([0,1,2,3],[0,1,2]) Will produce (0,0),(0,1),(0,2),(1,0,(1,1,(1,2),(2,0),(2,1),(2,2), Then index the matrix , Therefore, the expected results are as follows
>>> import numpy as np
>>> index=np.ix_([0,1,2,3],[0,1,2])
>>> index
(array([[0],
[1],
[2],
[3]]), array([[0, 1, 2]]))
>>> arr=np.arange(24).reshape((4,6))
>>> arr[index]
array([[ 0, 1, 2],
[ 6, 7, 8],
[12, 13, 14],
[18, 19, 20]])
>>> arr
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]])
>>>
边栏推荐
- R language plot visualization: plot visualizes the normalized histogram, adds the density curve KDE to the histogram, and uses geom at the bottom edge of the histogram_ Adding edge whisker graph with
- SAP OData 开发教程 - 从入门到提高(包含 SEGW, RAP 和 CDP)
- 8 自定义评估函数
- STEPN 新手入门及进阶
- JS教程之使用 ElectronJS、VueJS、SQLite 和 Sequelize ORM 从 A 到 Z 创建多对多 CRUD 应用程序
- How to separate jar packages and resource files according to packaging?
- How to implement interface current limiting?
- [Blue Bridge Cup training 100 questions] scratch distinguishing prime numbers and composite numbers Blue Bridge Cup scratch competition special prediction programming question intensive training simul
- Redis的ACID
- R语言使用cor函数计算相关性矩阵进行相关性分析,使用corrgram包可视化相关性矩阵、行和列使用主成分分析重新排序、下三角形中使用平滑的拟合线和置信椭圆,上三角形中使用散点图、对角线最小值和最大值
猜你喜欢

Solana capacity expansion mechanism analysis (1): an extreme attempt to sacrifice availability for efficiency | catchervc research

SAP OData development tutorial - from getting started to improving (including segw, rap and CDP)

100+数据科学面试问题和答案总结 - 基础知识和数据分析

Svg savage animation code

2 三种建模方式
Practice of federal learning in Tencent micro vision advertising

10 tf. data

【力扣刷题】单调栈:84. 柱状图中最大的矩形
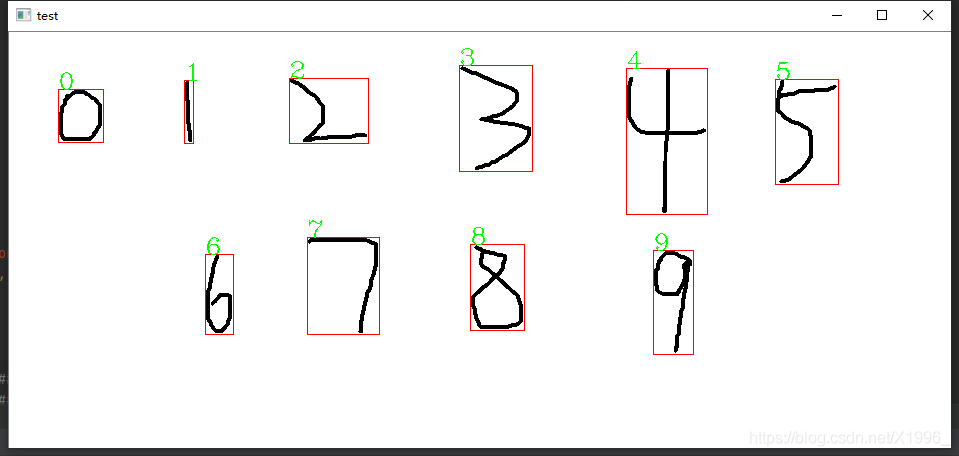
Handwritten numeral recognition, run your own picture with the saved model

How to implement interface current limiting?
随机推荐
11 introduction to CNN
Development, deployment and online process of NFT project (2)
油田勘探问题
How to separate jar packages and resource files according to packaging?
李飞飞团队将ViT用在机器人身上,规划推理最高提速512倍,还cue了何恺明的MAE...
JS教程之使用 ElectronJS 桌面应用程序打印贴纸/标签
stm32h7b0替代h750程序导致单片机挂掉无法烧录程序问题
H5 close the current page, including wechat browser (with source code)
C# 读写文件从用户态切到内核态,到底是个什么流程?
JVM notes
Net based on girdview control to delete and edit row data
Stepn novice introduction and advanced
Net基于girdview控件实现删除与编辑行数据
Redis order sorting command
C. Inversion Graph
Solidus labs welcomes zhaojiali, former head of financial innovation in Hong Kong, as a strategic adviser
【蓝桥杯集训100题】scratch辨别质数合数 蓝桥杯scratch比赛专项预测编程题 集训模拟练习题第15题
Svg rising Color Bubble animation
LeetCode 单周赛298,前三题
The first batch in the industry! Tencent cloud security and privacy computing products based on angel powerfl passed CFCA evaluation
