当前位置:网站首页>The little schemer - the origin of the y-zygote cycle
The little schemer - the origin of the y-zygote cycle
2022-07-23 18:22:00 【Glucose o_ o】
What is recursion ?
(define length
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
Above is length The implementation of the function calculates the data set in the form of recursion l The length of .
without define How do we define this assignment operation length function ? In other words, how do we use anonymous functions to complete recursion .
(lambda (l)
(cond
((null? l) 0)
(else (add1 (enternity (cdr l))))))
This anonymous function determines if the length of the input parameter list is 0 Then return to 0, If the length of the input parameter list exceeds 0 No result will be returned , So this anonymous function can only calculate length 0 The length value of the list of , You can name it for convenience length0.
notes :enternity Is an infinite recursive function , There will be no result back . See supplement for implementation 1.
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length0 (cdr l))))))
Because I can't use length0 The name , So let's talk about length0 Replace with the corresponding anonymous function :
(lambda (l)
(cond
((null? l) 0)
(else
(add1
((lambda (l)
(cond
((null ? l) 0)
(else (add1
(enternity (cdr l))))))
(cdr l))))))
This anonymous function can be called length≤1, Because it can only judge that the length is less than or equal to 1 list .
According to this rule, it can also be written length≤2:
(lambda (l)
(cond
((null? l) 0)
(else
(add1
((lambda (l)
(cond
((null ? l) 0)
(else (add1
((lambda (l)
(cond
(null ? l) 0)
(else (add1 (enternity (cdr l)))))
(cdr l))))))
(cdr l))))))
Such code can be written all the time , But there is no guarantee that the written function will be enough .
Through observation, we can find that the function of each anonymous function is to enter the parameter list and output the length of the parameter list , So you can give anonymous functions a name length. take length0 Make some changes :
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))
enternity)
Right again length≤1 Make some changes
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))
enternity))
Through this method, you can also length≤2 Make changes
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))
enternity)))
By introducing length After the parameter transformation, the function can still see obvious repetition .
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))
This part of the function input, which has been repeated many times, is a length function , The function realized is to produce a length function , So it can be named mk-length.
(lambda (mk-length)
(mk-length enternity)
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))))
The above is revised length0 function
length≤1:
(lambda (mk-length)
(mk-length
(mk-length enternity))
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))))
length≤2:
(lambda (mk-length)
(mk-length
(mk-length
(mk-length enternity)))
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))))
To increase the length of the function processing list here, you only need to increase one level mk-length Function call , But it still hasn't been solved. Facing the list of unknown length, the function always ends its call .
Let's analyze it briefly length≤2 The implementation steps of :
The first step is to execute the innermost (mk-length enternity) obtain length0,length0 Namely mk-length Anonymous function returned by function , Only in the context of this anonymous function length yes enterity.
The second is the implementation of the middle tier (mk-length length0) obtain length≤1,length≤1 yes mk-length Anonymous function returned by function , Only in the context of this anonymous function length yes length0.
Finally, the outermost level is executed mk-length length≤1 obtain length≤2,length≤2 yes mk-length Anonymous function returned by function , Only in the context of this anonymous function length yes length≤1.
PS:mk-length The function returned is length function , That's what I mentioned above length0、length≤1 and length≤2 etc. .
That's it length≤2 The function is finished . Next, I'll give you a brief introduction length≤2 Use list (a b c) The execution process as an input .
First execute the function length≤2,(a b c) The list is not empty , take (length≤1 (b c)) Return the result plus 1 return .
Second, execute the function length≤1,(b c) The list is not empty , take (length0 ) Return the result plus 1 return .
Execute the function again length0,(c) The list is not empty , take (enterity ()) Return the result plus 1 return .
because enterity Infinite loop cannot exit, resulting in this length≤2 Function into the reference (a b c) No results .
This is a right to left installation , The process performed from left to right .length≤1 In equal function length Is the function passed in from the previous step , But the previous step here refers to the previous step of the installation process , Not the last step in the implementation process .
By facing up to length≤2 The analysis of the function execution process finds that when it is executed to enternity The whole process was interrupted . How to make length Keep it going ? To execute length You need to mk-length, however mk-length At present, you cannot quote yourself . What do I do ?
(lambda (mk-length)
(mk-length enternity)
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))))
Because of the function enternity Infinite recursion does not return , So will enternity Replace with mk-length It seems to have no effect on the result .
(lambda (mk-length)
(mk-length mk-length)
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))))
as long as mk-length The unification of names in functions will not affect the operation of functions , So you can length Replace with the name mk-length.
(lambda (mk-length)
(mk-length mk-length)
(lambda (mk-length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (mk-length (cdr l))))))))
That's it mk-length Cannot quote your own problem , Next, we need to solve the problem of not being able to cycle indefinitely .
Now it will length Renamed as mk-length, that mk-length It's production length Of , In need of use length Where can be used mk-length To generate a length.
(lambda (mk-length)
(mk-length mk-length)
(lambda (mk-length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 ((mk-length enterity) (cdr l))))))))
Use (apples) Disassemble the execution steps of the above function as parameters .
First step , take mk-length Execute as input (mk-length mk-length)
((lambda (mk-length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 ((mk-length enterity) (cdr l)))))))
(lambda (mk-length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 ((mk-length enterity) (cdr l))))))))
The second step , Put the second mk-length Pass in the first as an input mk-length
(lambda (l)
(cond
((null? l) 0)
(else (add1 (
(lambda (mk-length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 ((mk-length enterity) (cdr l)))))))
enterity) (cdr l)))))
The third step , take enterity As mk-length Pass in lambda (mk-length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (
(lambda (l)
(cond
((null? l) 0)
(else (add1 ((enterity enterity) (cdr l)))))))
(cdr l)))))
Step four , Will list (apples) Bring in the above function to get the result 1
If the incoming is
(apples bananas), Execution will be interrupted at (enterity enterity)
Look at the function just obtained
(lambda (mk-length)
(mk-length mk-length)
(lambda (mk-length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 ((mk-length enterity) (cdr l))))))))
Make some changes
((lambda (mk-length)
(mk-length mk-length))
(lambda (mk-length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 ((mk-length mk-length) (cdr l))))))))
This will reveal , Whenever it's going to dry up (mk-length mk-length) accounting Calculate a new function For use . Yes (mk-length mk-length) The return value of looks like a length function .
So far, the recursive implementation of anonymous functions has been completed length The needs of , But we still need to simplify it and conclude a general pattern , Implementing any anonymous function can fulfill the requirement of recursion .
take (mk-length mk-length) Extracted as length Pass in :
(lambda (mk-length)
(mk-length mk-length)
(lambda (mk-length)
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
(mk-length mk-length)))
Disassemble the above function and you will get
((lambda (mk-length)
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
(mk-length mk-length))
(lambda (mk-length)
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
(mk-length mk-length)))
((lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
((lambda (mk-length)
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
(mk-length mk-length))
(lambda (mk-length)
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
(mk-length mk-length))))
((lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
((lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))
((lambda (mk-length)
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
(mk-length mk-length))
(lambda (mk-length)
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
(mk-length mk-length))))))
There's no end to this , take mk-length Pass to mk-length And immediately execute (mk-length mk-length) Will continue to get (mk-length mk-length), Need to continue (mk-length mk-length), This has never stopped .
We need to go back to the original right way .
((lambda (mk-length)
(mk-length mk-length))
(lambda (mk-length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 ((mk-length mk-length) (cdr l))))))))
The extraction in the above way will lead to infinite recursion because (mk-length mk-length) The call of will immediately get a (mk-length mk-length) This will continue to recurse infinitely .
It's out (mk-length mk-length) In this way, the extraction method of immediate call can also delay the call , (lambda (l) ((mk-length mk-length) l)) This will only call length When it is called (mk-length mk-length)
((lambda (mk-length)
(mk-length mk-length))
(lambda (mk-length)
((lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l)))))))
(lambda (l) ((mk-length mk-length) l)))))
So far, we have basically completed the anonymous function length Recursive simplification , The last step is to extract it .
((lambda (le)
((lambda (mk-length)
(mk-length mk-length))
(lambda (mk-length)
(le (lambda (l)
((mk-length mk-length) l))))))
(lambda (length)
(lambda (l)
(cond
((null? l) 0)
(else (add1 (length (cdr l))))))))
Look at the general pattern
(lambda (le)
((lambda (mk-length)
(mk-length mk-length))
(lambda (mk-length)
(le (lambda (l)
((mk-length mk-length) l))))))
This pattern is named Y Combiner
(define Y
(lambda (le)
((lambda (f) (f f))
(lambda (f)
(le (lambda (x) ((f f) x)))))))
That's all Y The context of the combo .
Add 1:
(define enternity
(lambda (l)
(enternity l)))
边栏推荐
- Tencent tore open the "fig leaf" of China's NFT
- "Nowadays, more than 99.9% of the code is garbage!"
- @Entity 里面的 JPA 注解
- SQLZOO——BBC QUIZ
- 【Coggle 30 Days of ML】糖尿病遗传风险检测挑战赛(2)
- How the lock issued by go works (combined with the source code)
- 物联网之Zigbee系统开发一(zigbee简介)[通俗易懂]
- MySQL 66 questions, 20000 words + 50 pictures, including (answer analysis)
- MySQL8.0.23四次重装都失败在 'Writing configuration file'
- 错误“ Failed to fetch “xxx”Temporary failure resolvingW: Some index files failed to download“解决办法
猜你喜欢

Salary high voltage line

20220721 积分环节的时频域分析

Three barriers in the workplace: annual salary of 300000, 500000 and 1million

Seata
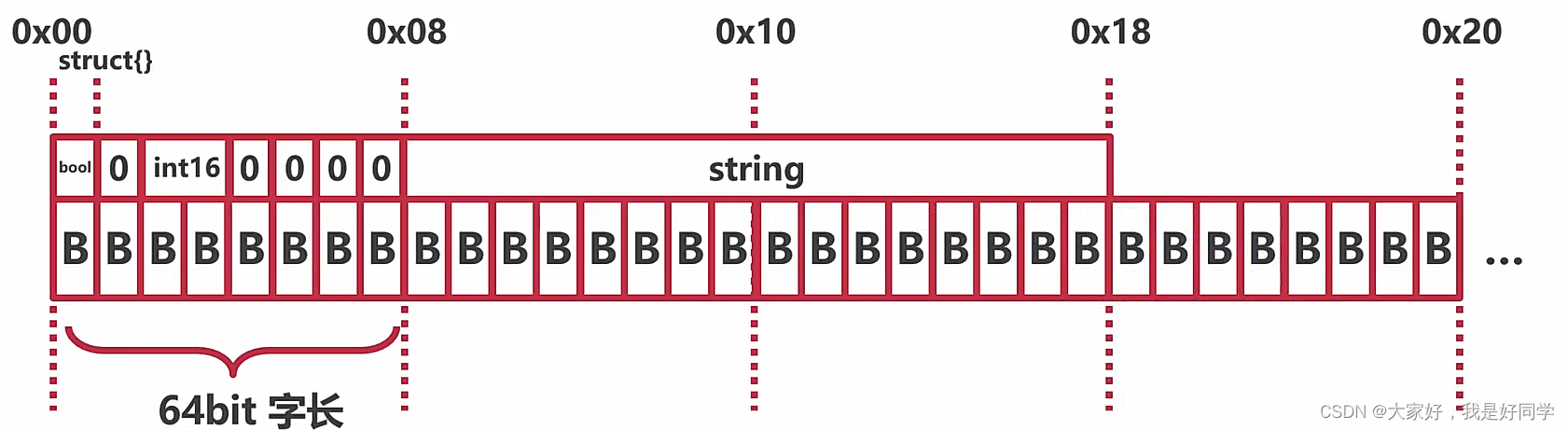
go语言中的内存对齐是如何优化程序效率的?

How to evaluate the accuracy of stock analysts' prediction?

What happened behind kubectl's creation of pod?

Data concentration analysis and data distribution

serialization and deserialization
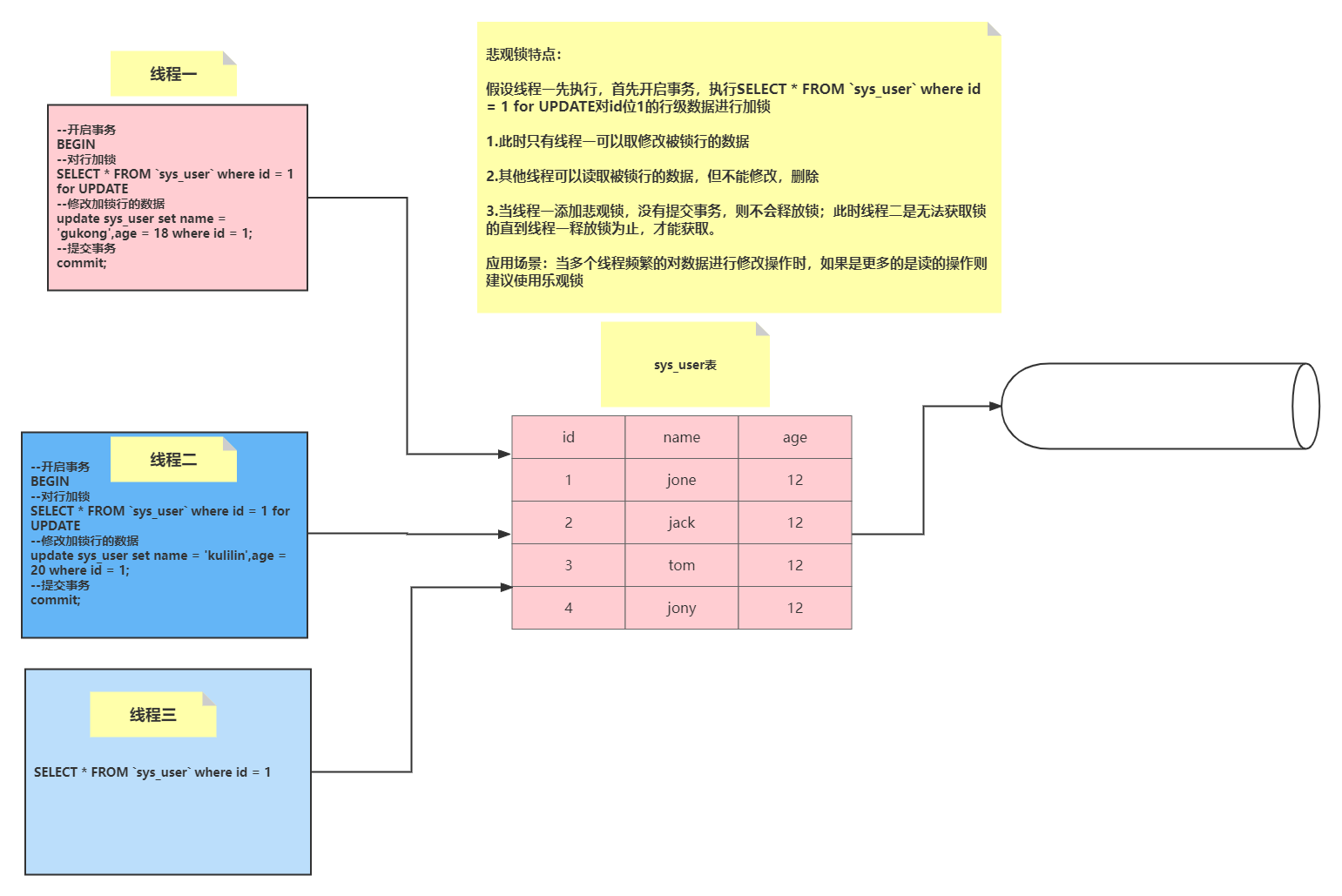
Pessimistic lock and optimistic lock
随机推荐
rhcsa笔记五
MySQL 7 kinds of join (Figure)
Do you still have certificates to participate in the open source community?
变分法 (Calculus of Variations)
【通俗易懂】关系模式范式分解教程 3NF与BCNF口诀!小白也能看懂「建议收藏」
JS 将伪数组转换成数组
MySQL 8.0.23 failed to reinstall for four times in'writing configuration file'
CSDN custom T-shirts are waiting for you to get, and the benefits of new programmer are coming!
WARNING: Your password has expired. Password change required but no TTY available.
Machine learning (9) - Feature Engineering (3) (supplementary)
"Nowadays, more than 99.9% of the code is garbage!"
Type-C to OTG (USB2.0 data transmission) + PD charging protocol chip ledrui ldr6028/ldr6023ss
Sentinel installation diagram
Flame Graphs 火焰图安装与使用
[easy to understand] relational schema paradigm decomposition tutorial 3NF and BCNF formula! Xiaobai can also understand "suggestions collection"
Prevent and control the summer market blowout after adjustment, and evaluate the summer activities of Tujia, muniao and meituan
前置放大器和功率放大器有什么区别?
SQLZOO——BBC QUIZ
从业务开发中学习和理解架构设计
知乎二面:请问Redis 如何实现库存扣减操作和防止被超卖?