当前位置:网站首页>221. 最大正方形
221. 最大正方形
2022-07-31 01:20:00 【ZNineSun】
打卡!!!每日一题
今天继续给大家分享一道动态规划类型的题目,不过该题目的状态转移方程比较难以理解,我会详细的给大家分析一下
题目描述:
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积。
题目示例:

本题思路很简单,直接暴力解决,两个for循环遍历,一直遍历到最右下的结点,然后找到一个面积最大值,由于时间复杂度太高,也对不起我们的智商(PS:听我吹吹牛就算了,在真正笔试或者面试的时候一定要用最快的速度解决出来,只要能AC就是厉害),下面我们讨论一下动态规划的解决办法。
我们定义dp[i][j],表示以(i,j)为右下角的,且只包含 1 的正方形的边长最大值
通俗来讲,就像上图所示红色区域下对应的正方形,当然这个正方形可能没那么大,我只是随便画了一个供大家理解一下右下角的含义。
如果我们能计算出所有 dp(i,j) 的值,那么其中的最大值即为矩阵中只包含 1 的正方形的边长最大值,其平方即为最大正方形的面积。
那么如何计算 dp 中的每个元素值呢?对于每个位置 (i, j),检查在矩阵中该位置的值:
- 如果该位置的值是 0,则 dp(i, j) = 0,因为当前位置不可能在由 1 组成的正方形中;
- 如果该位置的值是 1,则 dp(i,j) 的值由其上方、左方和左上方的三个相邻位置的 dp 值决定。具体而言,当前位置的元素值等于三个相邻位置的元素中的最小值加 1,状态转移方程如下:
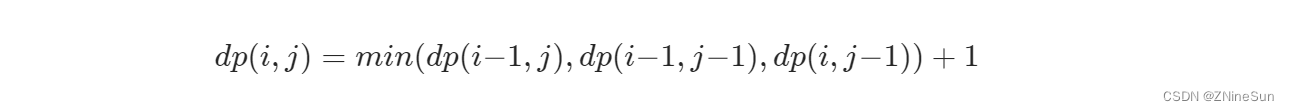
我帮大家理解一下为啥取这三个里面的最小值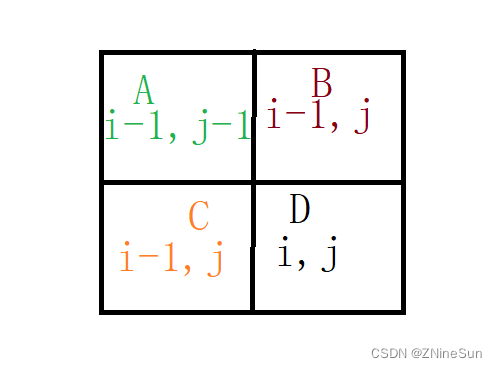
我们假设A,B,C的形状如下: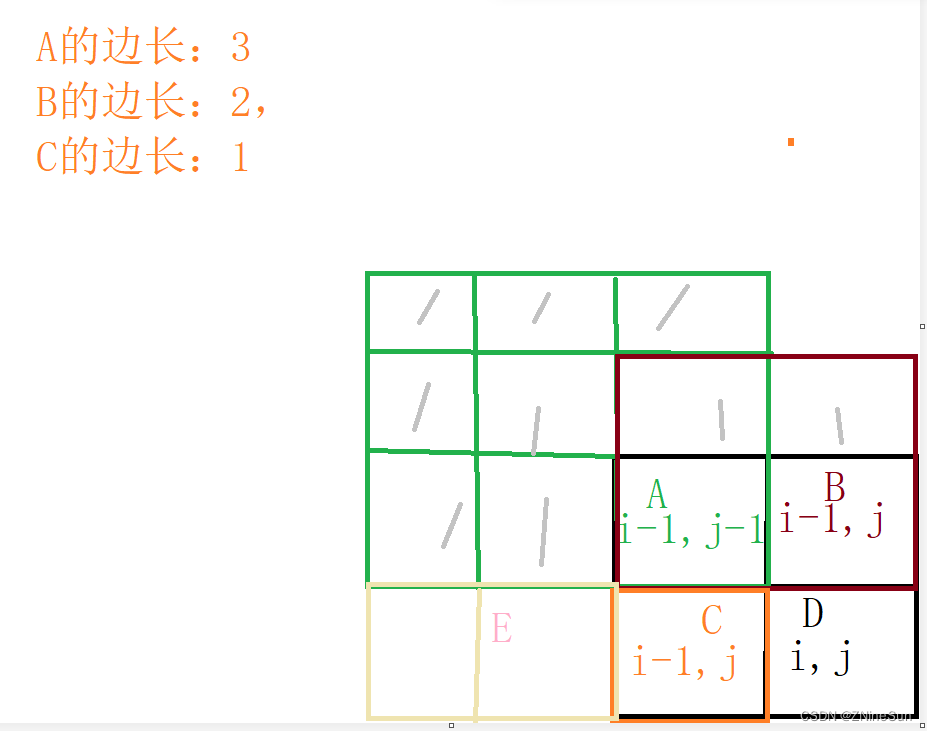
说明E区域里面的值一定是0,否则的话C的边长就可以取2了
如果D的边长取A的边长+1,即D的边长=4,那么其组成的大正方形,一定包含E区域,这就不合理了,因为题目要求的是我们的正方形必须全部为1
如果还是不理解,下面留言吧,实在不行,我有空录制个视频来给大家讲解一下。
如果这个理解了,代码就很简单了:
public int maximalSquare(char[][] matrix) {
int row = matrix.length;
int coloumn = matrix[0].length;
if (row <= 1 && coloumn <= 1) {
return matrix[0][0];
}
int[][] dp = new int[row][coloumn];
for (int r = 0; r < row; r++) {
for (int c = 0; c < coloumn; c++) {
if (matrix[r][c] == '0') {
dp[r][c] = 0;
} else {
if (r - 1 < 0 || c - 1 < 0) {
dp[r][c] = 1;
} else {
dp[r][c] = Math.min(Math.min(dp[r][c - 1], dp[r - 1][c]), dp[r - 1][c - 1]) + 1;
}
}
}
}
int max = dp[0][0];
for (int i = 0; i < row; i++) {
for (int j = 0; j < coloumn; j++) {
max = Math.max(dp[i][j], max);
}
}
return max * max;
}
边栏推荐
猜你喜欢

孩子的编程启蒙好伙伴,自己动手打造小世界,长毛象教育AI百变编程积木套件上手

Centos 7.9安装PostgreSQL14.4步骤

Centos 7.9 install PostgreSQL14.4 steps
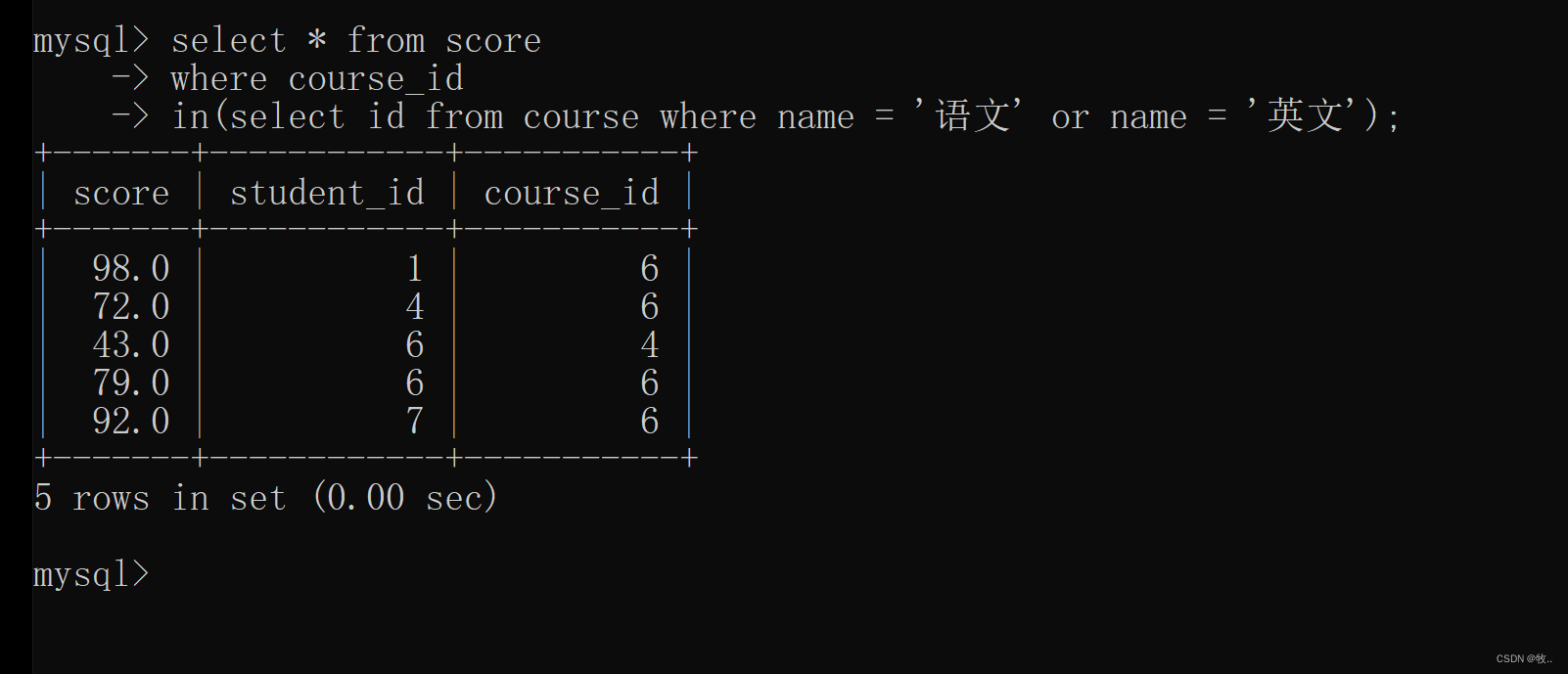
MySQL (6)

typescript17 - function optional parameters
I have been working in software testing for 3 years, how did I go from just getting started to automated testing?
Chi-square distribution of digital image steganography
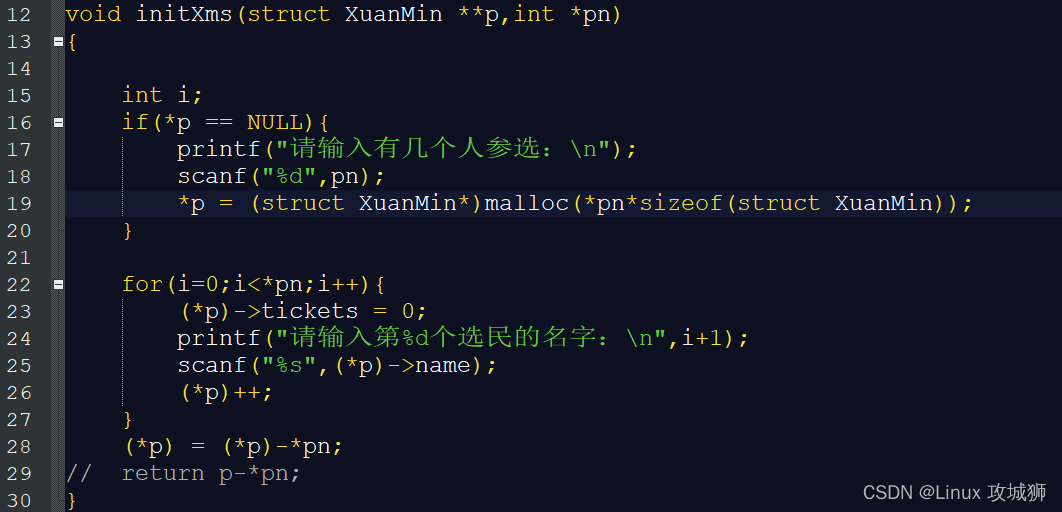
C language _ structure pointer array function voting system

RTL8720DN开发笔记一 环境搭建与mqtt实例

typescript9 - common base types
随机推荐
Solution: Parameter 0 of method ribbonServerList in com.alibaba.cloud.nacos.ribbon.NacosRibbonClientConfigu
API 网关 APISIX 在Google Cloud T2A 和 T2D 的性能测试
小黑leetcode之旅:117. 填充每个节点的下一个右侧节点指针 II
BOM系列之Navigator对象
RTL8720DN开发笔记一 环境搭建与mqtt实例
C语言_结构体指针数组函数选票系统
typescript13-类型别名
4G通信模块CAT1和CAT4的区别
Centos 7.9安装PostgreSQL14.4步骤
【网络安全】文件上传靶场通关(1-11关)
Distributed. Idempotency
.NET 跨平台应用开发动手教程 |用 Uno Platform 构建一个 Kanban-style Todo App
typescript10-commonly used basic types
Rocky/GNU之Zabbix部署(2)
Multiplication, DFS order
PDF 拆分/合并
tkinter模块高级操作(二)—— 界面切换效果、立体阴影字效果及gif动图的实现
DOM系列之 offset 系列
【952. Calculate the maximum component size according to the common factor】
查看zabbix-release-5.0-1.el8.noarch.rpm包内容