152. Product maximum subarray

Clock in !!! A daily topic

Today, I will continue to share with you Dynamic programming Type of topic .

Title Description ：

Give you an array of integers nums , Please find the non empty continuous subarray with the largest product in the array （ The subarray contains at least one number ）, And returns the product of the subarray .

The answer to the test case is 32- position Integers .

Subarray Is a continuous subsequence of an array .

Title Example ：

At first, I saw this problem , Very contemptuous of it , Thinking this is a very basic dynamic planning problem , As usual , Find the state transition equation .

namely dp[i]： To i The product of the largest continuous subarray corresponding to nodes .
Then there are dp[i]=max{nums[i],nums[i]*dp[i-1]}

Take the topic as an example 1 For example ：
Initial value ：dp[0]=nums[0]=2;
dp[1]=max{nums[1],nums[1]*dp[0]}=6
dp[2]=max{nums[2],nums[2]*dp[1]}=-2
dp[3]=max{nums[3],nums[3]*dp[2]}=4

So I quickly wrote the following code ：

    public int maxProduct(int[] nums) {
    
        int length = nums.length;
        if (length <= 1) {
    
            return nums[0];
        }
        int[] dp = new int[length];
        dp[0] = nums[0];
        for (int i = 1; i < length; i++) {
    
            dp[i] = Math.max(nums[i], dp[i - 1] * nums[i]);
        }
        // Search for maximum 
        int max = dp[0];
        for (int i = 1; i < length; i++) {
    
            max = Math.max(max, dp[i]);
        }
        return max;
    }

But when I submit test cases , Find out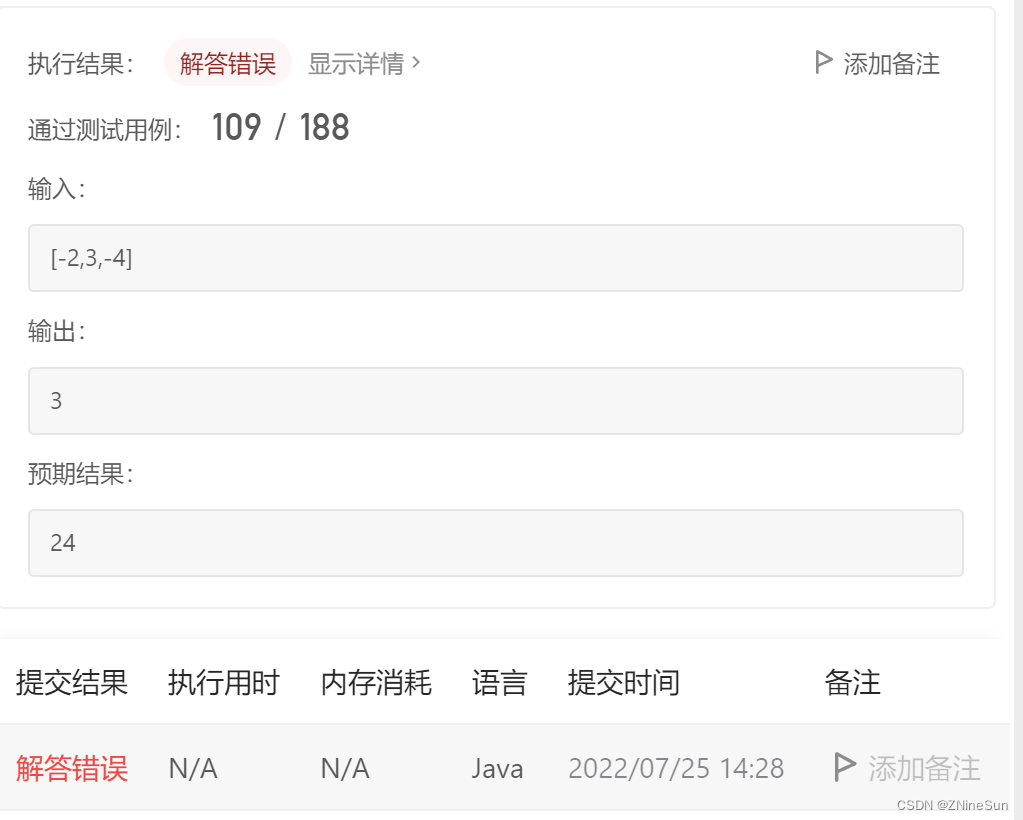

Then I realized that I had neglected one situation , Because according to my idea above
dp[0]=nums[0]=-2;
dp[1]=max{nums[1],nums[1]*dp[0]}=3
dp[2]=max{nums[2],nums[2]*dp[1]}=-4
Finally, the maximum value of Tao 3

In the above process , I ignored the negative value , That is to say, the front may be negative , Then multiply by a negative value , It will become a larger value .

The solution is simple ： We just need the original dp On the basis of , Then compare a minimum value with nums[i] Multiply by , Then we have to introduce one dp_min To store the minimum , So there is ：

• dp_max[i]: Storage and nums[i] Multiply Maximum Values of contiguous subarrays
• dp_min[i]: Storage and nums[i] Multiply Minimum Values of contiguous subarrays

The corresponding state transition equation is as follows ：

• dp_max[i]=max{nums[i],dp_max[i - 1] * nums[i], dp_min[i - 1] * nums[i])}
• dp_min[i]=min{nums[i],dp_max[i - 1] * nums[i], dp_min[i - 1] * nums[i]}

Initial value ：

• dp_max[0]=nums[0]
• dp_min[0]=nums[0]

The corresponding code is as follows ：

    public int maxProduct(int[] nums) {
    
        int length = nums.length;
        if (length <= 1) {
    
            return nums[0];
        }
        int[] dp_max = new int[length];// Storage maximum 
        int[] dp_min = new int[length];// Storage minimum 
        dp_max[0] = nums[0];
        dp_min[0] = nums[0];
        for (int i = 1; i < length; i++) {
    
            dp_max[i] = Math.max(nums[i], Math.max(dp_max[i - 1] * nums[i], dp_min[i - 1] * nums[i]));
            dp_min[i] = Math.min(nums[i], Math.min(dp_max[i - 1] * nums[i], dp_min[i - 1] * nums[i]));
        }
        int ans = dp_max[0];
        for (int i = 1; i < length; i++) {
    
            ans = Math.max(ans, dp_max[i]);
        }
        return ans;
    }