当前位置:网站首页>Mathematical modeling - linear programming
Mathematical modeling - linear programming
2022-06-25 17:16:00 【Herding cattle】
Catalog
Basic concepts
An important branch of operations research is mathematical programming , Linear programming is an important branch of mathematical programming .
Variables are called The decision variables , The goal of the plan is called Objective function , The restriction is called constraint condition ,s.t. yes “ Bound ” It means .
The general steps of establishing a linear programming model are :① To analyze problems , Find out the decision variables .② Find equality or inequality constraints .③ Construct a linear function about decision variables .
General form of linear programming model :

or :
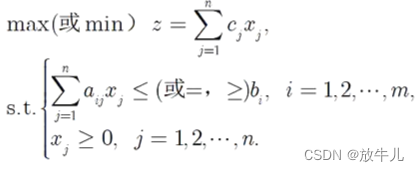

![c=[c_{1},c_{2},...,c_{n}]^{T}](http://img.inotgo.com/imagesLocal/202206/25/202206251650024986_1.gif) Is the coefficient vector of the objective function , Also called value vector ;
Is the coefficient vector of the objective function , Also called value vector ;![x=[x_{1},x_{2},...,x_{n}]^{T}](http://img.inotgo.com/imagesLocal/202206/25/202206251650024784_12.gif) Is the decision vector ;
Is the decision vector ; Is the coefficient matrix of the constrained equations ;
Is the coefficient matrix of the constrained equations ;![b=[b_{1},b_{2},...,b_{m}]^{T}](http://img.inotgo.com/imagesLocal/202206/25/202206251650024986_9.gif) Is the constant vector of the constrained equations .
Is the constant vector of the constrained equations .
And standard :

The objective function is very large , The constraints are equality constraints . The solution satisfying the constraint conditions is a feasible solution , Making the objective function reach the maximum value is called the optimal solution . The set of all feasible solutions is called feasible region , Write it down as R.
In the process of solving mathematical programming problems , Be sure to calculate Sensitivity analysis . Sensitivity analysis refers to the analysis of the sensitivity of the system due to changes in surrounding conditions . For linear programming problems a、b、c Are set to constant , But in practice , These coefficients will change a little .
Model solving and application
MATLAB There are two models for solving mathematical programming problems in : Solver based solution method and Problem based solution ,
Solver based solution method
It is necessary to convert linear programming into standard form :

The objective function must be minimized , Constraints are divided into less than or equal to constraints and equal sign constraints ,lb and ub Is the upper and lower bounds of decision variables .
MATLAB The function call format is :
[x,fval] = linprog(f,A,b)
[x,fval] = linprog(f,A,b,Aeq,beq)
[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub)
x Returns the value of the decision variable ,fval It returns the optimal value of the objective function ,f It's the value vector ,A,b Corresponding to the linear inequality constraint ,Aeq and beq Corresponding to the constraints of linear equality ,lb and ub Corresponding to the lower bound vector and the upper bound vector of the decision vector respectively .
This method can only be applied to The decision vector is one-dimensional The situation of .
Problem based solution
First, the optimization problem is constructed with variables and expressions , And then use solve Function solving , It can be used doc optimproblem view help .
①prob=optimproblem('ObjectiveSense','max');
ObjectiveSense It can be max and min, Represents the maximum or minimum value of optimization , The default is min
② Definition f,A,b( ditto ,f Can be defined as a row vector , In this way, the objective function is different and then transposed )
③x=optimvar('x',2,1,'TYPE','integer','LowerBound',0,'UpperBound',inf);
first ‘x’ Inside is the variable name , Column vector , Then there are several rows and columns .
‘TYPE’, What is defined later is the type of the function , for instance integer Integer type ,double Double precision models
‘LowerBound' And 'UpperBound' Indicates what the lower and upper bounds follow 0,inf They are the scope
④prob.Objective=f * x;% Objective function , The objective function needs to get a scalar value , Not a matrix vector
⑤prob.Constraints.con=A*x<=b;% constraint condition , There is only one constraint , Or you can skip it .con,.con Is the label , You can name it yourself , When there are multiple constraints , Must label cannot be the same .
⑥[sol fval flag out]=solve(prob);%fval It's the best value ,sol.x Is the value of the decision variable , When there are multiple decision variables , Sure sol.y,flag Don't worry about in linear programming , Note that it cannot be negative in nonlinear programming .
for example :
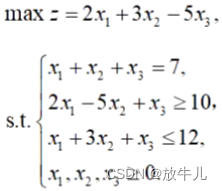
Use solver to solve :
clc,clear
f = [-2;-3;5];% To find the minimum
A = [-2,5,-1;1,3,1];
b = [-10;12];
Aeq = [1,1,1];
beq = [7];
lb = zeros(3,1);
[x,fval] = linprog(f,A,b,Aeq,beq,lb,[]);
x
-fvalx =
6.4286
0.5714
0
ans =14.5714
Use problem-based solutions
clc,clear
prob=optimproblem('ObjectiveSense','max');
x=optimvar('x',3,'LowerBound',0);
prob.Objective=2*x(1) + 3*x(2) - 5*x(3);
prob.Constraints.con1=2*x(1) - 5*x(2) + x(3)>=10;
prob.Constraints.con2=x(1) + 3*x(2) + x(3)<=12;
prob.Constraints.con3=x(1) + x(2) + x(3)==7;
[sol fval flag out]=solve(prob);
sol.x
fvalans =
6.4286
0.5714
0
fval =14.5714
other
- MATLAB in , Load existing txt Matrix of documents , If use load function , Then the number of rows and columns of the matrix should be equal . If individual numbers are missing , You can use readmatrix function .writematrix(a,'data.xlsx') Can write Excel in .
- Matrix index a(1:end,1),end It is automatically the last column of the row
- sum(a,'all') According to matrix a The sum of all the elements of
边栏推荐
- 上线移动ERP系统有哪些步骤?环环紧扣很重要
- 从业一年,我是如何涨薪13K+?
- LSF如何看job预留slot是否合理?
- et al和etc区别
- Comprehensive optimization of the six topics, Alibaba performance optimization booklet open source, leading you to the ultimate performance
- Sword finger offer II 025 Adding two numbers in a linked list
- 微信公众号服务器配置
- 【编译原理】词法分析
- 学习太极创客 — MQTT(一)MQTT 是什么
- 剑指 Offer 50. 第一个只出现一次的字符
猜你喜欢

微信公众号服务器配置

Kotlin
Uncover ges super large scale graph computing engine hyg: Graph Segmentation

XXIX - orbslam2 real-time 3D reconstruction using realsensed435

二十九-使用RealSenseD435进行ORBSLAM2实时三维重建

Solution to the problem of incorrect clock in FreeRTOS kernel

万卷书 - 大力娃的书单

上线移动ERP系统有哪些步骤?环环紧扣很重要

Batch --07--- breakpoint lifting

学习太极创客 — MQTT(三)连接MQTT服务端
随机推荐
宝藏又小众的国画3d材质贴图素材网站分享
Problems encountered in using MySQL
Protocol and hierarchy
pytorch官方文档学习记录
mood
【Matlab】曲线拟合
这些老系统代码,是猪写的么?
SnakeYAML配置文件解析器
ES6知识点
Involution? Foam? Change? Ten questions directly hit the core puzzle of "meta universe" – the essence of "ask ta- Wang Lei about the time of the universe"
Differences between et al and etc
软考中级和高级选哪个比较好?
Sword finger offer 50 First character that appears only once
Wireshark network card cannot be found or does not display the problem
万卷书 - 大力娃的书单
MySQL 用 limit 为什么会影响性能?
社交电商如何运营推广?
【无标题】
Vscode plug-in self use
How do components communicate