zk-SNARK： About private key 、 Ring signature 、ZKKSP

Private key

Theoretically , A zero knowledge proof can be constructed for any mathematical problem (ZKP), Without having to disclose its solution . In practice , Develop for a problem ZKP It is usually necessary to invent a new cryptographic algorithm . It has no standard “ formula ”, What is needed is extensive and in-depth knowledge of cryptography . for example ,ZK The puzzle of involves ∑-protocol and ZK key-statement proof Pedersen Commitment and Fiat-Shamir heuristic .

zk-SNARK For any problem ZKP Generate and standardize . Just use ZK The format expresses the original problem to be proved , For example, using a specific language Circom or Zokrates. The rest are made up of generic zk-SNARK Frame handling , It hides all the complexity of the underlying cryptography .

stay zk-SNARK Before , Build for new problems ZKP It is similar to designing new ZKP When building new applications ASIC.zk-SNARK It allows you to use the general “ZK CPU” Program to build new ZKP. The former needs a Cryptologist , The latter only needs a programmer , Greatly reduced ZKP Entry threshold .

To demonstrate the power of this paradigm shift , We use it to build one of the most popular ZKP： Given public key ( That is, discrete logarithm ) Private key knowledge .

Private key knowledge ZKP

To lock bitcoin to the public key / Address , The owner must show that he knows the corresponding private key . But he can't be public , Otherwise bitcoin may be stolen . This is done by digital signature , It is ZKP² A form of . We will show how to use zk-SNARK Another way to achieve the same goal .

In bitcoin , Public key Q It's the private key d Multiply by the generator G.

Below Circom The code realizes the bitcoin elliptic curve secp256k1 Scalar multiplication over . We can easily use it to prove Q yes d The public key ：

• Will be the first 3 The input scalar of the row is set to d： Be careful , It's private , Therefore, it still needs to be kept confidential .
• Will be the first 4 The input point of the line is set to G.
• Will be the first 6 The output of the row is set to Q.

// encoded with k registers of n bits each
template Secp256k1ScalarMult(n, k) {
    signal private input scalar[k];
    signal public input point[2][k];

    signal output out[2][k];

    component n2b[k];
    for (var i = 0; i < k; i++) {
        n2b[i] = Num2Bits(n);
        n2b[i].in <== scalar[i];
    }

    // has_prev_non_zero[n * i + j] == 1 if there is a nonzero bit in location [i][j] or higher order bit
    component has_prev_non_zero[k * n];
    for (var i = k - 1; i >= 0; i--) {
        for (var j = n - 1; j >= 0; j--) {
            has_prev_non_zero[n * i + j] = OR();
            if (i == k - 1 && j == n - 1) {
                has_prev_non_zero[n * i + j].a <== 0;
                has_prev_non_zero[n * i + j].b <== n2b[i].out[j];
            } else {
                has_prev_non_zero[n * i + j].a <== has_prev_non_zero[n * i + j + 1].out;
                has_prev_non_zero[n * i + j].b <== n2b[i].out[j];
            }
        }
    }

    signal partial[n * k][2][k];
    signal intermed[n * k - 1][2][k];
    component adders[n * k - 1];
    component doublers[n * k - 1];
    for (var i = k - 1; i >= 0; i--) {
        for (var j = n - 1; j >= 0; j--) {
            if (i == k - 1 && j == n - 1) {
                for (var idx = 0; idx < k; idx++) {
                    partial[n * i + j][0][idx] <== point[0][idx];
                    partial[n * i + j][1][idx] <== point[1][idx];
                }
            }
            if (i < k - 1 || j < n - 1) {
                adders[n * i + j] = Secp256k1AddUnequal(n, k);
                doublers[n * i + j] = Secp256k1Double(n, k);
                for (var idx = 0; idx < k; idx++) {
                    doublers[n * i + j].in[0][idx] <== partial[n * i + j + 1][0][idx];
                    doublers[n * i + j].in[1][idx] <== partial[n * i + j + 1][1][idx];
                }
                for (var idx = 0; idx < k; idx++) {
                    adders[n * i + j].a[0][idx] <== doublers[n * i + j].out[0][idx];
                    adders[n * i + j].a[1][idx] <== doublers[n * i + j].out[1][idx];
                    adders[n * i + j].b[0][idx] <== point[0][idx];
                    adders[n * i + j].b[1][idx] <== point[1][idx];
                }
                // partial[n * i + j]
                // = has_prev_non_zero[n * i + j + 1] * ((1 - n2b[i].out[j]) * doublers[n * i + j] + n2b[i].out[j] * adders[n * i + j])
                //   + (1 - has_prev_non_zero[n * i + j + 1]) * point
                for (var idx = 0; idx < k; idx++) {
                    intermed[n * i + j][0][idx] <== n2b[i].out[j] * (adders[n * i + j].out[0][idx] - doublers[n * i + j].out[0][idx]) + doublers[n * i + j].out[0][idx];
                    intermed[n * i + j][1][idx] <== n2b[i].out[j] * (adders[n * i + j].out[1][idx] - doublers[n * i + j].out[1][idx]) + doublers[n * i + j].out[1][idx];
                    partial[n * i + j][0][idx] <== has_prev_non_zero[n * i + j + 1].out * (intermed[n * i + j][0][idx] - point[0][idx]) + point[0][idx];
                    partial[n * i + j][1][idx] <== has_prev_non_zero[n * i + j + 1].out * (intermed[n * i + j][1][idx] - point[1][idx]) + point[1][idx];
                }
            }
        }
    }

    for (var idx = 0; idx < k; idx++) {
        out[0][idx] <== partial[0][0][idx];
        out[1][idx] <== partial[0][1][idx];
    }
}

For the sake of explanation , We use the standard double addition algorithm . The main cycle occurs in 33 Go to the first place 65 That's ok . We are the first 42 Line usage Secp256k1AddUnequal Add points ; stay 43 Line usage Secp256k1Double Double the point . In each iteration , We are all in the first 355-358 Double the line . If the current bit is set , We will also add .

Once we have Circom Code , We can use general zk-SNARK Library to prove knowledge of the private key , While maintaining its confidentiality . We have demonstrated the method without digital signature .

Proof of organization membership

below , We will show how to use zero knowledge language Circom“ Programming ” Implement another complex cryptographic primitive ： Ring signature .

Use zk-SNARK Ring signature of

In the ring signature , Group / Any member of the ring can sign to prove their membership , There is no need to disclose their specific identity . Based on signature , The verifier can determine the signature of a member of the Group , But he doesn't know which member signed it .

because zk-SNARK Programmability and composability of , We can simply “ code ” Ring signature , As shown below .

// `n`: chunk length in bits for a private key
// `k`: chunk count for a private key
// `m`: group member count
template Main(n, k, m) {
  signal private input privkey[k];
  
  signal public input pubKeyGroup[m][2][k];
  signal output existInGroup;

  // get pubkey from privkey
  component privToPub = ECDSAPrivToPub(n, k);
  for (var i = 0; i < k; i++) {
    privToPub.privkey[i] <== privkey[i];
  }

  signal pubkey[2][k];

  // assign pubkey to intermediate var
  for (var i = 0; i < k; i++) {
    pubkey[0][i] <== privToPub.pubkey[0][i];
    pubkey[1][i] <== privToPub.pubkey[1][i];
  }

  // check whether pubkey exists in group
  var exist = 0;
  component eq[2*m];
  var compareResult[m];

  for (var i = 0; i < m; i++) {
    // pubkey `x` comparer
    eq[i] = BigIsEqual(k);

    // pubkey `y` comparer
    eq[i+m] = BigIsEqual(k);

    for(var j = 0; j < k; j++) {
      // compare `x`
      eq[i].in[0][j] <== pubkey[0][j];
      eq[i].in[1][j] <== pubKeyGroup[i][0][j];

      // compare `y`
      eq[i+m].in[0][j] <== pubkey[1][j];
      eq[i+m].in[1][j] <== pubKeyGroup[i][1][j];
    }
    
    compareResult[i] = eq[i].out * eq[i+m].out;
  }

  component checker = InGroupChecker(m);
  for(var i = 0; i < m; i++) {
    checker.in[i] <== compareResult[i];
  }

  existInGroup <== checker.out;
}

From 11 Go to the first place 22 That's ok , We use the private key section ECDSAPrivToPub From 5 The private key in line derives the 16 Public key in line . then , We will get the public key and the 7 Compare each public key in the group defined in the row . If and only if it matches the 54 Any one of the lines , We go back to true.

Because the private key input is private and remains hidden , Therefore, the verifier cannot use it to identify which member created the certificate . We have created a ZKP Members of are in the Group / Ring signature of ring , Without knowing any underlying cryptography .

ZKKSP

on top , We have shown how to use what is called ZK Key-Statement proof (ZKKSP) The technique of builds a zero knowledge proof for the following statement (ZKP).

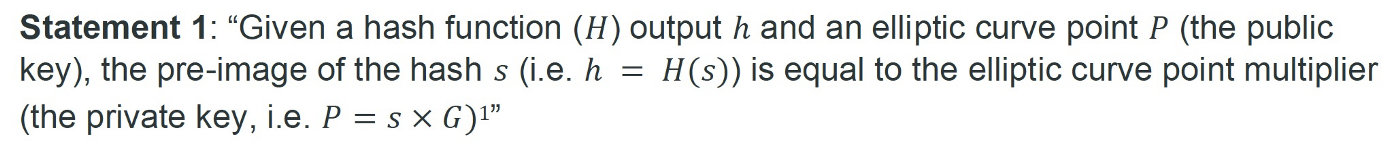
although ZKKSP work , But it has a big limitation ： It only applies to a specific form of statement , namely secret Is the private key of a given public key , And it is also the original image of a given hash . It is not clear how to extend it to a slightly modified statement , for example , In addition to the private key and the original image ,secret It is also an even number . Besides , It is proposed that it requires patent level knowledge of cryptography , Such as ∑-protocol And commitment plan .

ZKKSP Use zk-SNARK

We use zk-SNARK The programmability of ZKKSP. We will Proof of organization membership The elliptic curve point multiplication used in this part is simply combined with the hash Library . Generated Circom The code is as follows ：

// library circuits from https://github.com/0xPARC/circom-ecdsa
include "lib-circom-ecdsa/ecdsa.circom";
include "../node_modules/circomlib/circuits/sha256/sha256.circom";
include "../node_modules/circomlib/circuits/bitify.circom";

// `n`: chunk length in bits for a private key
// `k`: chunk count for a private key
template Main(n, k) {
  // n * k == 256
  assert(n * k >= 256);
  assert(n * (k-1) < 256);

  // little-endian
  signal private input privkey[k];
  signal public input pubkey[2][k];

  signal public output privkeyHash[k];

  // get pubkey from privkey
  component privToPub = ECDSAPrivToPub(n, k);
  for (var i = 0; i < k; i++) {
    privToPub.privkey[i] <== privkey[i];
  }

  // verify input pubkey
  signal pub_x_diff[k];
  signal pub_y_diff[k];
  for (var i = 0; i < k; i++) {
    pub_x_diff[i] <-- privToPub.pubkey[0][i] - pubkey[0][i];
    pub_x_diff[i] === 0;
    pub_y_diff[i] <-- privToPub.pubkey[1][i] - pubkey[1][i];
    pub_y_diff[i] === 0;
  }

  // calculate sha256 of privkey
  component sha256 = Sha256(256);
  for (var i = 0; i < k; i++) {
    for (var j =0; j < n; j++) {
      // change privkey to big-endian as sha256 input
      sha256.in[i * n + j] <-- (privkey[k-1-i] >> (n-1-j)) & 1;
    }
  }

  // set output
  component b2n[k];
  for (var i = 0; i < k; i++) {
    b2n[i] = Bits2Num(n);
    for(var j = 0; j < n; j++) {
      // `b2n` input is little-endian in bits, `sha256` out is big-endian in bits
      b2n[i].in[n-1-j] <== sha256.out[i * n + j];
    }
    privkeyHash[i] <== b2n[i].out;
  }

}

component main {public [pubkey]} = Main(64, 4);

Same as before , We are the first 15 Line usage ECDSAPrivToPub From 14 The private key of row derives a public key . Then we use No 3 Row imported sha256 In the library Sha256 Hash the same private key , To ensure that the results are consistent with 17 The given hash of the row matches . We just “ Programming ” 了 ZKKSP, There is no need to know advanced cryptography in advance . Besides , because zk-SNARK The composability of , We can easily extend it to add pairs secret Constraints .

Source：

https://xiaohuiliu.medium.com/programmable-zero-knowledge-proofs-using-zk-snarks-part-1-9599deb1db47

https://xiaohuiliu.medium.com/programmable-zero-knowledge-proofs-using-zk-snarks-part-2-890869249291

https://xiaohuiliu.medium.com/programmable-zero-knowledge-proofs-using-zk-snarks-part-3-d707dbfa2b28

About

ChinaDeFi - ChinaDeFi.com It's a research driven DeFi Innovation organizations , We are also a blockchain development team . From all over the world every day 500 Close to a good source of information 900 In the content , Looking for deeper thinking 、 Sort out more systematic content , Provide decision-making assistant materials to the Chinese market at the fastest speed .

Layer 2 friends sharing same hobby - Welcome to Layer 2 Interested blockchain technology enthusiasts 、 Study and analyze people and Gavin（ WeChat : chinadefi） contact , Discuss together Layer 2 Landing opportunities . Please pay attention to our official account of WeChat “ Decentralized financial community ”.