干货！一种被称为Deformable Butterfly（DeBut）的高度结构化且稀疏的线性变换

点击蓝字

关注我们

AI TIME欢迎每一位AI爱好者的加入！

深度神经网络在各个领域都取得了很好的效果，例如图像识别，图像切割，自动驾驶，还有坏品检测等。但是深度神经网络由于其对计算和储存资源的较高要求，使得它很难部署在在资源有限的边缘设备上。

为了解决这一问题，许多方法被用来对模型进行压缩，常见的类型有：剪枝，量化，和低秩分解。

在这项工作中，我们用不同于上述任何类别的一种新的线性变换来对模型进行了压缩，名为Deformable Butterfly (DeBut)。它是基于传统的Butterfly矩阵的一种泛化，可以适应各种输入输出维度，且继承了传统Butterfly矩阵从细粒度到粗粒度的可学习层次结构。当部署神经网络时，DeBut层的特殊结构和稀疏性构成了网络压缩的新方式。

我们将DeBut作为全连接层和卷积层的替代品来应用，并证明了它在同质化神经网络方面的优势，使其具有轻量和低复杂度等有利特性，而不致对准确率造成大幅影响。DeBut层的各种不同设计方式可以做到在复杂度和准确性之间进行基于不同考量的权衡，这为分析和实践研究开辟了新的空间。

本期AI TIME PhD直播间，我们邀请到香港大学电子电气工程学院博士生——林睿，为我们带来报告分享《一种被称为Deformable Butterfly（DeBut）的高度结构化且稀疏的线性变换》。

林睿：

香港大学(HKU)电子电气工程学院在读博士生，导师为黄毅教授，主要研究方向为神经网络的压缩和加速。个人主页：https://ruilin0212.github.io

Butterfly Matrix

我们可以把Butterfly矩阵理解为可以用一系列特殊形式的矩阵去近似任何给定的矩阵。下图左下角就是一个例子，它展示了如何用Butterfly矩阵去近似一个16*16大小的矩阵。蓝色的小方块代表非零元素，白色部分代表相应位置的元素值为0。

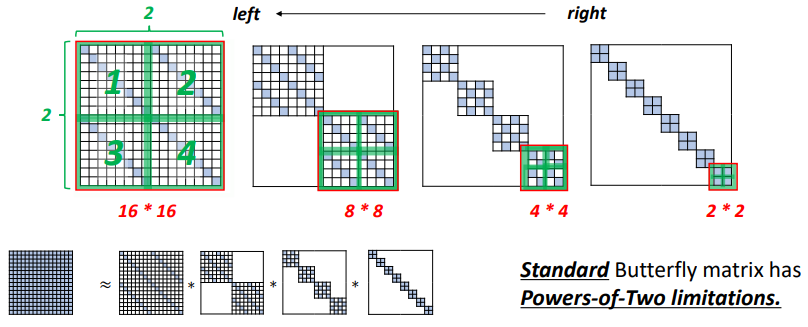
在16*16的情况中，我们可以观察到所有的Butterfly矩阵都是分块矩阵、对角矩阵。在对角线上的分块矩阵长和宽都是2的n次方。

从右到左，我们可以观察到这些分块矩阵的大小都是不断变大的，从2*2、4*4到8*8、16*16。总的来说，这是标准的Butterfly矩阵，可以被视为分块对角矩阵。并且，每个分块矩阵都是由4个对角矩阵组成的，这4个矩阵以2*2的形式排列。

因此，很明显Butterfly矩阵在形式上是有2的n次方性质的。具体来说，是它的对角矩阵必须是2的n次方。而且分块矩阵也必须是2的n次方。

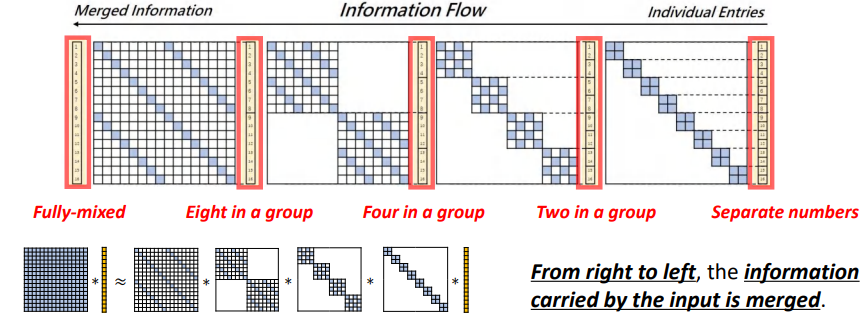
接下来，我们就从信息传递的角度来识别一下Butterfly的层次结构。

如下图左下角所示，我们使用一个向量来从给定的矩阵大小来近似一系列Butterfly因子。下图中的上半部分就展示了每一步细节：在最右的向量中数字是用来标记元素位置的，所以从上到下是1到16。

这些连接向量和Butterfly因子的虚线，标记了会被混合的向量中的元素及相应的Butterfly因子中的分块矩阵，这些分块矩阵就扮演了混合器的角色，将向量中被标记的元素所携带的信息混合到一起。

我们可以看到最右边所有的位置指标都是混合分开的，和最右边的Butterfly因子相乘之后，这些元素所带的信息被混合起来了。从2到4，最终得到16个元素混合在一起的向量，即所有元素混合在一起的向量。

Convolution as a Matrix Product

到现在，我们已经了解了标准Butterfly矩阵的性质，接下来我们要看下如何把卷积理解为矩阵的乘法。下图图A展示了我们理解的卷积操作一般形式。这里有一些3D的卷积核和一些输入，这些卷积核会沿着输入的二维平面进行滑动，然后和相应的像素进行卷积。

在进行完这些操作之后，我们就会得到一个张量输出。与之等价的通用矩阵乘法，首先会把卷积核展开。如下图中红框展示的样子，每一个卷积核都会被展开成一个矩阵。这个矩阵F行数和卷积核的数量是相等的，列数是卷积核按通道展开后向量的长度。

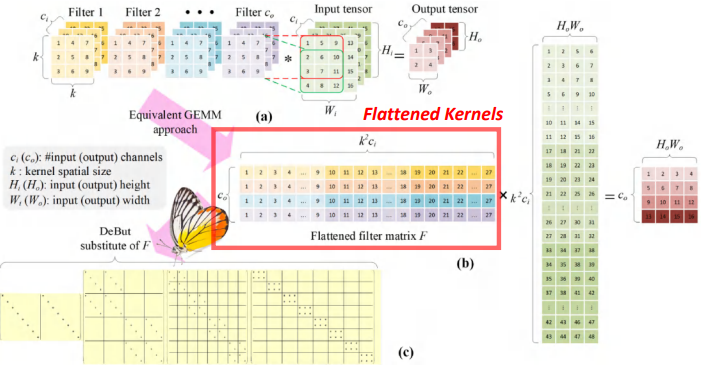
和同一个卷积核做卷积的像素会被展开成一列，同一个channel展开完是接着下一个channel展开。有许多线性变换的目标都是通过矩阵近似展开的矩阵F，于是我们思考DeBut矩阵是如何进行线性变化的呢？DeBut矩阵和标准Butterfly矩阵有什么区别呢？

DeBut Chains

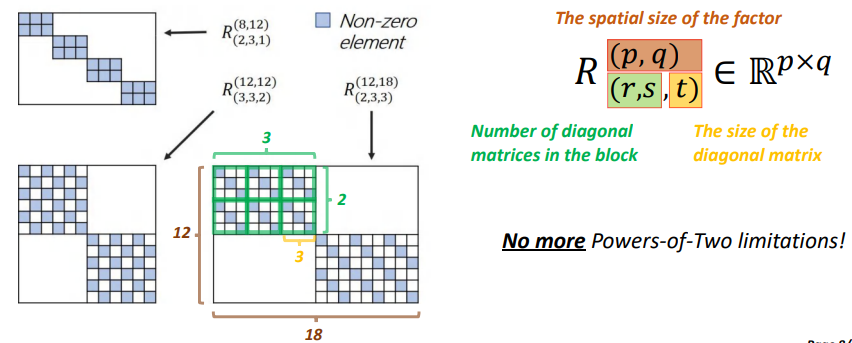
上图中的左部展示了DeBut因子的结构，右边解释了用来标记这个DeBut因子的记号是什么意思以及如何理解。

如上图右部，p，q表示的是DeBut factor的大小，r和s代表了每一个在对角线上分块矩阵的对角矩阵个数。t代表了每一个对角矩阵的大小，我们可以用左边最大的DeBut因子来诠释这个符号的意思，（p，q）为上脚标，（r，s，t）为下脚标。

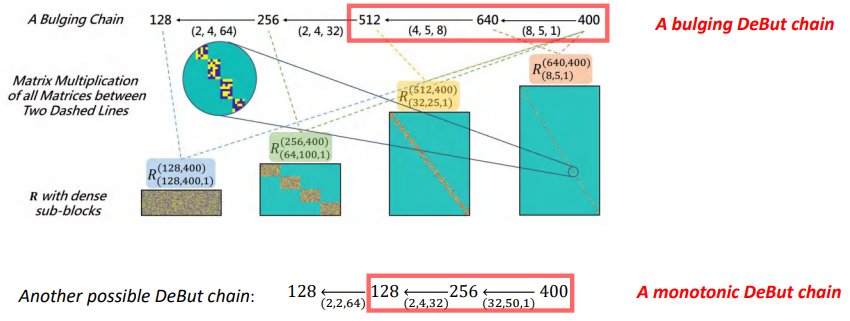
DeBut Chain可以理解为由一系列DeBut因子所组成的一个链条。我们给出两种不同的chain来近似一个大小为128*400的矩阵，分别为A bulging DeBut chain和A monotonic DeBut chain。

一般而言，我们是根据DeBut因子的大小来对DeBut Chain进行分类。如果一个DeBut Chain包含的因子行数或列数比近似的矩阵大，DeBut Chain就会被当作bulging类型的chain，否则就是monotonic类型的。具体如上图所示，这两种chain的结构可以分别用小号和单簧管来形容。

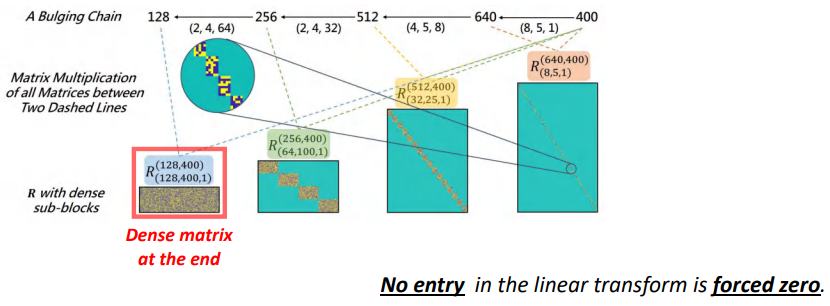
如果我们用一个合格的chain来近似一个矩阵的话，线性变换中没有矩阵元素会被长久的设置为0。如果DeBut Chain是合格的，说明没有信息会被遗漏。

如上图所示，我们把所有的DeBut因子相乘之后，上图红框内的矩阵是没有长置为0元素的，即DeBut Chain可以用来近似任何给定的矩阵。

Alternating Least Squares (ALS)

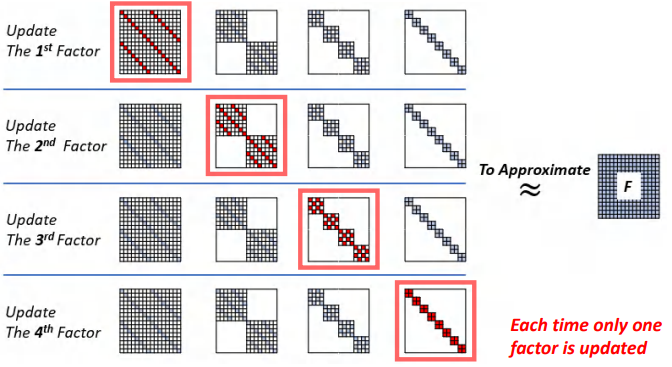
我们需要了解交替最小二乘法在DeBut Chain中初始化的应用，之前我们提到会用DeBut因子近似展开的卷积核矩阵F。对一个训练好的网络，我们可以用已知的参数对DeBut因子进行初始化。

如下图所示，我们每次只更新一条chain中的一个因子，从左到右更新所有的因子再从右到左更新一次，这个过程被称为1次横扫sweep。

我们使用如下公式来评价这个近似的性能。

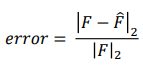
5次横扫足以对小矩阵起到很好的初始化效果。

LeNet Trained on MNIST (Baseline: 99.29%)

在实验中，我们首先选用了MNIST这个数据集，然后在简单的LeNet上做测试。我们可以看到此时的Baseline是99.29%，实际上全连接层是可以看做一个卷积层的，其核的空间大小与输入input大小是相同的。

为了快速看出DeBut有什么优势，我们挑选了LeNet中两个较大的卷积层，采用了LC和MC两个指标。结果可以看出，DeBut对每一个选定的层都有明显的提高。

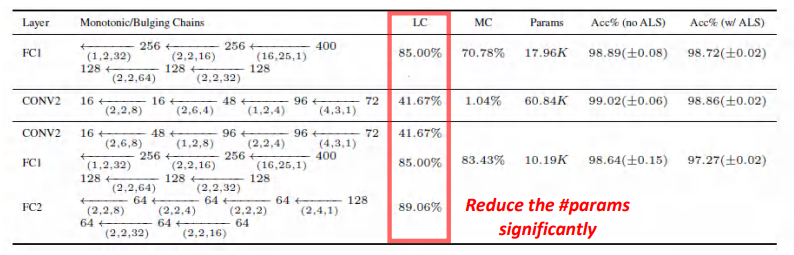
DeBut能够进一步减少参数的数量，同时提供良好的输出精度。在没有交替最小二乘的时候，模型的准确率是最好的，但是这并不能否定我们提出的ALS价值。在模型更为复杂的时候，我们的实验验证了ALS是有提升准确率效果的。

VGG Trained on CIFAR-10 (Baseline: 93.96%)

我们继续用VGG在CIFAR-10上进行训练，然后可以看到这里的baseline是93.96%。

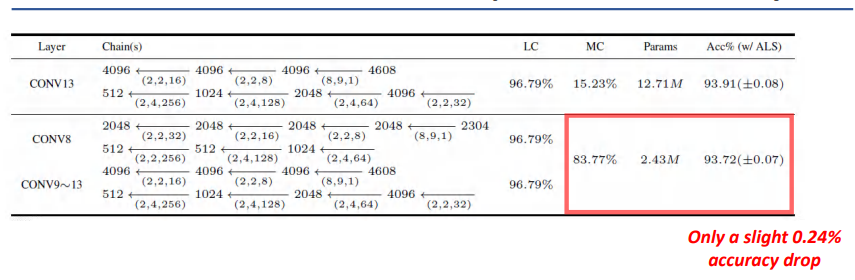
由上图，我们可以看出交替最小二乘的表现依然是比较好的。

ResNet-50 Trained on ImageNet (Baseline: 76.01%)

我们用ResNet-50在ImageNet上继续 训练，ImageNet是比之前用的数据集大得多而且更复杂的数据集。作为消融实验，我们我们分别只选用膨胀的chain或单调的chain对选中层进行替换。

对于DeBut-bulging，参数的数量减少了47.56%，准确度最高的是74.52%，较基线76.01%降低1.47%。

对于r DeBut-mono，压缩模型比DeBut-bulging少0.3M的参数，但仍然达到了74.34%的top-1精度。

DeBut vs. Other Linear Transform Schemes

最后，我们将DeBut与其他要素的方法进行了比较。在与最接近的方案进行比较之后，我们发现其是稳定的。当关注上图中最后两列时，我们发现DeBut是三种方法中最快的方法。

Adaptive Fastfood中的Fast Hadamard Transform 非常耗时，使得在大型CNN中进行多层次的Adaptive Fastfood训练非常困难。

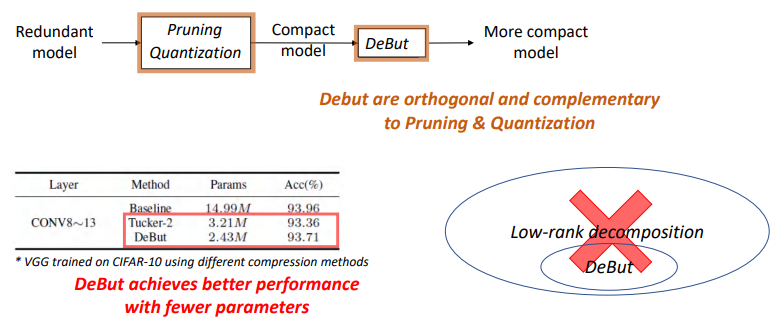
DeBut vs. Conventional Compression Schemes

我们还讨论了DeBut与目前非常流行的压缩方案之间的关系，大致分为量化、剪枝等。对于量化和剪枝，我们强调DeBut与其是互补的，因为DeBut可以进一步压缩。

DeBut是一种全新的高吸收度的结构矩阵因式分解方式。

Conclusion

● DeBut层是真正实用的，可以在很复杂的数据集和较大的网络中实现。

● DeBut本质上与卷积层是不同的

● DeBut进一步同质化了全连接层和卷积层，以更低的复杂度突破了标准Butterfly矩阵2的n次方限制

● 两种DeBut chain是为了满足不同模型的要求，即compression ability, performance和stability的需求。

● DeBut factor product chain为管道化推理中的DNN加速带了很重要的启示。

提

醒

论文题目：

Deformable Butterfly: A Highly Structured and Sparse Linear Transform

论文链接：

https://proceedings.neurips.cc/paper/2021/hash/86b122d4358357d834a87ce618a55de0-Abstract.html

点击“阅读原文”，即可观看本场回放

整理：林  则

作者：林  睿

往期精彩文章推荐

记得关注我们呀！每天都有新知识！

 关于AI TIME 

AI TIME源起于2019年，旨在发扬科学思辨精神，邀请各界人士对人工智能理论、算法和场景应用的本质问题进行探索，加强思想碰撞，链接全球AI学者、行业专家和爱好者，希望以辩论的形式，探讨人工智能和人类未来之间的矛盾，探索人工智能领域的未来。

迄今为止，AI TIME已经邀请了700多位海内外讲者，举办了逾350场活动，超280万人次观看。

我知道你

在看

哦

~

点击 阅读原文 查看回放！