当前位置:网站首页>扩展卡尔曼滤波【转】
扩展卡尔曼滤波【转】
2022-08-03 00:55:00 【light169】
1、重点看【SLAM中的EKF,UKF,PF原理简介 - 半闲居士 - 博客园】
2、机器人重点看【定位(一):扩展卡尔曼滤波_windSeS的博客】
3、重点实例【扩展卡尔曼滤波(EKF)理论讲解与实例(matlab、python和C++代码)】
转自【扩展卡尔曼滤波_菜鸟知识搬运工的博客-CSDN博客_扩展卡尔曼滤波】
扩展卡尔曼滤波(Extended Kalman Filter,EKF)是标准卡尔曼滤波在非线性情形下的一种扩展形式,EKF算法是将非线性函数进行泰勒展开,省略高阶项,保留展开项的一阶项,以此来实现非线性函数线性化,最后通过卡尔曼滤波算法近似计算系统的状态估计值和方差估计值,对信号进行滤波。
一、泰勒级数展开
泰勒级数展开是将一个在 处具有
处具有 阶导数的函数
阶导数的函数 ,利用关于
,利用关于 的
的 次多项式逼近函数值的方法。
次多项式逼近函数值的方法。
若函数 在包含
在包含 的某个闭区间
的某个闭区间![[a,b]](http://img.inotgo.com/imagesLocal/202112/13/202112131930506399_2.gif) 上具有
上具有 阶导数,且在开区间
阶导数,且在开区间 上具有
上具有 阶导数,则对闭区间
阶导数,则对闭区间![[a,b]](http://img.inotgo.com/imagesLocal/202112/13/202112131930506399_2.gif) 上的任意一点
上的任意一点 ,都有:
,都有:
![]()
其中 表示函数
表示函数 在
在 处的
处的 阶导数,等式右边成为泰勒展开式,剩余的
阶导数,等式右边成为泰勒展开式,剩余的 是泰勒展开式的余项,是
是泰勒展开式的余项,是 的高阶无穷小。
的高阶无穷小。
当变量是多维向量时,一维的泰勒展开就需要做拓展,具体形式如下:
![]()
其中,![{{[\nabla f({{\mathbf{x}}_{k}})]}^{T}}={{\mathbf{J}}_{F}}](http://img.inotgo.com/imagesLocal/202208/03/202208030055346660_13.gif) 表示雅克比矩阵,
表示雅克比矩阵, 表示海塞矩阵,
表示海塞矩阵, 表示高阶无穷小。
表示高阶无穷小。
![{[\nabla f({{\bf{x}}})]^T} = {{\bf{J}}({\bf x})} = \begin{bmatrix} \frac{\partial f({\bf x})_1}{\partial {\bf x}_1} & \hdots & \frac{\partial f({\bf x})_1}{\partial {\bf x}_n}\\ \vdots & \ddots & \vdots \\ \frac{\partial f({\bf x})_m}{\partial {\bf x}_1} & \hdots & \frac{\partial f({\bf x})_m}{\partial {\bf x}_n} \end{bmatrix}](http://img.inotgo.com/imagesLocal/202208/03/202208030055346660_35.gif)
这里, 为
为 维,
维, 状态向量为
状态向量为 维,
维, 。
。
一般来说,EKF在对非线性函数做泰勒展开时,实际应用只取到一阶导,同样也能有较好的结果。取一阶导时,状态转移方程和观测方程就近似为线性方程,高斯分布的变量经过线性变换之后仍然是高斯分布,这样就能够延用标准卡尔曼滤波的框架。
二、扩展卡尔曼滤波EKF
标准卡尔曼滤波KF的状态转移方程和观测方程为


扩展卡尔曼滤波EKF的状态转移方程和观测方程为:
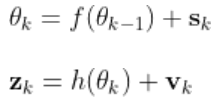
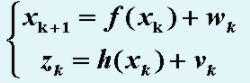 ,
,
利用泰勒展开式对上式在上一次的估计值处 (估计值)展开得
(估计值)展开得
![]() ,
,![]()
再利用泰勒展开式,在本轮的状态预测值处 展开得
展开得
![]() ,
, ![]()
其中, 和
和 分别表示函数
分别表示函数 和
和 在
在 和
和 处的雅克比矩阵。
处的雅克比矩阵。
(注:这里对泰勒展开式只保留到一阶导,二阶导数以上的都舍去,噪声假设均为加性高斯噪声)
基于以上的公式,给出EKF的预测(Predict)和更新(Update)两个步骤:
Propagation:


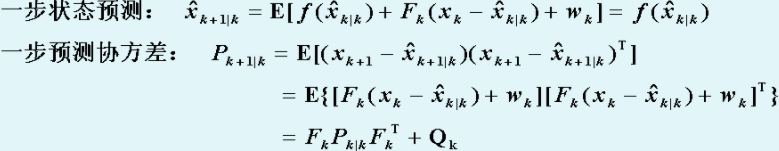
Update:




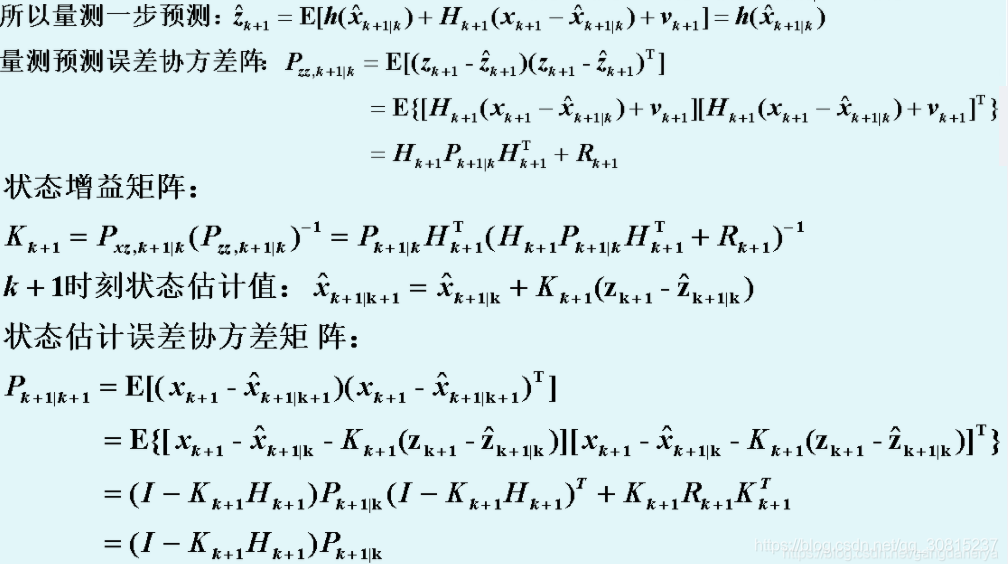
其中的雅克比矩阵和分别为
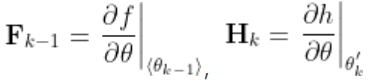 (H的导数只能在预测值处取,因为这个时候你还不知道估计值,是先有k时刻的H,然后有K,最后才有k时刻的估计值)
(H的导数只能在预测值处取,因为这个时候你还不知道估计值,是先有k时刻的H,然后有K,最后才有k时刻的估计值)
雅可比矩阵的计算,在MATLAB中可以利用对自变量加上一个eps(极小数),然后用因变量的变化量去除以eps即可得到雅可比矩阵的每一个元素值。
from :卡尔曼滤波系列——(二)扩展卡尔曼滤波_GHelpU的博客-CSDN博客_扩展卡尔曼滤波算法
from :扩展卡尔曼滤波(EKF)算法详细推导及仿真(Matlab)_钢蛋_小朋友的博客-CSDN博客_ekf算法
这是书上给出的一个例子,我希望从中能归纳一种套路可以用在 大部分EKF问题中
一:建立数学模型
(一):建立状态方程
状态方程是由具体问题的物理意义抽象出来的,不同问题具有不同的状态方程,是已知量。
(二):建立观测方程
观测方程也是由实际物理意义抽象出来的,已知量。
(三):一阶线性化状态方程,求状态转移矩阵F(k)。(其实就是把状态方程求偏导的过程)
(四):一阶线性化观测方程,求解观测矩阵H(k)
接下来进入卡尔曼滤波,首先时间更新
(五):状态预测
EKF的状态预测和KF的状态预测其实没有差别,都是假设没有过程噪声w,然后使用状态方程将上一时刻的后验估计值代入,X(k|k-1)是指用k-1时刻估计出来的k时刻的值,也即k时刻的先验估计值,同理X(k-1|k-1)就是指k-1时刻的后验估计值
(六):观测预测(下面状态更新时要用)
说实话当时看参考书这里一直没看懂,y不应该是传感器测出来的值吗,为什么要预测?这里我的理解是,“预测”指的是第5步的预测,这里只是把预测结果转化到测量度量下。
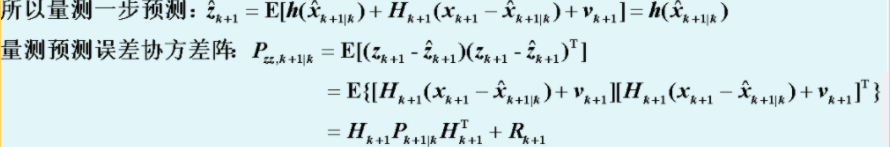
(七):求协方差预测,EKF的协方差预测和KF也是基本没差别,只不过是F(k)需要用偏导先求出来
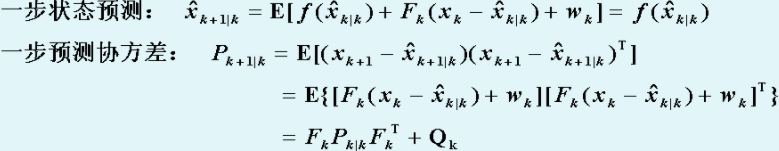
接下来进入状态更新
(八):求卡尔曼滤波增益
(九):求状态后验估计值
![]()
(十):协方差更新
至此,卡尔曼滤波需要的所有方程推导完毕,从(三)到(十)为一次EKF迭代
from:卡尔曼滤波(5):一种用EKF解决问题的思路_buaazyp的博客-CSDN博客
雅克比矩阵计算参考扩展卡尔曼滤波(EKF)理论讲解与实例(matlab、python和C++代码)(有空记得看这篇博文)
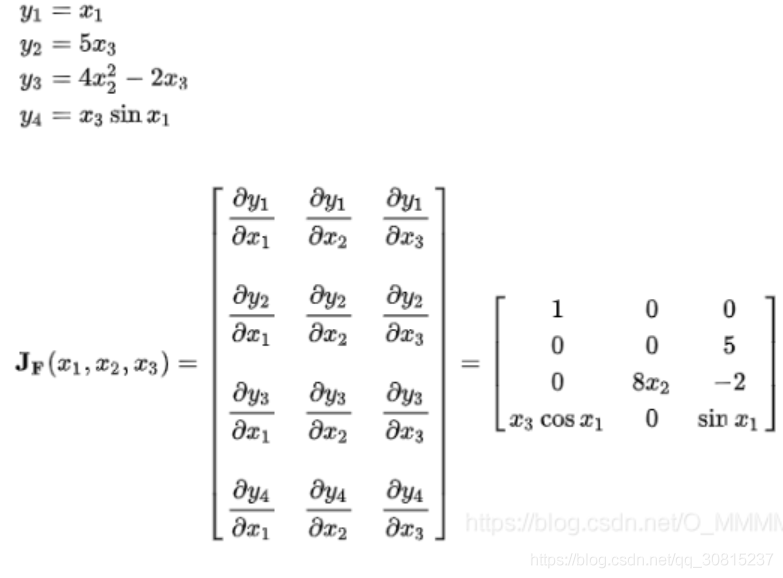
matlab示例:
% author : Perry.Li @USTC
% function: simulating the process of EKF
% date: 04/28/2015
%
N = 50; %计算连续N个时刻
n=3; %状态维度
q=0.1; %过程标准差
r=0.2; %测量标准差
Q=q^2*eye(n); %过程方差
R=r^2; %测量值的方差
[email protected](x)[x(2);x(3);0.05*x(1)*(x(2)+x(3))]; %状态方程
[email protected](x)[x(1);x(2);x(3)]; %测量方程
s=[0;0;1]; %初始状态
%初始化状态
x=s+q*randn(3,1);
P = eye(n);
xV = zeros(n,N);
sV = zeros(n,N);
zV = zeros(n,N);
for k=1:N
z = h(s) + r*randn;
sV(:,k)= s; %实际状态
zV(:,k) = z; %状态测量值
[x1,A]=jaccsd(f,x); %计算f的雅可比矩阵,其中x1对应黄金公式line2
P=A*P*A'+Q; %过程方差预测,对应line3
[z1,H]=jaccsd(h,x1); %计算h的雅可比矩阵
K=P*H'*inv(H*P*H'+R); %卡尔曼增益,对应line4
x=x1+K*(z-z1); %状态EKF估计值,对应line5
P=P-K*H*P; %EKF方差,对应line6
xV(:,k) = x; %save
s = f(s) + q*randn(3,1); %update process
end
for k=1:3
FontSize=14;
LineWidth=1;
figure();
plot(sV(k,:),'g-'); %画出真实值
hold on;
plot(xV(k,:),'b-','LineWidth',LineWidth) %画出最优估计值
hold on;
plot(zV(k,:),'k+'); %画出状态测量值
hold on;
legend('真实状态', 'EKF最优估计估计值','状态测量值');
xl=xlabel('时间(分钟)');
t=['状态 ',num2str(k)] ;
yl=ylabel(t);
set(xl,'fontsize',FontSize);
set(yl,'fontsize',FontSize);
hold off;
set(gca,'FontSize',FontSize);
end
function [z,A]=jaccsd(fun,x)
% JACCSD Jacobian through complex step differentiation
% [z J] = jaccsd(f,x)
% z = f(x)
% J = f'(x)
%
z=fun(x);
n=numel(x);
m=numel(z);
A=zeros(m,n);
h=n*eps;
for k=1:n
x1=x;
x1(k)=x1(k)+h*i;
A(:,k)=imag(fun(x1))/h;
end边栏推荐
猜你喜欢
【SQL】—数据库操作、表操作
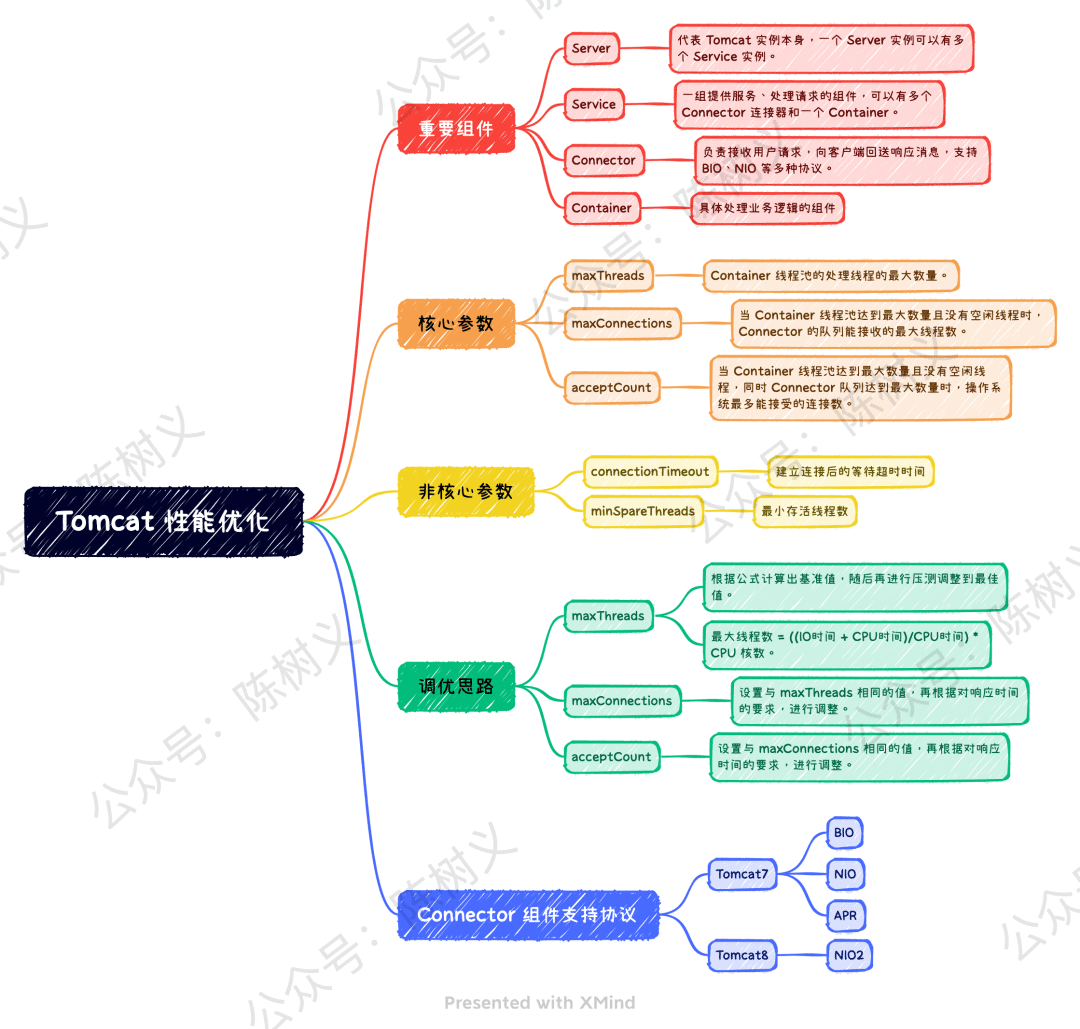
接口流量突增,如何做好性能优化?
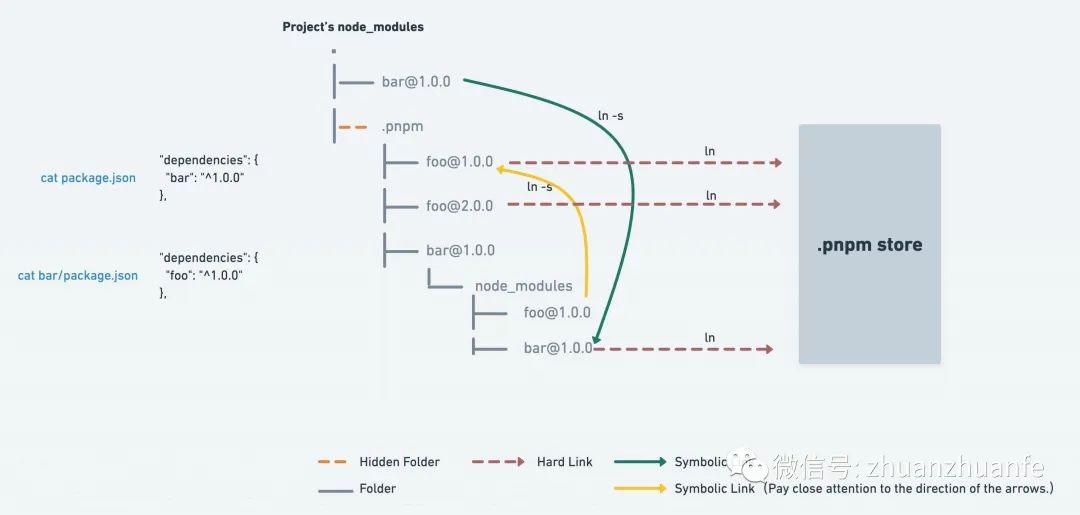
从 npm 切换到 pnpm,真香!

个人开发者必备,免费 API 网关工具推荐
2022年8月2日——使用idea搭建servlet+jsp项目

麒麟信安邀您抢先看 | openEuler 志高远,开源汇智创未来-开放原子全球开源峰会欧拉分论坛最详细议程出炉
软件测试从业多年,自认为技术不错,裸辞:一晃 ,失业3个月了~
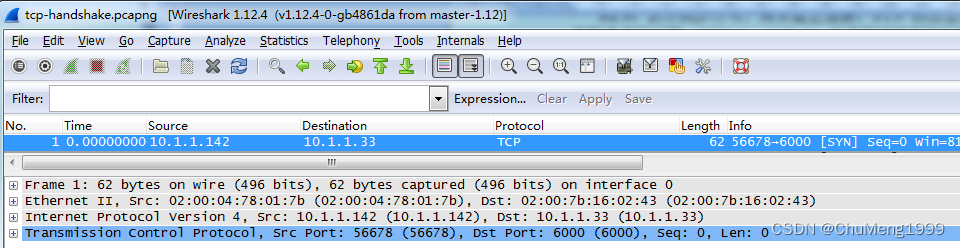
Wireshark data capture and analysis of the transport layer protocol (TCP protocol)
关于地图GIS开发事项的一次实践整理(上)

matlab常微分方程在传染病建模中的应用
随机推荐
2149. 按符号重排数组
SAP ABAP Gateway Client 里 OData 测试的 PUT, PATCH, MERGE 请求有什么区别
v-if、v-else、v-elseif v-show v-for
Introduction to agile development
Vite教程 安装
封装和练习题目
Brute force recursion to dynamic programming 07 (516. Longest palindrome subsequence)
WRF-Chem模式调试、运行、结果后处理等遇到的各种问题
torchvision.datasets.ImageFolder使用详解
PyCharm中常用的快捷键用法详解
npm运行项目dependencies were not found: core-js/modules/es6.array.fill
7.31
使用VSCode中遇到的问题及解决办法
图文详细解决IDEA使用Debug模式启动项目一直转圈圈跑起不来(亲测可以)
【SQL】—数据库操作、表操作
Jenkins汉化设置
从一文中了解SSRF的各种绕过姿势及攻击思路
并发模型和I/O模型介绍
嵌入式开发:嵌入式基础——’ ’和” ”的区别
Qt在选择MSVC 编译器的时候,无法识别出M_PI的问题处理