当前位置:网站首页>"NIO Cup" 2022 Nioke Summer Multi-School Training Camp 4 DHKLN
"NIO Cup" 2022 Nioke Summer Multi-School Training Camp 4 DHKLN
2022-07-30 22:54:00 【HeartFireY】
D.Jobs (Easy Version)
题目大意
三维偏序问题,Teammates wrote a fake practice.
待补
Code
#include <bits/stdc++.h>
#pragma gcc optimize("O2")
#pragma g++ optimize("O2")
//#define int long long
#define endl '\n'
using namespace std;
const int N = 2e5 + 10, MOD = 998244353;
int n, q, x, y, z;
int k1,k2,k3,k4;
bitset<402>fk[11][401][401];
inline int getid(int x,int y,int z){
return 160801*(x)+(y)*(401)+z;
}
int getans(int iq, int eq, int aq){
int ans=0;
for(int i=1;i<=n;i++){
ans+=fk[i][iq][eq][aq];
}
return ans;
}
int binpow(long long x, int y, int mod, long long res = 1){
for (; y; y >>= 1, (x *= x) %= mod) if (y & 1) (res *= x) %= mod;
return res;
}
int powq[2000010];
inline void solve(){
cin >> n >> q;
for(int i = 1; i <= n; i++){
cin >> k1;
for(int j = 1; j <= k1; j++) {
cin>>x>>y>>z;
fk[i][x][y][z]=1;
}
}
for(short i=1;i<=n;i++){
for(short j=1;j<=400;j++){
for(short k=1;k<=400;k++){
for(short x=1;x<=400;x++){
fk[i][j][k][x]=fk[i][j][k][x]|fk[i][j][k][x-1]|fk[i][j][k-1][x]|fk[i][j-1][k][x];
}
}
}
}
int seed; cin >> seed;
powq[0] = 1;
for(int i = 1; i <= 2000000 + 5; i++){
powq[i] = 1ll * powq[i - 1] * seed % MOD;
}
std::mt19937 rng(seed);
std::uniform_int_distribution<> u(1, 400);
int lastans = 0, ans = 0;
for (int i = 1; i <= q; i++){
int IQ = (u(rng) ^ lastans) % 400 + 1; // The IQ of the i-th friend
int EQ = (u(rng) ^ lastans) % 400 + 1; // The EQ of the i-th friend
int AQ = (u(rng) ^ lastans) % 400 + 1; // The AQ of the i-th friend
lastans = getans(IQ, EQ, AQ); // The answer to the i-th friends
(ans += (1ll * lastans * powq[q - i] % MOD)) %= MOD;
}
cout << (ans % MOD) << endl;
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
cout << fixed << setprecision(12);
int t = 1;
while(t--) solve();
return 0;
}
H.Wall Builder II
题目大意
给 n n n个 1 ∗ 1 1*1 1∗1的矩形, n − 1 n-1 n−1个 1 ∗ 2 1*2 1∗2的矩形, n − 2 n-2 n−2个 1 ∗ 3 1*3 1∗3的矩形…, 1 1 1个 1 ∗ n 1*n 1∗n的矩形,Piece these rectangles together into one big rectangle,Find the minimum perimeter of a large rectangle.
从 s \sqrt{s} s开始枚举,Then find the first rectangle that can be made up and fill it greedily.
Code
#include <bits/stdc++.h>
#pragma gcc optimize("O2")
#pragma g++ optimize("O2")
#define int long long
#define endl '\n'
using namespace std;
const int N = 2e4 + 10, MOD = 1e9 + 7;
int row[N];
inline void solve(){
int n = 0, s = 0; cin >> n;
memset(row, 0, sizeof(row));
for(int i = 1; i <= n; i++) s += (n - i + 1) * i;
for(int w = sqrt(s); w <= s; w++){
if(s % w) continue;
int h = s / w;
cout << (h + w) * 2 << endl;
for(int i = n; i >= 1; --i){
for(int j = 1, id = 0; j <= n - i + 1;){
if(row[id] + i <= w){
cout << row[id] << ' ' << id << ' ' << row[id] + i << ' ' << id + 1 << endl;
row[id]+= i, j++;
}
else id++;
}
}
break;
}
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
cout << fixed << setprecision(12);
int t = 1; cin >> t;
while(t--) solve();
return 0;
}
K.NIO’s Sword
题目大意
The player initially has an attack power of 0 0 0的剑,Need to kill in sequence n n n个敌人,Only when attack power mod n n n与 i i iCongruence to kill the first i i i个敌人.Players can upgrade swords,Each upgrade is equivalent to adding a number to the current attack power,Ask at least a few upgrades.
对每个 i i i,枚举 k i k_i ki,计算 x i x_i xi,It is enough to judge whether it is satisfied.
Code
#include <bits/stdc++.h>
#pragma gcc optimize("O2")
#pragma g++ optimize("O2")
#define int long long
#define endl '\n'
using namespace std;
const int N = 2e5 + 10, MOD = 1e9 + 7;
int f[10];
inline void solve(){
int n; cin >> n;
int ans = 0;
f[0] = 1;
for(int i = 1; i < 8; ++i) f[i] = f[i - 1] * 10;
if(n == 1){
cout << "0\n";
return;
}
for(int i = 1; i <= n; ++i){
int tmp = i - 1;
for(int j = 1; j <= 7; ++j){
if(((i - tmp * f[j]) % n + n) % n < f[j]){
ans += j;
break;
}
}
}
cout << ans << "\n";
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
cout << fixed << setprecision(12);
int t = 1; //cin >> t;
while(t--) solve();
return 0;
}
L.Black Hole
题目大意
给定正 n n n面体(不一定合法,不合法就impossible),边长为 a a a,进行 k k k次操作,Each operation takes the line connecting the geometric center of the regular polyhedron to generate a new convex hull.问 K K KWhether the resulting polyhedron is a regular polyhedron after this operation,and the edge lengths of the final regular polyhedron.
首先,Legal regular polyhedra only:正四面体、正六面体、正八面体、正十二面体、正二十面体.
- Regular tetrahedra can only generate regular tetrahedra
- Regular hexahedron operations can be performed an odd number of times to generate regular octahedrons,The regular hexahedron is generated evenly
- Regular octahedron operations can be performed an odd number of times to generate regular hexahedrons,The regular octahedron is generated evenly
- An icosahedron can be generated by doing an odd number of dodecahedron operations,Generates a regular dodecahedron even number of times
- A regular icosahedron can be generated by performing an odd number of operations on a regular icosahedron,Generates a regular icosahedron an even number of times
Next, we discuss the law of side length variation:It can be found that the side length relationship of the two generation can be derived from the inscribed sphere of the original body and the circumscribed sphere of the generated body,Because the two balls are the same ball.So first, let's sort out the side lengths a a awith the sphere radius r r r关系公式:
| 正四面体 | 正六面体 | 正八面体 | 正十二面体 | 正二十面体 | |
|---|---|---|---|---|---|
| Inside the ball | r a = 6 12 \frac{r}{a} = \frac{\sqrt{6}}{12} ar=126 | r a = 1 2 \frac{r}{a} = \frac{1}{2} ar=21 | r a = 6 6 \frac{r}{a} = \frac{\sqrt{6}}{6} ar=66 | r a = φ 2 2 3 − φ \frac{r}{a} = \frac{\varphi^2}{2\sqrt{3 - \varphi}} ar=23−φφ2 | r a = 3 3 + 15 12 \frac{r}{a} = \frac{3\sqrt{3} + \sqrt{15}}{12} ar=1233+15 |
| receiver | r a = 6 4 \frac{r}{a} = \frac{\sqrt{6}}{4} ar=46 | r a = 3 2 \frac{r}{a} = \frac{\sqrt{3}}{2} ar=23 | r a = 2 2 \frac{r}{a} = \frac{\sqrt{2}}{2} ar=22 | r a = 3 φ 2 \frac{r}{a} = \frac{\sqrt{3} \varphi}{2} ar=23φ | r a = 10 + 2 5 4 \frac{r}{a} = \frac{\sqrt{10 + 2\sqrt{5}}}{4} ar=410+25 |
Then we can deduce the transformation relation:
- 正四面体 → \rightarrow →正四面体: a 2 a 1 = 1 3 \frac{a_2}{a_1} = \frac{1}{3} a1a2=31
- 正六面体 → \rightarrow →正八面体: a 2 a 1 = 1 2 \frac{a_2}{a_1} = \frac{1}{\sqrt{2}} a1a2=21
- 正八面体 → \rightarrow →正六面体: a 2 a 1 = 2 3 \frac{a_2}{a_1} = \frac{\sqrt{2}}{3} a1a2=32
- 正十二面体 → \rightarrow →正二十面体: a 2 a 1 = φ 2 3 − φ × 2 5 + 10 \frac{a_2}{a_1} = \frac{\varphi^2}{\sqrt{3 - \varphi} \times \sqrt{2 \sqrt{5} + 10}} a1a2=3−φ×25+10φ2
- 正二十面体 → \rightarrow →正十二面体: a 2 a 1 = 5 + 3 6 φ \frac{a_2}{a_1} = \frac{\sqrt{5} + 3}{6 \varphi} a1a2=6φ5+3
至此,The answer can be obtained by recursion.
Code
#include <bits/stdc++.h>
#pragma gcc optimize("O2")
#pragma g++ optimize("O2")
#define int long long
#define double long double
#define endl '\n'
using namespace std;
const int N = 2e5 + 10, MOD = 1e9 + 7;
double K[20];
int nxt[20], n, k;
double a;
void init(){
cout << fixed << setprecision(12);
K[4] = 1.0 / 3;
double fi = (1 + sqrtl(5)) / 2;
K[6] = sqrtl(2) / 2;
K[8] = sqrtl(2) / 3;
K[12] = 2 * fi / sqrtl(3 - fi) * fi / sqrtl(10 + 2 * sqrtl(5));
K[20] = (3 + sqrtl(5)) / 6 / fi;
nxt[4] = 4, nxt[6] = 8, nxt[8] = 6, nxt[12] = 20, nxt[20] = 12;
}
inline void solve(){
cin >> n >> a >> k;
if(n != 4 && n != 6 && n != 8 && n != 12 && n != 20){
cout << "impossible\n";
return;
}
for(int i = 1; i <= k; i++){
a *= K[n], n = nxt[n];
}
cout << "possible "<<n<<" "<<a<<endl;
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
init();
int t = 1; cin >> t;
while(t--) solve();
return 0;
}
N.Particle Arts
题目大意
给定序列 a 1 , a 2 , … , a n a_1, a_2, \dots, a_n a1,a2,…,an,whenever two elements a a a和 b b bWhen collided, they annihilate and create two new elements a & b a \& b a&b和 a ∣ b a | b a∣b.after several collisions,The variance will converge.Find the variance after convergence.
首先可以发现,After any two elements collide and change,Does not cause a change in the sum,因此The mean is unchanged.
Then consider finding the new sequence generated after infinite such collisions,Easy to spot because of or the nature of the operation,二进制下为 1 1 1The bits will not disappear,Then the infinite OR operation will be 1 1 1的位move closer to the same number.Therefore, a new sequence calculation can be generated directly after the bitwise statistics.
如果使用公式 E ( x 2 ) − E 2 ( x ) E(x^2) - E^2(x) E(x2)−E2(x),Need to keep pushing;But you can go directly to the variance formula,But it will explodelong long,Then it can be used in all operations__int128计算,最后转long long输出.
Code
#include <bits/stdc++.h>
#pragma gcc optimize("O2")
#pragma g++ optimize("O2")
#define int __int128
#define endl '\n'
using namespace std;
const int N = 2e5 + 10, MOD = 1e9 + 7;
long long a[N], b[N], cnt[20];
inline void solve(){
long long n = 0, sum = 0; cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i], sum += a[i];
int cnt0 = 0, cnt1 = 0;
for(int i = 1; i <= n; i++){
for(int j = 0; j < 15; j++){
if((a[i] >> j) & 1) cnt[j]++;
}
}
for(int i = 0; i < 15; i++){
for(int j = 1; j <= cnt[i]; j++) b[j] |= (1 << i);
}
int f1 = 0;
for(int i = 1; i <= n; i++){
f1 += (n * b[i] - sum) * (n * b[i] - sum);
}
int f2 = n * n * n;
int gcdd = __gcd(f1, f2);
//cout << f1 << '@' << f2 << endl;
long long ans1 = f1 / gcdd, ans2 = f2 / gcdd;
//cout << (f1 / gcdd) << '/' << (f2 / gcdd) << endl;
cout << ans1 << '/' << ans2 << endl;
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
cout << fixed << setprecision(12);
int t = 1; //cin >> t;
while(t--) solve();
return 0;
}
边栏推荐
猜你喜欢
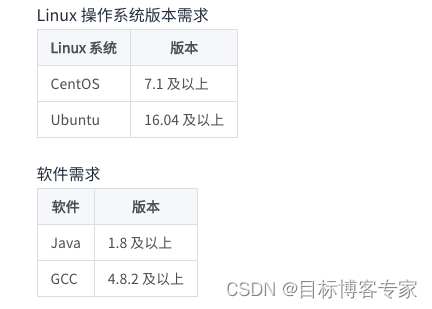
Apache Doris系列之:安装与部署详细步骤
PS基础学习(一)

Mysql进阶优化篇01——四万字详解数据库性能分析工具(深入、全面、详细,收藏备用)
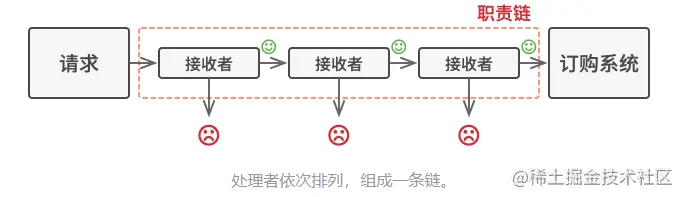
代码越写越乱?那是因为你没用责任链

反转链表-头插反转法

使用LVS和Keepalived搭建高可用负载均衡服务器集群

# Dasctf 7月赋能赛 WP

MySQL 5.7详细下载安装配置教程

Abstract classes and interfaces (study notes)

ML之shap:基于FIFA 2018 Statistics(2018年俄罗斯世界杯足球赛)球队比赛之星分类预测数据集利用RF随机森林+计算SHAP值单样本力图/依赖关系贡献图可视化实现可解释性之攻略
随机推荐
HF2022-EzPHP复现
2022/07/30 学习笔记 (day20) 面试题积累
语言代码表
代码越写越乱?那是因为你没用责任链
阿里云视频点播+项目实战
reindex win10
Day016 类和对象
只会纯硬件,让我有点慌
第十九周进度(了解物联网基础知识)
一文详解:SRv6 Policy模型、算路及引流
CISP-PTE Zhenti Demonstration
2sk2225 Substitute 3A/1500V Chinese Documentation【PDF Data Book】
cookie和session区别
【云驻共创】HCSD大咖直播–就业指南
【无标题】
A detailed explanation: SRv6 Policy model, calculation and drainage
cnpm安装步骤
2022.7.28
Apache Doris系列之:安装与部署详细步骤
[MySQL] DQL related operations