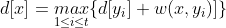当前位置:网站首页>格林公式挖洞法中内曲线顺时针的直观解释
格林公式挖洞法中内曲线顺时针的直观解释
2022-06-23 22:16:00 【深海里的鱼(・ω<)*】
视频讲解:格林公式挖洞法中内曲线顺时针的直观解释
使用格林公式的时候,取曲线逆时针为正方向,但如果曲线包围的区域内存在奇点,则不能直接使用格林公式,需要先使用挖洞法,其中内曲线为顺时针,大家记忆口诀通常是“外逆内顺”,如图所示,A为平面上的奇点
当然曲线可能并不像图示那么光滑,可能是凹凸不平,比如这样
为了作图简单,本文将使用较为简单的曲面
那么为什么内曲线是顺时针呢,本文给大家一个直观的解释。
先来看一个这样的曲面,围成的区域为黄色部分,如图所示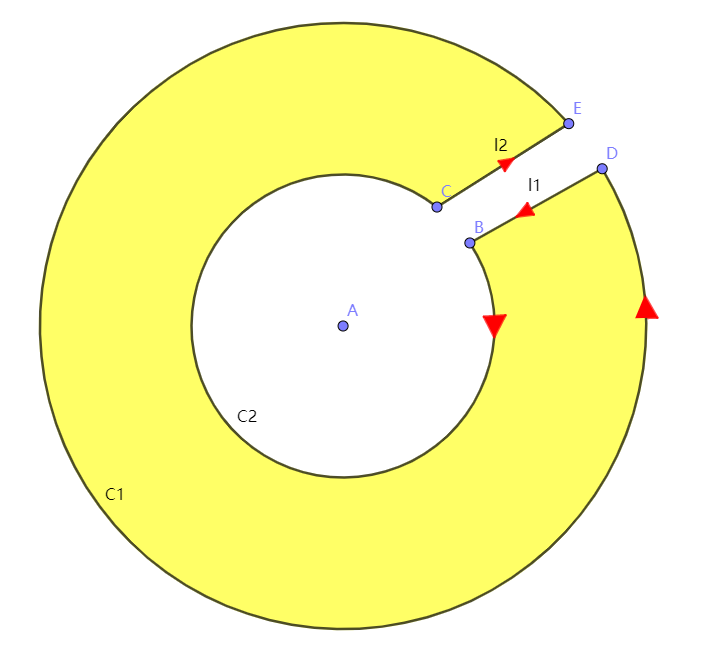
此区域不包含奇点,所以可以放心的使用格林公式
∮ C = ∫ C 1 + ∫ l 1 + ∫ C 2 + ∫ l 2 = ∬ D \oint_C{}=\int_{C1}{}+\int_{l1}{}+\int_{C2}{}+\int_{l2}{}=\iint_D{} ∮C=∫C1+∫l1+∫C2+∫l2=∬D
我们将点B和C,点D和E逐渐靠近,直到重合,如图所示
此时 l 1 l1 l1和 l 2 l2 l2重合,方向相反,则
∫ l 1 + ∫ l 2 = 0 \int_{l1}{}+\int_{l2}{}=0 ∫l1+∫l2=0
所以
∮ C = ∫ C 1 + ∫ l 1 + ∫ C 2 + ∫ l 2 = ∫ C 1 + ∫ C 2 = ∬ D \oint_C{}=\int_{C1}{}+\int_{l1}{}+\int_{C2}{}+\int_{l2}{}=\int_{C1}{}+\int_{C2}{}=\iint_D{} ∮C=∫C1+∫l1+∫C2+∫l2=∫C1+∫C2=∬D
所以我们可以将 l 1 l1 l1和 l 2 l2 l2去掉
所以最后可以得出
∮ C 1 + C 2 = ∬ D \oint_{C1+C2}{}=\iint_D{} ∮C1+C2=∬D
边栏推荐
- 嵌入式接口复习资料
- Stm32 - - - - interruption externe
- 1004. number of maximum consecutive 1 III ●●
- Short video enters the hinterland of online music
- Embedded interface review materials
- Flutter中的GetX状态管理用起来真的那么香吗?
- PyQt5_QTableWidget分页单选右键菜单控件
- Kotlin set list, set, map operation summary
- Golang 类型断言
- 国内外最好的12款项目管理系统优劣势分析
猜你喜欢
随机推荐
Task queue of laravel
PyQt5_QTableWidget分页单选右键菜单控件
在OpenCloudOS使用snap安装.NET 6
AutoCAD -- summarize three methods of drawing rounded corners in CAD
The lower left corner of vs QT VTK displays the synchronized minor coordinate axis
3D打印和激光切割流程的初步了解
BroadcastReciver 和LocalBroadcastManager区别
6、STM32——串口数据收发基础
Bitmap加载内存分析
Several cases of index invalidation caused by MySQL
A cartoon reading app highly imitating Tencent comics
Is the geTx status management in the flutter really so good to use?
Is Everbright futures safe? What do I need to open an account?
IDEA 自动生成单元测试,效率倍增!
E: 无法获得锁 /var/lib/dpkg/lock
【Try to Hack】masscan
关于H5移动端用什么自动化测试
2018/GAN:Self-Attention Generative Adversarial Networks自我注意生成对抗网络
思考(八十七):协议加密与压缩
"Shanda Diwei Cup" the 12th Shandong ICPC undergraduate program design competition