当前位置:网站首页>Machine learning notes - building a recommendation system (4) matrix decomposition for collaborative filtering
Machine learning notes - building a recommendation system (4) matrix decomposition for collaborative filtering
2022-07-25 03:19:00 【Sit and watch the clouds rise】
One 、 Overview of collaborative filtering
Collaborative filtering is the core of any modern recommendation system , It's on Amazon 、Netflix and Spotify And the company has achieved considerable success . It works by collecting human judgments of items in a given domain ( Called rating ), And match people with the same information needs or tastes . Users of collaborative filtering system share their analysis, judgment and opinions on each item they consume , So that other users of the system can better decide which items to consume . In return , Collaborative filtering system provides useful personalized recommendations for new projects .

The two main areas of collaborative filtering are (1) Neighborhood method and (2) Potential factor model .
- Neighborhood method Focus on computing relationships between projects or users . This method evaluates users' preferences for items based on the same user's rating of adjacent items . The neighbor of a project is other products , When rated by the same user , They tend to get similar scores .
- Potential factor approach The scoring is explained by characterizing items and users by many factors inferred from the scoring pattern . for example , In music recommendation , The factors found may measure precise dimensions , For example, hip hop and jazz 、 The number of treble or the length of song , And less explicit dimensions , For example, the meaning behind the lyrics , Or completely unexplainable dimensions . For the user , Each factor measures the degree to which users like songs with high scores on the corresponding song factors .
Some of the most successful potential factor models are based on Matrix decomposition . In its natural form , Matrix decomposition uses factor vectors inferred from project rating patterns to characterize projects and users . The high correspondence between project and user factors leads to recommendations .

Two 、Vanilla Matrix Factorization
A simple matrix decomposition model maps users and projects to dimensions D Joint potential factor space — So the user - The interaction of the project is modeled as the inner product in the space .
- therefore , Each project i And vector q_i Related to , And every user u And vector p_u Related to .
- For a given project i,q_i The element of measures the extent to which the project has these factors , Whether it's positive or negative .
- For a given user u,p_u The elements measure the user's response to the corresponding factors ( Positive or negative ) High degree of interest in the project .
- The dot product obtained (q_i * p_u) Captured users u And projects i Interaction between , That is, the overall interest of users in the characteristics of the project .
therefore , We have the following equation 1:

The biggest challenge is to calculate the factor vector for each project and user q_i and p_u Mapping . Matrix factorization does this by minimizing the regularized square error on a known rating set , As shown in the following equation 2 Shown :

The model is learned by fitting previously observed ratings . However , The goal is to predict the future / Unknown ratings summarize these previous ratings . therefore , We want to add L2 Regularization penalty to avoid over fitting observed data , And optimize the learning parameters at the same time with random gradient descent .
When we use SGD When fitting the parameters of the model to the learning problem at hand , We take a step in solution space towards the gradient of loss function relative to network parameters in each iteration of the algorithm . Because we recommend users - The project interaction matrix is very sparse , This learning method may over fit the training data .
L2 It is a specific method to regularize the cost function by adding complexity representation . This term is the square Euclidean norm of the potential factors of users and projects . Added an additional parameter λ To allow you to control the intensity of regularization . add to L2 Items usually result in smaller parameters for the entire model .
import torch
from torch import nn
import torch.nn.functional as F
class MF(nn.Module):
def __call__(self, train_x):
# These are the user indices, and correspond to "u" variable
user_id = train_x[:, 0]
# These are the item indices, correspond to the "i" variable
item_id = train_x[:, 1]
# Initialize a vector user = p_u using the user indices
vector_user = self.user(user_id)
# Initialize a vector item = q_i using the item indices
vector_item = self.item(item_id)
# The user-item interaction: p_u * q_i is a dot product between the 2 vectors above
ui_interaction = torch.sum(vector_user * vector_item, dim=1)
return ui_interaction
def loss(self, prediction, target):
# Calculate the Mean Squared Error between target = R_ui and prediction = p_u * q_i
loss_mse = F.mse_loss(prediction, target.squeeze())
# Compute L2 regularization over user (P) and item (Q) matrices
prior_user = l2_regularize(self.user.weight) * self.c_vector
prior_item = l2_regularize(self.item.weight) * self.c_vector
# Add up the MSE loss + user & item regularization
total = loss_mse + prior_user + prior_item
return total3、 ... and 、 Matrix decomposition with deviation
One advantage of the matrix decomposition method of collaborative filtering is its flexibility in dealing with various data and other application specific requirements . Think about it , equation 1 Try to capture the interaction between users and items that produce different rating values . However , Most of the observed changes in rating values are due to user - or project related impacts , be called deviation , Not related to any interaction . The intuition behind this is , Some users give higher comments than others , And some projects have been systematically evaluated higher than other users .
therefore , We can put the equation 1 Extend to equation 3, As shown below :

- The deviation involved in the overall average score is b Express .
- Parameters w_i and w_u Respectively represent the observed items i And the user u Deviation from the average .
- Please note that , The observed scores are 4 Parts of :(1) user - Project interaction ,(2) Global average ,(3) Project deviation and (4) User bias .
The model is learned by minimizing a new square error function , As shown in the following equation 4 Shown :

import torch
from torch import nn
import torch.nn.functional as F
class MF(nn.Module):
def __call__(self, train_x):
# These are the user indices, and correspond to "u" variable
user_id = train_x[:, 0]
# These are the item indices, correspond to the "i" variable
item_id = train_x[:, 1]
# Initialize a vector user = p_u using the user indices
vector_user = self.user(user_id)
# Initialize a vector item = q_i using the item indices
vector_item = self.item(item_id)
# The user-item interaction: p_u * q_i is a dot product between the 2 vectors above
ui_interaction = torch.sum(vector_user * vector_item, dim=1)
# Pull out biases
bias_user = self.bias_user(user_id).squeeze()
bias_item = self.bias_item(item_id).squeeze()
biases = (self.bias + bias_user + bias_item)
# Add the bias to the user-item interaction to obtain the final prediction
prediction = ui_interaction + biases
return prediction
def loss(self, prediction, target):
# Calculate the Mean Squared Error between target and prediction
loss_mse = F.mse_loss(prediction, target.squeeze())
# Compute L2 regularization over the biases for user and the biases for item matrices
prior_bias_user = l2_regularize(self.bias_user.weight) * self.c_bias
prior_bias_item = l2_regularize(self.bias_item.weight) * self.c_bias
# Compute L2 regularization over user (P) and item (Q) matrices
prior_user = l2_regularize(self.user.weight) * self.c_vector
prior_item = l2_regularize(self.item.weight) * self.c_vector
# Add up the MSE loss + user & item regularization + user & item biases regularization
total = loss_mse + prior_user + prior_item + prior_bias_user + prior_bias_item
return total
Four 、 Matrix decomposition with edge characteristics
A common challenge of collaborative filtering is cold start , Because it can't handle new projects and new users . Or many users provide few scores , Make users - The project interaction matrix is very sparse . One way to alleviate this problem is to merge other sources of information about the user , Namely additional function . These can be user attributes ( Demography ) And implicit feedback .
Back to the example , Suppose I know the user's occupation . For this additional function , There are two choices : Add it as prejudice ( Artists like movies better than other professions ) And add it as a vector ( Real estate agents like real estate programs ). The matrix decomposition model should combine all signal sources with enhanced user representation , Like the equation 5 Shown :

- Professional deviation is used d_o Express , This means that career changes are the same as rates .
- The vector of occupation is t_o Express , This means that the profession will (q_i * t_o) And change .
- Please note that , Items can be treated similarly if necessary .
What does the loss function look like now ? The following formula 6 indicate :

import torch
from torch import nn
import torch.nn.functional as F
class MF(nn.Module):
def __call__(self, train_x):
# These are the user indices, and correspond to "u" variable
user_id = train_x[:, 0]
# These are the item indices, correspond to the "i" variable
item_id = train_x[:, 1]
# Initialize a vector user = p_u using the user indices
vector_user = self.user(user_id)
# Initialize a vector item = q_i using the item indices
vector_item = self.item(item_id)
# The user-item interaction: p_u * q_i is a dot product between the user vector and the item vector
ui_interaction = torch.sum(vector_user * vector_item, dim=1)
# Pull out biases
bias_user = self.bias_user(user_id).squeeze()
bias_item = self.bias_item(item_id).squeeze()
biases = (self.bias + bias_user + bias_item)
# These are the occupation indices, and correspond to "o" variable
occu_id = train_x[:, 3]
# Initialize a vector occupation = r_o using the occupation indices
vector_occu = self.occu(occu_id)
# The user-occupation interaction: p_u * r_o is a dot product between the user vector and the occupation vector
uo_interaction = torch.sum(vector_user * vector_occu, dim=1)
# Add the bias, the user-item interaction, and the user-occupation interaction to obtain the final prediction
prediction = ui_interaction + uo_interaction + biases
return prediction
def loss(self, prediction, target):
# Calculate the Mean Squared Error between target and prediction
loss_mse = F.mse_loss(prediction.squeeze(), target.squeeze())
# Compute L2 regularization over the biases for user and the biases for item matrices
prior_bias_user = l2_regularize(self.bias_user.weight) * self.c_bias
prior_bias_item = l2_regularize(self.bias_item.weight) * self.c_bias
# Compute L2 regularization over user (P) and item (Q) matrices
prior_user = l2_regularize(self.user.weight) * self.c_vector
prior_item = l2_regularize(self.item.weight) * self.c_vector
# Compute L2 regularization over occupation (R) matrices
prior_occu = l2_regularize(self.occu.weight) * self.c_vector
# Add up the MSE loss + user & item regularization + user & item biases regularization + occupation regularization
total = loss_mse + prior_user + prior_item + prior_bias_item + prior_bias_user + prior_occu
return total5、 ... and 、 Matrix decomposition with time characteristics
up to now , Our matrix decomposition model has always been static . In reality , The popularity of items and user preferences are constantly changing . therefore , We should consider reflecting users - The time effect of the dynamic nature of project interaction . To achieve this , We can add a time item that affects user preferences , Thus affecting the interaction between users and projects .
To mix a little , Let's try the following new formula 7, It includes time t Dynamic prediction rules of rating :

 Take the user factor as a function of time . On the other hand ,
Take the user factor as a function of time . On the other hand , remain unchanged , Because the project is static .
remain unchanged , Because the project is static .- According to the users (
 ) Make a career change .
) Make a career change .
equation 8 A new loss function with time characteristics is shown :

import torch
from torch import nn
import torch.nn.functional as F
class MF(nn.Module):
def __call__(self, train_x):
# These are the user indices, and correspond to "u" variable
user_id = train_x[:, 0]
# These are the item indices, correspond to the "i" variable
item_id = train_x[:, 1]
# These are the occupation indices, and correspond to "o" variable
occu_id = train_x[:, 3]
# Initialize a vector user = p_u using the user indices
vector_user = self.user(user_id)
# Initialize a vector item = q_i using the item indices
vector_item = self.item(item_id)
# Initialize a vector occupation = r_o using the occupation indices
vector_occu = self.occu(occu_id)
# Pull out biases
bias_user = self.bias_user(user_id).squeeze()
bias_item = self.bias_item(item_id).squeeze()
biases = (self.bias + bias_user + bias_item)
# The user-item interaction: p_u * q_i is a dot product between the user vector and the item vector
ui_interaction = torch.sum(vector_user * vector_item, dim=1)
# The user-occupation interaction: p_u * r_o is a dot product between the user vector and the occupation vector
uo_interaction = torch.sum(vector_user * vector_occu, dim=1)
# These are the rank indices
rank = train_x[:, 2]
# Initialize a vector temporal using the rank indices
vector_temp = self.temp(rank)
# Initialize a vector user-temporal using the user IDs
vector_user_temp = self.user_temp(user_id)
# The user-time interaction is a dot product between the user temporal vector and the temporal vector
ut_interaction = torch.sum(vector_user_temp * vector_temp, dim=1)
# Final prediction is the sum of all these interactions with the biases
prediction = ui_interaction + uo_interaction + ut_interaction + biases
return prediction
def loss(self, prediction, target):
# Calculate the Mean Squared Error between target and prediction
loss_mse = F.mse_loss(prediction.squeeze(), target.squeeze())
# Compute L2 regularization over the biases for user and the biases for item matrices
prior_bias_user = l2_regularize(self.bias_user.weight) * self.c_bias
prior_bias_item = l2_regularize(self.bias_item.weight) * self.c_bias
# Compute L2 regularization over user (P), item (Q), and occupation (R) matrices
prior_user = l2_regularize(self.user.weight) * self.c_vector
prior_item = l2_regularize(self.item.weight) * self.c_vector
prior_occu = l2_regularize(self.occu.weight) * self.c_vector
# Compute L2 regularization over temporal matrices
prior_ut = l2_regularize(self.user_temp.weight) * self.c_ut
# Compute total variation regularization over temporal matrices
prior_tv = total_variation(self.temp.weight) * self.c_temp
# Add up the MSE loss + user & item & occupation regularization + user & item biases regularization +
# temporal regularization + total variation
total = loss_mse + prior_user + prior_item + prior_ut + \
prior_bias_item + prior_bias_user + prior_occu + prior_tv
return total6、 ... and 、 Decomposer
A more powerful technology in the recommendation system is called Decomposer , It has powerful 、 Expression ability to summarize the matrix decomposition method . In many applications , We have a lot of project metadata that can be used to make better predictions . This is one of the benefits of using a factoring machine with feature rich data sets , There is a natural way to include additional features in the model , And you can use dimension parameters d Modeling high-order interactions . For sparse datasets , The second-order decomposition machine model is sufficient , Because there is not enough information to estimate more complex interactions .

Berwyn Zhang — Decomposer ( http://berwynzhang.com/2017/01/22/machine_learning/Factorization_Machines/ )
equation 9 Shows the second order FM What the model looks like :

among v Represents with each variable ( Users and projects ) dependent k Dimension potential vector , Bracket operators represent inner products . according to Steffen Rendle Original paper on Factoring machine , If we assume that each x(j) The vector is only in position u and i Non zero at , We will get the classical matrix decomposition model with deviation ( equation 3):

The main difference between these two equations is , Factorization machine introduces high-order interaction in terms of potential vectors , These potential vectors are also affected by classification or label data . This means that the model goes beyond co-occurrence , To find a stronger relationship between the potential representations of each feature .
Factorization Machines The loss function of the model is only the sum of the mean square error and the feature set , Like the equation 10 Shown :

import torch
from torch import nn
import torch.nn.functional as F
class MF(nn.Module):
def __call__(self, train_x):
# Pull out biases
biases = index_into(self.bias_feat.weight, train_x).squeeze().sum(dim=1)
# Initialize vector features using the feature weights
vector_features = index_into(self.feat.weight, train_x)
# Use factorization machines to pull out the interactions
interactions = factorization_machine(vector_features).squeeze().sum(dim=1)
# Final prediction is the sum of biases and interactions
prediction = biases + interactions
return prediction
def loss(self, prediction, target):
# Calculate the Mean Squared Error between target and prediction
loss_mse = F.mse_loss(prediction.squeeze(), target.squeeze())
# Compute L2 regularization over feature matrices
prior_feat = l2_regularize(self.feat.weight) * self.c_feat
# Add the MSE loss and feature regularization to get total loss
total = (loss_mse + prior_feat)
return total7、 ... and 、 Matrix decomposition of mixed flavors
The technology proposed so far implicitly regards user taste as unimodal —— That is, in a single potential vector . This may lead to a lack of nuance in representing users , under these circumstances , Dominant tastes may overwhelm more niche tastes . Besides , This may reduce the quality of the project presentation , So as to reduce belonging to multiple tastes / The separation of embedded spaces between project groups of type .
Maciej KulaMaciej Kula Propose and evaluate the representation of users as mixtures , If there are several different flavors , Represented by different taste vectors . Each taste vector is combined with an attention vector , Describes its ability to evaluate any given project . Then, user preferences are modeled as the weighted average of all user tastes , The weight is provided by the relevance of each flavor to the evaluation of a given item .
equation 11 The mathematical formula of this mixed taste model is given :

 It represents the user u Of m Flavor amxk matrix .
It represents the user u Of m Flavor amxk matrix . yes amxk matrix , Indicates from U_u The affinity of each flavor , Used to represent a specific item .
yes amxk matrix , Indicates from U_u The affinity of each flavor , Used to represent a specific item . yes soft-max Activation function .
yes soft-max Activation function . Give the mixing probability .
Give the mixing probability . Give the recommended score for each mixed ingredient .
Give the recommended score for each mixed ingredient .- Please note that , We assume that the constant variance matrix of all mixed components .
therefore , The following equation 12 The loss function is captured :

import torch
from torch import nn
import torch.nn.functional as F
class MF(nn.Module):
def __call__(self, train_x):
# These are the user and item indices
user_id = train_x[:, 0]
item_id = train_x[:, 1]
# Initialize a vector item using the item indices
vector_item = self.item(item_id)
# Pull out biases
bias_user = self.bias_user(user_id).squeeze()
bias_item = self.bias_item(item_id).squeeze()
biases = (self.bias + bias_user + bias_item)
# **NEW: Initialize the user taste & attention matrices using the user IDs
user_taste = self.user_taste[user_id]
user_attention = self.user_attention[user_id]
vector_itemx = vector_item.unsqueeze(2).expand_as(user_attention)
attention = F.softmax(user_attention * vector_itemx, dim=1)
attentionx = attention.sum(2).unsqueeze(2).expand_as(user_attention)
# Calculate the weighted preference to be the dot product of the user taste and attention
weighted_preference = (user_taste * attentionx).sum(2)
# This is a dot product of the weighted preference and vector item
dot = (weighted_preference * vector_item).sum(1)
# Final prediction is the sum of the biases and the dot product above
prediction = dot + biases
return prediction
def loss(self, prediction, target):
# Calculate the Mean Squared Error between target and prediction
loss_mse = F.mse_loss(prediction.squeeze(), target.squeeze())
# Compute L2 regularization over the biases for user and the biases for item matrices
prior_bias_user = l2_regularize(self.bias_user.weight) * self.c_bias
prior_bias_item = l2_regularize(self.bias_item.weight) * self.c_bias
# Compute L2 regularization over the user tastes and user attentions matrix
prior_taste = l2_regularize(self.user_taste) * self.c_vector
prior_attention = l2_regularize(self.user_attention) * self.c_vector
# Compute L2 regularization over item matrix
prior_item = l2_regularize(self.item.weight) * self.c_vector
# Add up the MSE loss + user & item biases regularization + item regularization + user taste & attention regularization
total = (loss_mse + prior_bias_item + prior_bias_user + prior_taste + prior_attention + prior_item)
return total8、 ... and 、 Variational matrix decomposition
The last variant of matrix factorization I want to introduce is called variational matrix factorization . Although most of the content discussed in blog articles so far is about the point estimation of optimization model parameters , But variation is about optimizing a posteriori , Roughly speaking , It expresses a series of model configurations consistent with the data .
The following are the actual reasons for the variation :
- Variational methods can provide alternative regularization .
- Variational methods can measure what your model doesn't know .
- Variational method can reveal implication and a novel method of grouping data .
We can make the equation 3 Matrix decomposition and variation in :(1) Replace the point estimation with the samples in the distribution , as well as (2) Replace the regularized point with the regularized new distribution . Mathematics is quite complicated . Wikipedia page about variable Bayesian method It's a guide to getting started . The most common variable Bayesian type is used Kullback-Leibler The divergence As a choice of dissimilar functions , This minimizes losses and is easy to handle .
import torch
from torch import nn
import torch.nn.functional as F
class MF(nn.Module):
def __call__(self, train_x):
# These are the user and item indices
user_id = train_x[:, 0]
item_id = train_x[:, 1]
# *NEW: Stochastically-sampled user & item vectors
vector_user = sample_gaussian(self.user_mu(user_id), self.user_lv(user_id))
vector_item = sample_gaussian(self.item_mu(item_id), self.item_lv(item_id))
# Pull out biases
bias_user = self.bias_user(user_id).squeeze()
bias_item = self.bias_item(item_id).squeeze()
biases = (self.bias + bias_user + bias_item)
# The user-item interaction is a dot product between the user and item vectors
ui_interaction = torch.sum(vector_user * vector_item, dim=1)
# Final prediction is the sum of the user-item interaction with the biases
prediction = ui_interaction + biases
return prediction
def loss(self, prediction, target):
# Calculate the Mean Squared Error between target and prediction
loss_mse = F.mse_loss(prediction.squeeze(), target.squeeze())
# Compute L2 regularization over the biases for user and the biases for item matrices
prior_bias_user = l2_regularize(self.bias_user.weight) * self.c_bias
prior_bias_item = l2_regularize(self.bias_item.weight) * self.c_bias
# *NEW: Compute the KL-Divergence loss over the Mu and Log-Variance for user and item matrices
user_kld = gaussian_kldiv(self.user_mu.weight, self.user_lv.weight) * self.c_kld
item_kld = gaussian_kldiv(self.item_mu.weight, self.item_lv.weight) * self.c_kld
# Add up the MSE loss + user & item biases regularization + user & item KL-Divergence loss
total = loss_mse + prior_bias_user + prior_bias_item + user_kld + item_kld
return totalNine 、 summary
Full code reference

- Variational matrix decomposition has the lowest training loss .
- The matrix decomposition with edge features has the lowest test loss .
- Factorization Machines The fastest training time .
边栏推荐
- JS password combination rule - 8-16 digit combination of numbers and characters, not pure numbers and pure English
- mysql_ Master slave synchronization_ Show slave status details
- Query the information of students whose grades are above 80
- Algorithmic interview questions
- Function of each layer of data warehouse
- 10. 509 Certificate (structure + principle)
- Learning Record V
- Banana pie bpi-m5 toss record (3) -- compile BSP
- Color space (2) -- YUV
- Enter an integer and a binary tree
猜你喜欢

JS foundation -- task queue and event loop

Calculation method of confusion matrix
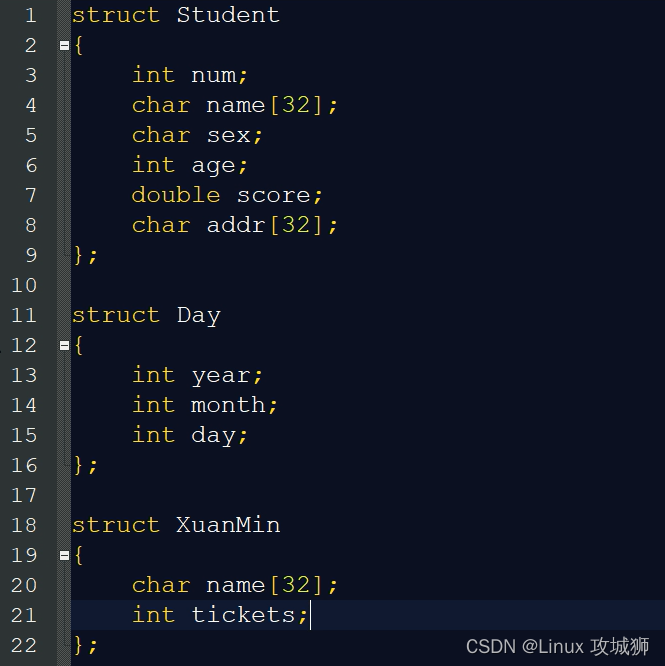
C language_ Structure introduction
Hal library serial port for note taking

Publish the project online and don't want to open a port
![[stm32f130rct6] idea and code of ultrasonic ranging module](/img/a6/1bae9d5d8628f00acf4738008a0a01.png)
[stm32f130rct6] idea and code of ultrasonic ranging module

Openlayers draw circles and ellipses

JS foundation -- hijacking of this keyword

Brief understanding of operational amplifier

kettle_ Configure database connection_ report errors
随机推荐
JS written test question -- prototype, new, this comprehensive question
Use and introduction of vim file editor
Introduction to Apache Doris grafana monitoring indicators
Win10 -- open the hosts file as an administrator
Resolve the error: org.apache.ibatis.binding.bindingexception
Can bus baud rate setting of stm32cubemx
Import and export using poi
List type to string type
Solve the error: could not find 'xxxtest‘
05 - MVVM model
Banana pie bpi-m5 toss record (3) -- compile BSP
Algorithmic interview questions
C language function operation
Mark down learning
How to use two stacks to simulate the implementation of a queue
Chrome process architecture
Concurrent programming day01
mysql_ Record the executed SQL
Merge sort / quick sort
ECMAScript new features
 Take the user factor as a function of time . On the other hand ,
Take the user factor as a function of time . On the other hand , remain unchanged , Because the project is static .
remain unchanged , Because the project is static . ) Make a career change .
) Make a career change . It represents the user u Of m Flavor amxk matrix .
It represents the user u Of m Flavor amxk matrix . yes amxk matrix , Indicates from U_u The affinity of each flavor , Used to represent a specific item .
yes amxk matrix , Indicates from U_u The affinity of each flavor , Used to represent a specific item . yes soft-max Activation function .
yes soft-max Activation function . Give the mixing probability .
Give the mixing probability . Give the recommended score for each mixed ingredient .
Give the recommended score for each mixed ingredient . https://github.com/khanhnamle1994/MetaRec/tree/master/Matrix-Factorization-Experiments
https://github.com/khanhnamle1994/MetaRec/tree/master/Matrix-Factorization-Experiments