DFS's complement to pruning

I mentioned pruning optimization earlier, one is the optimal solution pruning, the current path is not as good as the optimal solution, so it can be pruned, one is the optimal solutionIt is feasible pruning, that is, the current scheme is illegal, so it can also be pruned.

So here is a simple use of pruning optimization through the eight queens problem

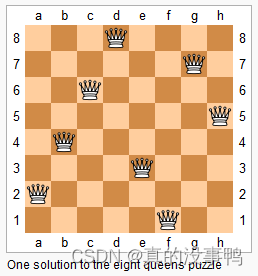
Classic Case - Eight Queens Problem

n−n−queens problem refers to placing nn queens on an n×nn×n chess board so that queens cannot attack each otherto, that is, no two queens can be on the same row, column, or slash.

Now, given an integer n, please output all the chess pieces that satisfy the conditions.

Input format

One line containing the integer n.

Output format

Each solution occupies n lines, and each line outputs a string of length n to represent the complete chessboard state.

Where . indicates that the square state of a certain position is empty, and Q indicates that a queen is placed on the square of a certain position.

After the output of each scheme is completed, a blank line is output.

Note: No extra spaces at the end of the line.

The order of the output schemes is arbitrary, as long as there are no repetitions and no omissions.

Data Range

1≤n≤9

Sample input:

4

Sample output:

.Q.....QQ.....Q...Q.Q......Q.Q..

Thoughts

Similar to searching for full arrangement, the search order can be the same as full arrangement, only one queen and only one queen can be placed in each row, so weYou can enumerate where each row of queens is placed like a full permutation.

Pay attention to pruning here. When we put the queen in a certain position, we need to judge whether there is a conflict. If there is a conflict, we don't need to go down.After the search is completed, the rest of the search does not need to be executed, and the process is pruned.In a nutshell, pruning means that it can be judged in advance that the current solution is illegal, so there is no need to search down.

How to judge whether there is a conflict? The title requires that each row, column and slash cannot be repeated, so use this conditionto prune.

Code implementation

#include using namespace std;int n;char p[20][20];bool lie[20],dg[20],udg[20];//lie indicates whether the column has been used, dg indicates a positive diagonal, and udg indicates an anti-diagonalvoid dfs(int u)//u represents the number of lines that have been drilled down at this time{if(u==n)//If u==n means that u has searched the last line, it can be output{for(int i=0;ib=y-x means subscript=u-i+n represents a positive diagonal, and because the subscript must be a positive number,So you can add a larger positive number, here we add n *///y=-x+b->b=y+x means subscript=u+i represents an antidiagonal{if(!lie[i]&&!dg[u+i]&&!udg[u-i+n])//lie indicates whether the column is used, dg[u+i] indicates whether a diagonal line is usedPass,//udg[u-i+n] indicates whether an anti-diagonal has been used{p[u][i]='Q';//If the queen can be filled at this time, let this point be Qlie[i]=dg[u+i]=udg[u-i+n]=1;dfs(u+1);lie[i]=dg[u+i]=udg[u-i+n]=0;//Restore the scenep[u][i]='.';}}}int main(){cin>>n;for(int i=0;i

If there are any mistakes or omissions, please correct me.