当前位置:网站首页>Postgraduate entrance examination | advanced mathematics Chapter4 indefinite integral
Postgraduate entrance examination | advanced mathematics Chapter4 indefinite integral
2022-07-23 21:34:00 【Caffiny】
One's deceased father grind | Advanced mathematics Chapter4 Indefinite integral
List of articles
I. Definition
- Primitive function — If F ′ ( x ) = f ( x ) , F ( x ) be called f ( x ) Primitive function F'(x)=f(x), F(x) be called f(x) Primitive function F′(x)=f(x),F(x) be called f(x) Primitive function
- Indefinite integral — set up F ( x ) by f ( x ) A primitive function of , F ( x ) + C be called f ( x ) The indefinite integral of F(x) by f(x) A primitive function of , F(x)+C be called f(x) The indefinite integral of F(x) by f(x) A primitive function of ,F(x)+C be called f(x) The indefinite integral of
- Notes:
- if f ( x ) ∃ ⇒ ∃ f(x) \exists\ \ \Rightarrow\exists f(x)∃ ⇒∃ Countless primitive functions
- The difference between any two primitive functions is a constant
- if f ( x ) continuity ⇒ ∃ f(x) continuity \ \ \Rightarrow\ \ \exists f(x) continuity ⇒ ∃ Primitive function
II. Indefinite integral tool
a. The basic formula
- ∫ k d x = k x + C \int k dx=kx+C ∫kdx=kx+C
- power function
- ∫ x a d x = 1 a + 1 x a + 1 + C ; ( a ≠ 1 ) \int x^a dx=\frac{1}{a+1}x^{a+1}+C;\quad (a \neq 1) ∫xadx=a+11xa+1+C;(a=1)
- ∫ 1 x d x = ln ∣ x ∣ + C \int \frac1x dx=\ln |x|+C ∫x1dx=ln∣x∣+C
- Exponential function
- ∫ a x d x = a x ln a + C ; ( a ≠ 1 ) \int a^x dx=\frac{a^x}{\ln a} + C;\quad (a \neq 1) ∫axdx=lnaax+C;(a=1)
- ∫ 1 x d x = x + C \int 1^x dx=x+C ∫1xdx=x+C
- Trigonometric functions
∫ sin x d x = − cos x + C \int \sin x dx = -\cos x + C ∫sinxdx=−cosx+C ∫ cos x d x = sin x + C \int \cos x dx = \sin x + C ∫cosxdx=sinx+C ∫ tan x d x = − ln ∣ cos x ∣ + C \int \tan x dx = -\ln |\cos x| + C ∫tanxdx=−ln∣cosx∣+C ∫ cot x d x = ln ∣ sin x ∣ + C \int \cot x dx = \ln |\sin x| + C ∫cotxdx=ln∣sinx∣+C ∫ sec x d x = ln ∣ sec x + tan x ∣ + C \int \sec x dx = \ln |\sec x + \tan x| + C ∫secxdx=ln∣secx+tanx∣+C ∫ csc x d x = ln ∣ csc x − cot x ∣ + C \int \csc x dx = \ln |\csc x-\cot x| + C ∫cscxdx=ln∣cscx−cotx∣+C ∫ sec 2 x d x = tan x + C \int \sec ^2x dx = \tan x + C ∫sec2xdx=tanx+C ∫ csc 2 x d x = − cot x + C \int \csc ^2x dx = -\cot x + C ∫csc2xdx=−cotx+C ∫ sec ( tan x ) d x = sec x + C \int \sec (\tan x) dx = \sec x + C ∫sec(tanx)dx=secx+C ∫ csc x cot x d x = − csc x + C \int \csc x\cot x dx = -\csc x + C ∫cscxcotxdx=−cscx+C - Square sum square difference
∫ 1 1 − x 2 d x = arcsin x + C \int \frac{1}{\sqrt{1-x^2}} dx = \arcsin x + C ∫1−x21dx=arcsinx+C ∫ 1 a 2 − x 2 d x = arcsin x a + C \int \frac{1}{\sqrt{a^2-x^2}} dx = \arcsin \frac xa + C ∫a2−x21dx=arcsinax+C ∫ 1 1 + x 2 d x = arctan x + C \int \frac1{1+x^2} dx = \arctan x + C ∫1+x21dx=arctanx+C ∫ 1 a 2 + x 2 d x = 1 a arctan x a + C \int \frac1{a^2+x^2} dx = \frac1a\arctan \frac xa + C ∫a2+x21dx=a1arctanax+C ∫ 1 x 2 + a 2 d x = ln ( x + x 2 + a 2 ) + C \int \frac1{\sqrt{x^2+a^2}} dx = \ln(x+\sqrt{x^2+a^2}) + C ∫x2+a21dx=ln(x+x2+a2)+C ∫ 1 x 2 − a 2 d x = ln ( x + x 2 − a 2 ) + C \int \frac1{\sqrt{x^2-a^2}} dx = \ln(x+\sqrt{x^2-a^2}) + C ∫x2−a21dx=ln(x+x2−a2)+C ∫ 1 x 2 − a 2 d x = 1 2 a ln ∣ x − a x + a ∣ + C \int \frac1{x^2-a^2} dx = \frac1{2a}\ln|\frac{x-a}{x+a}| + C ∫x2−a21dx=2a1ln∣x+ax−a∣+C ∫ a 2 − x d x = a 2 2 arcsin x a + x 2 a 2 − x 2 + C \int \sqrt{a^2-x} dx = \frac{a^2}{2}\arcsin\frac xa + \frac x2\sqrt{a^2-x^2} + C ∫a2−xdx=2a2arcsinax+2xa2−x2+C
b. Integral method
case1: The first kind of substitution integral method

case2: The second kind of transformation integral method
1. Irrational becomes rational

2. Triangular substitution , Square sum square difference
involves :
1. a 2 − x 2 ⇒ x = a sin t ⇒ a cos t \sqrt{a^2-x^2}\quad\Rightarrow\quad x=a\sin t \quad\Rightarrow\quad a\cos t a2−x2⇒x=asint⇒acost
2. a 2 + x 2 ⇒ x = a tan t ⇒ a sec t \sqrt{a^2+x^2}\quad\Rightarrow\quad x=a\tan t \quad\Rightarrow\quad a\sec t a2+x2⇒x=atant⇒asect
3. x 2 − a 2 ⇒ x = a sec t ⇒ a tan t \sqrt{x^2-a^2}\quad\Rightarrow\quad x=a\sec t \quad\Rightarrow\quad a\tan t x2−a2⇒x=asect⇒atant
3. Integration by parts
( u v ) ′ = u ′ v + u v ′ ∫ ( u v ) ′ d x = ∫ u ′ v d x + ∫ u v ′ d x u v = ∫ v d u + ∫ u d v ∫ u d v = u v − ∫ v d u \begin{aligned} (uv)'&=u'v+uv' \\ \int (uv)' dx &= \int u'v dx + \int uv'dx \\ uv &= \int v du + \int u dv \\ \int u dv &= uv - \int v du \end{aligned} (uv)′∫(uv)′dxuv∫udv=u′v+uv′=∫u′vdx+∫uv′dx=∫vdu+∫udv=uv−∫vdu
∫ power ∗ finger d x \int power * finger dx ∫ power ∗ finger dx, Left power function

∫ power ∗ logarithm d x \int power * logarithm dx ∫ power ∗ logarithm dx, Retention logarithm

∫ power ∗ Triangle d x \int power * Triangle dx ∫ power ∗ Triangle dx
Notes:- Trigonometric functions sin cos \sin\cos sincos It must be once

- If you encounter sin 2 cos 2 \sin^2\cos^2 sin2cos2 Reduce the degree with half angle formula
sin ( 2 x ) = 2 sin x cos x cos ( 2 x ) = cos 2 x + sin 2 x \sin(2x)=2\sin x\cos x \\\cos(2x)=\cos^2 x + \sin^2 x sin(2x)=2sinxcosxcos(2x)=cos2x+sin2x
- If you encounter tan cot sec cot \tan\cot\sec\cot tancotseccot Wait for an even number of times

- Trigonometric functions sin cos \sin\cos sincos It must be once
∫ power ∗ Anti triangle d x \int power * Anti triangle dx ∫ power ∗ Anti triangle dx, Leave inverse trigonometric function


∫ e a x ∗ sin b x \int e^{ax}*\sin bx ∫eax∗sinbx or ∫ e a x ∗ cos b x \int e^{ax}*\cos bx ∫eax∗cosbx, Leave trigonometric function

∫ sec n x d x \int \sec^nx dx ∫secnxdx or ∫ csc n x d x \int \csc^n xdx ∫cscnxdx, among n n n It's odd
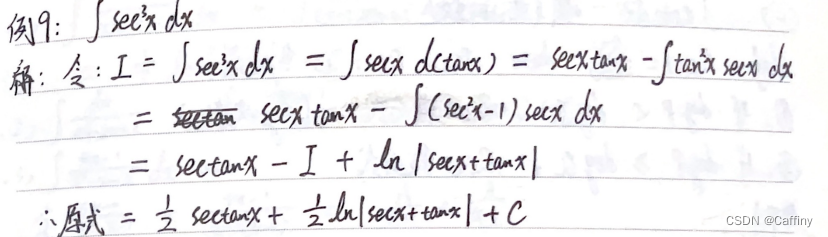
∫ sec n x d x \int \sec^nx dx ∫secnxdx or ∫ csc n x d x \int \csc^n xdx ∫cscnxdx, among n n n For the even
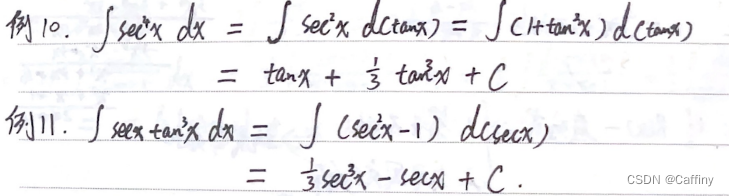
III. Indefinite integral of special function
a. Rational functions
Definition : Integrand function R ( x ) R(x) R(x) Is a rational function , among R ( x ) = P ( x ) Q ( x ) R(x)=\frac{P(x)}{Q(x)} R(x)=Q(x)P(x), among P ( x ) Q ( x ) P(x)Q(x) P(x)Q(x) They are polynomials
When P ( x ) Maximum number of times < Q ( x ) Maximum number of times P(x) Maximum number of times < Q(x) Maximum number of times P(x) Maximum number of times <Q(x) Maximum number of times , R ( x ) R(x) R(x) Is the true fraction
When P ( x ) Maximum number of times ≥ Q ( x ) Maximum number of times P(x) Maximum number of times \geq Q(x) Maximum number of times P(x) Maximum number of times ≥Q(x) Maximum number of times , R ( x ) R(x) R(x) Is a false fraction
case1: False fraction
Ideas : take False fraction Turn into polynomial + True fraction 
case2: True fraction
Ideas : 1. Molecules do not move ; 2. Denominator factorization into partial sums 

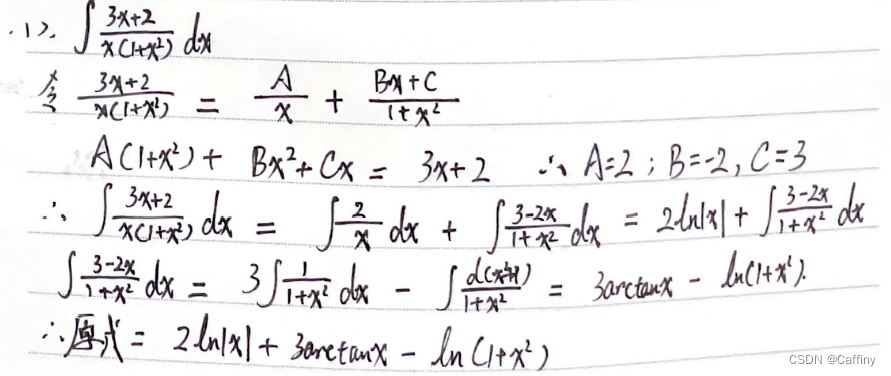
b. Irrational function


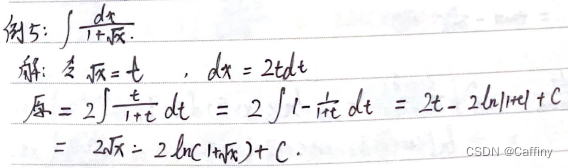
c. Indefinite integral of trigonometric rational function

边栏推荐
- At 12 o'clock on July 23, 2022, the deviation from the top of the line of love life hour appeared, maintaining a downward trend and waiting for the rebound signal.
- Openlayers instances advanced mapbox vector tiles advanced mapbox vector maps
- Deep learning - NLP classic papers, courses, papers and other resources sorting and sharing
- Cmake learning
- 221. Largest square ● &1277. Square submatrix with statistics all 1 ● ●
- 宇树A1机器狗手势控制
- Basic knowledge of mobile phone testing
- 集群聊天服务器:如何解决跨服务器通信问题 | redis发布-订阅
- WinDbg practice -- Introduction
- Problems and abuse of protocol buffers
猜你喜欢

& 9 nodemon automatic restart tool

Connect with Hunan Ca and use U_ Key login

Typescript Basics

The total ranking of blogs is 918

&9 nodemon自动重启工具
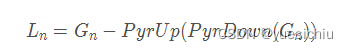
Opencv image processing Laplace pyramid

Openlayers instances advanced mapbox vector tiles advanced mapbox vector maps

Synchro esp32c3 Hardware Configuration Information serial port Print Output

One of QT desktop whiteboard tools (to solve the problem of unsmooth curve -- Bezier curve)

Openlayers instance advanced view positioning advanced view positioning
随机推荐
集群聊天服务器:工程目录的创建
2022-7-23 12点 程序爱生活 小时线顶背离出现,保持下跌趋势,等待反弹信号出现。
Failed to introspect class feignclientfactorybean exception troubleshooting
[arXiv] notes on uploading papers for the first time
[complex overloaded operator]
Proof of green Tao theorem (1): preparation, notation and Gowers norm
Looking for the missing class name
First acquaintance with JS (programming suitable for beginners)
Flink principle and development summary (detailed)
Cluster chat server: network module chatServer
221. Largest square ● &1277. Square submatrix with statistics all 1 ● ●
How to use cesium knockout?
CMake的学习
Cluster chat server: Design of database table
Several methods of obtaining longitude and latitude by cesium
Identify some positions in the parenthesis sequence
NLP field history most complete must read classic papers classification, sorting and sharing (with Chinese analysis)
Scala programming (elementary)
Mysql database index
prime_ series_ level-1