当前位置:网站首页>PAT B1063
PAT B1063
2022-06-25 19:57:00 【Madness makes freedom】
1063 Calculate the spectral radius (20 branch )
In mathematics , Matrix “ Spectral radius ” Is the supremum of the modular set of its eigenvalues . In other words , For a given n Eigenvalues of a complex space { a1+b1i,⋯,an+bni }, Their modules are the square of the sum of squares of real and imaginary parts , and “ Spectral radius ” Is the maximum module .
Now let's give some eigenvalues of complex space , Please calculate and output the spectral radius of these eigenvalues .
Input format :
Enter the first line to give a positive integer N(≤ 10 000) Is the number of input eigenvalues . And then N That's ok , Each line gives 1 The real and imaginary parts of eigenvalues , Separated by spaces . Be careful : The problem is to ensure that both the real part and the imaginary part are absolute values that do not exceed 1000 The integer of .
Output format :
Output the spectral radius in one line , Round to decimal 2 position .
sample input :
5
0 1
2 0
-1 0
3 3
0 -3
sample output :
4.24The topic is clearly understood , It should be done by lifting the key , But unfortunately , The definition of spectral radius is not clear to me . It's hard !!
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
int main()
{
int n,a,b,sum_squ=0;
cin >> n;
while(n--)
{
cin >> a >> b;
sum_squ=max(sum_squ,a*a+b*b);
}
double sqr=sqrt(sum_squ*1.0);
printf("%.2f\n",sqr);
return 0;
}
边栏推荐
- Est - il sûr d'ouvrir un compte avec de nouvelles dettes? Une faible Commission est - elle crédible?
- Case: count the most characters and times
- MySQL view explanation
- Apifox simple understanding -- the integrator of web side testing
- Jsonp non homologous interaction (click trigger)
- Mysql database design suggestions
- Process of vacuum and vacuum full
- 在打新债开户证券安全吗
- Redis cache preheating & avalanche & breakdown & penetration
- Automatic fitting when the applet reaches the top
猜你喜欢

LNMP compilation and installation

Laravel validation rule followed Role of auth:: id()
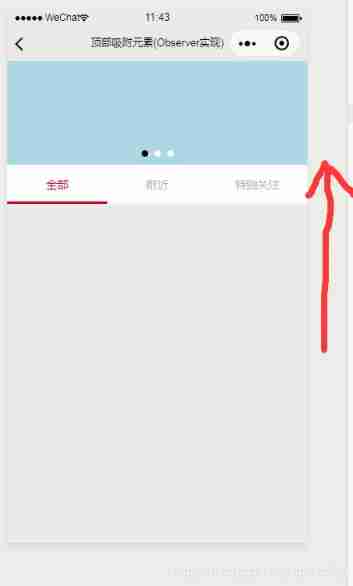
Automatic fitting when the applet reaches the top

Arduino read temperature

Lilda Bluetooth air conditioning receiver helps create a more comfortable road life

Ali visual AI training camp -day05- creativity day - your image recognition project

Jsonp processing non homologous

Determine whether it is a web page opened on wechat

2020-12-09 laravel . Env file loading mechanism process

Ali vision AI training camp-day01
随机推荐
Some pictures of real machine preview development and debugging are not shown
Wechat applet swiper simple local picture display appears large blank
Process of vacuum and vacuum full
Vulnhub range the planes:earth
Number of wechat applet custom input boxes
Applet canvas generate sharing Poster
PostgreSQL division considerations
wooyun-2014-065513
Idea common plug-ins
Is CICC wealth safe? How long does it take to open an account
Jsonp function encapsulation
Wechat applet connects to the server to display mqtt data information
Can the stock account opened through qiniu school be used? Is the fund safe?
System optimization method
Network security detection and prevention test questions (V)
Determine whether it is a web page opened on wechat
Ali visual AI training camp -day03- construction of electronic photo album (face and expression recognition)
ECS 7-day practical training camp (Advanced route) -- day01 -- setting up FTP service based on ECS
Yum command
在打新債開戶證券安全嗎?低傭金靠譜嗎