当前位置:网站首页>20200802 T3 I always like [generating function exclusion, Lagrangian inversion]
20200802 T3 I always like [generating function exclusion, Lagrangian inversion]
2022-06-11 07:30:00 【Master. Yi】
Title Description
Yes n n n Stones of different colors , Each of these c i c_i ci individual , Remember that the length of the extremely long continuous segment of a stone sequence after its head and tail are connected is l i l_i li, Find the sequence of all stones 1 ∏ l i ! \frac 1{\prod l_i!} ∏li!1 And .
n ≤ 1 0 5 , ∑ c i ≤ 2 ∗ 1 0 5 n\le10^5,\sum c_i\le2*10^5 n≤105,∑ci≤2∗105
Topic analysis
First, consider how to remove the connection between the head and the tail .
Because it limits the length , It's easy to think of dividing each color into several sections , Then merge , But it is not good to ensure that the same colors are not combined .
Let's not talk about tolerance and exclusion , Problem solving gives a method to solve the problem by generating function :
The weight of an extremely long continuous segment is 1 l e n ! \frac 1{len!} len!1
We are going to divide each color into many segments and then combine them . Consider giving a weight to each length segment a i a_i ai, So that for a length of l e n len len In all divisions of the extremely long color segment ∏ a i \prod a_i ∏ai The sum of is equal to 1 l e n ! \frac 1{len!} len!1, namely :
set up F = ∑ a i x i , G = e x − 1 F=\sum a_ix^i,G=e^x-1 F=∑aixi,G=ex−1
So there are F + F 2 + F 3 . . . = F 1 − F = G F+F^2+F^3...=\frac F{1-F}=G F+F2+F3...=1−FF=G
thus F = G G + 1 = e x − 1 e x F=\frac G{G+1}=\frac {e^x-1}{e^x} F=G+1G=exex−1
So the question becomes : Divide each color into segments , Then arrange all the segments of different colors together , The color of adjacent segments can be the same after arrangement , The length is i i i The weight of the segment of is a i a_i ai, The weight of the whole sequence is the product of each segment , Find the sum of sequence weights of all schemes .
So we just need to find the division of each color into i i i Sum of weights of segments , Then different paragraphs use EGF Just multiply it .
and m m m The stones are divided into i i i The sum of the weights of the segments is g i = [ x m ] F i g_i=[x^m]F^i gi=[xm]Fi
Then consider adding the condition that the head meets the tail , Put... On the ring 1 The number point is marked , It is equivalent to that there will now be color segments spanning N N N and 1 1 1, If we follow the sequence method, we will miss the contribution of these schemes , Consider cyclic shifts , Put across N N N and 1 1 1 The color segment of moves back in sequence , Until the dividing point between it and the previous paragraph is N ] [ 1 N~][~1 N ][ 1, Then such a scheme only corresponds to the scheme on a sequence .
So you just need to multiply the weight of the first paragraph by an additional length , We can calculate the contribution across the ring .
So for a person who has m m m The color of a stone , When its first segment is the first segment of the whole sequence , It points i i i The sum of the contributions of the paragraph should be :
g i = [ x m ] F i − 1 x F ′ = [ x m − 1 ] ( F i ) ′ ∗ 1 i = [ x m ] F i ∗ m i g_i=[x^m]F^{i-1}xF'\\=[x^{m-1}](F^i)'*\frac 1i\\ =[x^m]F^i*\frac mi gi=[xm]Fi−1xF′=[xm−1](Fi)′∗i1=[xm]Fi∗im
Find out g i g_i gi Get the corresponding two EGF, Then divide and conquer NTT Merger then .
and i ∈ [ 1 , n ] , [ x n ] F i i\in[1,n],[x^n]F^i i∈[1,n],[xn]Fi Find out F F F The compound inverse of can be calculated by extended Lagrangian inversion , The specific measures are written in This blog .
and F F F The compound inverse of H H H Satisfy e H − 1 e H = x {e^H-1\over e^H}=x eHeH−1=x, namely e H = 1 1 − x e^H=\frac 1{1-x} eH=1−x1, therefore H = ln 1 1 − x = ∑ i ≥ 1 1 i x i H=\ln {\frac 1{1-x}}=\sum_{i\ge 1}\frac 1ix^i H=ln1−x1=∑i≥1i1xi
Code:
#include<bits/stdc++.h>
#define maxn 550005
#define rep(i,j,k) for(int i=(j),LIM=(k);i<=LIM;i++)
#define per(i,j,k) for(int i=(j),LIM=(k);i>=LIM;i--)
using namespace std;
void output(vector<int>&a){
rep(i,0,a.size()-1) printf("%d ",a[i]); puts("");
}
const int mod = 998244353;
int w[maxn],r[maxn],WL,lg[maxn],fac[maxn],inv[maxn],invf[maxn];
int Pow(int a,int b){
int s=1;for(;b;b>>=1,a=1ll*a*a%mod) b&1&&(s=1ll*s*a%mod);return s;}
void init(int n){
WL=1; while(WL<=n) WL<<=1;
w[WL>>1]=1; int wn=Pow(3,(mod-1)/WL);
for(int i=WL/2+1;i<WL;i++) w[i]=1ll*w[i-1]*wn%mod;
for(int i=WL/2-1;i>=1;i--) w[i]=w[i<<1];
fac[0]=fac[1]=inv[0]=inv[1]=invf[0]=invf[1]=1;
rep(i,2,WL-1) fac[i]=1ll*fac[i-1]*i%mod,inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod,invf[i]=1ll*invf[i-1]*inv[i]%mod,lg[i]=lg[i>>1]+1;
}
int upd(int x){
return x+(x>>31&mod);}
void NTT(int *a,int len,int flg){
if(flg^1) reverse(a+1,a+len);
for(int i=0;i<len;i++) if(i<(r[i]=r[i>>1]>>1|(i&1?len>>1:0))) swap(a[i],a[r[i]]);
for(int i=2,l=1,v;i<=len;l=i,i<<=1)
for(int j=0;j<len;j+=i)
for(int k=j,o=l;k<j+l;k++,o++)
a[k+l]=upd(a[k]-(v=1ll*w[o]*a[k+l]%mod)),a[k]=upd(a[k]+v-mod);
if(flg^1) for(int i=0,Inv=mod-(mod-1)/len;i<len;i++) a[i]=1ll*a[i]*Inv%mod;
}
typedef vector<int> Poly;
Poly operator * (const Poly &A,const Poly &B){
static int a[maxn],b[maxn]; int n=A.size(),m=B.size(),L=1<<(lg[n+m-2]+1);
if(n<=20||m<=20||n+m<=200) {
rep(i,0,n+m-2) a[i]=0; rep(i,0,n-1) rep(j,0,m-1) a[i+j]=(a[i+j]+1ll*A[i]*B[j])%mod;}
else{
rep(i,0,L-1) a[i]=i<n?A[i]:0,b[i]=i<m?B[i]:0;
NTT(a,L,1),NTT(b,L,1);
rep(i,0,L-1) a[i]=1ll*a[i]*b[i]%mod;
NTT(a,L,-1);
}
return Poly(a,a+n+m-1);
}
Poly operator + (Poly A,const Poly &B){
if(B.size()>A.size()) A.resize(B.size());
rep(i,0,A.size()-1) A[i]=upd(A[i]+B[i]-mod);
return A;
}
Poly INV(const Poly &A,int n){
static int B[maxn],a[maxn]; B[B[1]=0]=Pow(A[0],mod-2);
for(int k=2,L=4;k<n<<1;k=L,L<<=1){
memcpy(a,&A[0],min(n,k)<<2); rep(i,k,L-1) a[i]=B[i]=0;
NTT(a,L,1),NTT(B,L,1); rep(i,0,L-1) B[i]=1ll*B[i]*upd(2-1ll*a[i]*B[i]%mod)%mod; NTT(B,L,-1);
memset(B+k,0,k<<2);
}
return Poly(B,B+n);
}
Poly LN(const Poly &A,int n){
Poly a(n-1),b(INV(A,n));
rep(i,0,n-2) a[i]=1ll*A[i+1]*(i+1)%mod;
a=a*b,b[0]=0;
rep(i,1,n-1) b[i]=1ll*a[i-1]*inv[i]%mod;
return b;
}
Poly EXP(const Poly &A,int n){
Poly B{
1},b;
for(int k=2,L=4;k<n<<1;k=L,L<<=1){
B.resize(k),b=LN(B,k); rep(i,0,min(n,k)-1) b[i]=upd((i==0)-b[i]+A[i]);
B=B*b,B.resize(min(n,k));
}
return B;
}
Poly L;
void calc(Poly &g1,Poly &g2,int n){
g1.resize(n+1),g2.resize(n+1);
Poly A(L.begin(),L.begin()+n);
rep(i,0,n-1) A[i]=1ll*A[i]*(mod-n)%mod;
A=EXP(A,n);
rep(i,1,n) g2[i]=1ll*A[n-i]*invf[i-1]%mod,g1[i]=1ll*A[n-i]*invf[i-1]%mod*inv[n]%mod;
}
Poly g1[maxn],g2[maxn];
void solve(int l,int r){
if(l==r) return;
int mid=(l+r)>>1;
solve(l,mid),solve(mid+1,r);
Poly A(g1[l]*g1[mid+1]),B(g1[l]*g2[mid+1]+g2[l]*g1[mid+1]);
g1[l].swap(A),g2[l].swap(B);
}
int n,c[maxn],Mx,Sum;
int main()
{
freopen("always.in","r",stdin);
freopen("always.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&c[i]),Mx=max(Mx,c[i]),Sum+=c[i];
init(max(2*Mx,Sum));
L=LN(Poly(inv+1,inv+Mx+1),Mx);
for(int i=1;i<=n;i++) calc(g1[i],g2[i],c[i]);
solve(1,n);
int ans=0;
rep(i,n,g2[1].size()-1) ans=(ans+1ll*g2[1][i]*fac[i-1])%mod;
printf("%d\n",ans);
}
here It is an inclusive approach , The general idea is to calculate the inclusion exclusion coefficient by how many times each segment number is calculated , However, the color of the last section and the second section shall be different from that of the first section , The above approach does not need to consider this problem .
边栏推荐
- Typora set markdown syntax inline mode
- 2、 User login and registration
- 【Oracle 数据库】奶妈式教程day02 数据库管理工具SQLPLUS的使用
- 正则表达式匹配
- Building a full-featured NAS server with raspberry pie (05): playing with video and audio & sorting out movies
- 2022低压电工操作证考试题模拟考试平台操作
- Outer margin collapse
- Matrix tree theorem
- P1390 sum of common divisors (Mobius inversion)
- 【POJ3691】DNA repair (AC自动机+DP)
猜你喜欢

Modular notes

Directrix of ellipse
![[STL source code analysis] summary notes (12): functors and adapters](/img/6d/a3a9cde2c8792579af7505c2226914.jpg)
[STL source code analysis] summary notes (12): functors and adapters

Sdl-2 thread logic

2、 User login and registration

JVM Learning record (7) - - class Loading Process and parent delegation Model
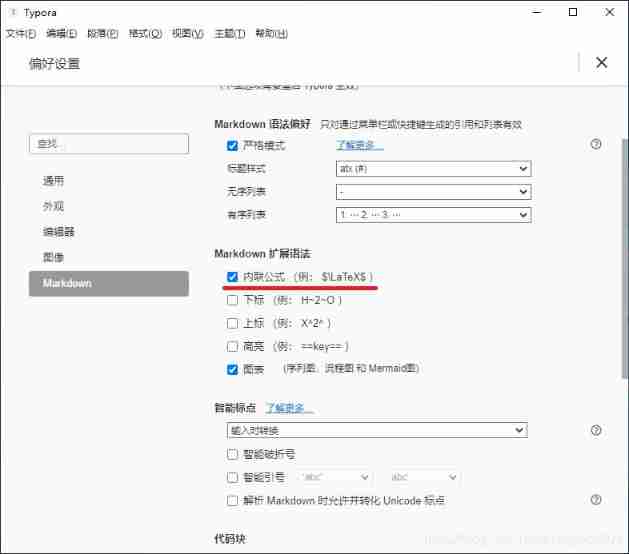
Typora set markdown syntax inline mode

Miscellany C language
QObject usage skills -- control function class

QT table display data
随机推荐
MySQL设置管理员密码无法生效的案例一则
CRMEB/V4.4标准版打通版商城源码小程序公众号H5+App商城源码
Qstring to hexadecimal qstring
Sdl-3 YUV playback
nosqlzoo刷题-1
Compound RateModel合約解析
SQLZOO刷题记录-3
Pat class A by category
一、SQLServer2008安裝(帶密碼)、創建數據庫、C#窗體項目測試
群晖DS918创建m.2 固态硬盘SSD读写缓存
Set center alignment
R language Parallel Computing practice tutorial
如果要存 IP 地址,用什么数据类型比较好?99%人都会答错!
Post-processing of ffmpeg miscellaneous notes
2022.5.30-6.5 AI行业周刊(第100期):三年时光
Niuke wrong question 3.1
Mobile console Gobang (first draft of detailed design)
Android和iOS逆向分析/安全检测/渗透测试框架
C+tinycthread implementation thread
[Oracle database] mammy tutorial day03 Sorting Query