【1.2.投资的收益和风险】

模型的建立与求解

多目标规划问题通过一定形式的改变可以化为单目标的线性规划。
$$max\sum _{i=0}^n(r_i-p_i)x_i,$$
$$s.t.\{\begin{array}{ll}\frac{q_i{x}_i}{M}\le a& i=1,2,\cdots ,n,\\ {\sum }_{i=0}^n(1+p_i)x_i=M& x_i\ge 0，i=1,2,\cdots ,n。\end{array}$$
由于matlab中只能使用min，所以在敲代码的时候需要把数学模型中的max改编成min.
$$minf=[-0.05,-0.27,-0.19,-0.185,-0.185]\cdot [x_0,x_1,x_2,x_3,x_4{]}^T$$
$$s.t.\{\begin{array}{l}{x}_0+1.01x_1+1.02x_2+1.045x_3+1.065x_4=1\\ 0.025x_1\le a\\ 0.015x_2\le a\\ 0.055x_3\le a\\ 0.026x_4\le a\\ x_i\ge 0,i=0,1,\cdots ,4\end{array}$$
由于a是任意给定的风险度，不同的投资者有不同的分享度，下面从a=0开始，以步长0.001进行循环搜索，由此可以使用MATLAB进行编程。

clc,clear
a=0;
hold on
while a<0.05
    c=[-0.05,-0.27,-0.19,-0.185,-0.185];
    A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])];
    b=a*ones(4,1);
    Aeq=[1,1.01,1.02,1.045,1.065];
    beq=1;
    LB=zeros(5,1);
    [x,q]=linprog(c,A,b,Aeq,beq,LB);
    q=-q;
    plot(a,q,'*k');
    a=a+0.001;
end
xlabel('风险度变化a'),ylabel('总体收益Q')

综合分析，应该选择曲线的转折点作为最优投资组合，a=0.006, Q=0.20.
然后我们需要求出来每个项目需要投多少钱，就需要各个x求出来。
于是下面进行编程。

clc,clear
a=0.006;
    c=[-0.05,-0.27,-0.19,-0.185,-0.185];
    A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])];
    b=a*ones(4,1);
    Aeq=[1,1.01,1.02,1.045,1.065];
    beq=1;
    LB=zeros(5,1);
    [x,q]=linprog(c,A,b,Aeq,beq,LB)
    q=-q

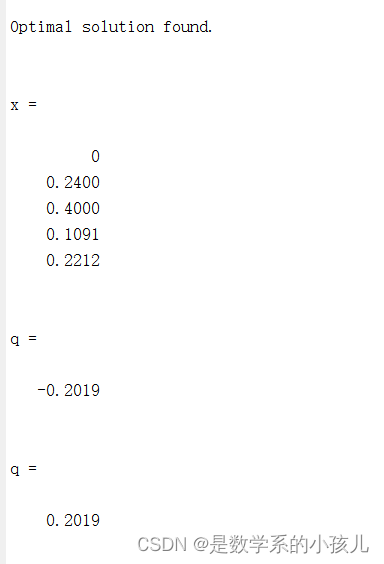
到这里给出总的金额的话，就可以具体根据比例关系求得每个项目需要投资的最优金额了。