Matlab simulation of depth information extraction and target ranging based on binocular camera images

Catalog

1. Algorithm description

2. Partial procedure

3. Preview of some simulation drawings

4. Source code acquisition method

---

1. Algorithm description

        Binocular cameras are generally composed of two horizontally placed cameras, the left eye and the right eye . Of course, it can also be made into two items , But the mainstream binoculars we see are made of left and right . In the left and right binocular cameras , We can think of both cameras as pinhole cameras . They are placed horizontally , It means that the aperture centers of both cameras are located in x On the shaft . Their distance is called the baseline of the binocular camera （Baseline, Write it down as b）, Is an important parameter of binocular . Binocular cameras are generally composed of two horizontally placed cameras, the left eye and the right eye . Of course, it can also be made into two items , But the mainstream binoculars we see are made of left and right . In the left and right binocular cameras , We can think of both cameras as pinhole cameras . They are placed horizontally , It means that the aperture centers of both cameras are located in x On the shaft . Their distance is called the baseline of the binocular camera （Baseline, Write it down as b）, Is an important parameter of binocular .

        Consider a space point P, It looks alike in the left eye and the right eye , Write it down as PL,PR. Due to the existence of camera baseline , The two imaging positions are different . Ideally , Because the left and right cameras are only in x There is displacement on the shaft , therefore P Your image is only in x Axis （ Corresponding to the image u Axis ） There are differences . We remember its coordinates on the left as uL, The right coordinate is uR. that , Their geometric relationship is shown in the figure 1 On the right . According to the triangle P−PL−PR and P−OL−OR Similarity relation of , Yes ：       

Put it in order ：

here d Is the difference between the abscissa of the left and right graphs , It's called parallax （Disparity）. According to parallax , We can estimate the distance between a pixel and the camera . Parallax is inversely proportional to distance ： The greater the parallax , The closer you get . meanwhile , Because the parallax is at least one pixel , So there is a theoretical maximum of binocular depth , from fb determine . We see , When the baseline is longer , The maximum distance that can be measured by your eyes will become farther ; conversely , Small binocular devices can only measure very close distances .

2. Partial procedure

% Calculate the depth distance of the object 
PL=imread('IMAGES\p1.jpg');
subplot(241),imshow(PL),title(' Image taken on the left ');
PL=rgb2gray(PL);
PL=255-PL;
PL1=im2bw(PL,0.8);
subplot(242),imshow(PL1),title(' Threshold segmentation image ');
se1=strel('rectangle',[5 5]);
PL2=imclose(PL1,se1);   % Closed operation 
se2=strel('rectangle',[5 5]);
PL3=imopen(PL2,se2);   % Open operation 
subplot(243),imshow(PL2),title(' Morphological processing ');
imwrite(PL3,'PL3.bmp','bmp')
k=1;sum1=0;
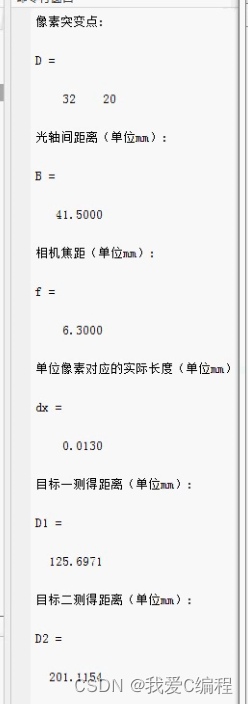
for j=1:518        % Calculate the pixel mutation point of target one 
    for i=1:388
        sum1=sum1+PL3(i,j);
        
    end
    k=k+1;
    P(k)=sum1/318;
    sum1=0;
end
x=1:518;
y=P(x);
subplot(244),plot(x,y),title(' Gray scale change diagram ');
plot(x,y);
for i=2:518        % Calculate the pixel mutation point of target 2 
    if ((P(i-1)<0.01)&(P(i)>0.01)&(P(i)<0.16))
        Z(1)=i;
        continue
    end
    if ((P(i-1)<0.1)&(P(i)>0.16))
        Z(2)=i;
        continue
    end
end
%===============================
 % Calculate the target position of the image on the right 
%===============================
PR=imread('IMAGES\p2.jpg');
subplot(245),imshow(PR);title(' Take an image on the right ');
PR=rgb2gray(PR);
PR=255-PR;
PR1=im2bw(PR,0.8);
subplot(246),imshow(PR1);title(' Threshold segmentation image ');
se1=strel('rectangle',[5 5]);
PR2=imclose(PR1,se1); 
se2=strel('rectangle',[5 5]);
PR3=imopen(PR2,se2); 
subplot(247),imshow(PR3),title(' Morphological processing ');
k=1;sum2=0;
for j=1:518
    for i=1:388
        sum2=sum2+PR3(i,j);
        
    end
    k=k+1;
    Q(k)=sum2/318;
    sum2=0;
end

3. Preview of some simulation drawings

 

4. Source code acquisition method

Click the download link ：

Depth information extraction and target ranging based on binocular camera images matlab Simulation + Program operation video

Access method 2：

Blog resource item , Search for resources with the same name as blog .

Access method 3：

If the download link fails , Blogger wechat contact .

A_059