当前位置:网站首页>tag单调栈-单调栈预备知识-lt.739. 每日温度
tag单调栈-单调栈预备知识-lt.739. 每日温度
2022-08-03 04:55:00 【菜菜的大数据开发之路】
lt.739. 每日温度
[案例需求]

[思路分析一, 双重for循环遍历]
/** * 最简单莫过于双重循环,笔试时至少不会丢分 * 时间复杂度:O(n^2) * 空间复杂度:O(n) */
//外层循环是一次遍历给定数组, 内层循环是不断的寻找比外层循环此时遍历到的元素大的数,
//并用res持续的记录下最大的index差值
public int[] dailyTemperatures(int[] T) {
int[] res = new int[T.length];
for (int i = 0; i < T.length - 1; i++) {
for (int j = i + 1; j < T.length; j++) {
if (T[j] > T[i]) {
res[i] = j - i;
break;
}
}
}
return res;
}
[思路分析二, 单调栈简单原理]
通常是
一维数组, 要寻找一个元素的右边或者左边第一个比自己大或者小的元素的位置, 此时我们就可以想到用单调栈。
- 本题就是找到一个元素右边第一个比自己大的元素, 所以可以用单调栈。
那么单调栈的原理是什么呢?为什么时间复杂度是O(n)就可以找到每一个元素的右边第一个比它大的元素位置呢?
单调栈的本质是
空间换时间, 因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素, 优点是只需要遍历一次。
[单调栈的使用]
- 使用单调栈首先明确:
- 单调栈里存放的元素是什么?
单调栈里只需要存放元素的下标i就可以了,如果需要使用对应的元素,直接T[i]就可以获取。
- 单调栈里元素是递增还是递减的?
从栈顶到栈底的顺序
- 本题, 我们要使用递增循序(再强调一下是指从栈顶到栈底的顺序),因为只有递增的时候,往栈中加入一个元素i,才知道栈顶元素在数组中右面第一个比栈顶元素大的元素是i (curreentIndex, 即当前for循环遍历到的数的索引为i)。
[具体思路 + 代码实现]
- 维护一个存储下标的单调栈, 从栈底到栈顶的下标对应的温度列表中的温度依次递减, 如果一个下标在单调栈中, 则表示尚未找到下一次温度更高的下标。
- 正向遍历温度列表, 对于温度列表中的每个元素 T[i], 如果栈为空, 则直接将i进栈, 如果栈不为空, 则比较栈顶元素preIndex对应温度T[preIndex]和当前温度T[i], 如果T[i] > T[preIndex], 则将preInndex移除, 并将preIndex对应的天数赋为i - preIndex, 重复上述操作, 直到栈为空, 或者栈顶元素对应的温度小于等于当前温度, 然后将i出栈.
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
//维护递减栈,后入栈的元素总比栈顶元素小。
//比对当前元素与栈顶元素的大小
//若当前元素 < 栈顶元素:入栈
/若当前元素 > 栈顶元素:弹出栈顶元素,记录两者下标差值即为所求天数
//这里用栈记录的是 T 的下标。
Deque<Integer> stack = new LinkedList<>();
int len = temperatures.length;
int[] res = new int[len];
int index = 0;
for(int i = 0; i < len; i++){
int temperature = temperatures[i];
//当前元素 > 栈顶index的元素
//弹出preIndex, 记录preIndex与当前元素i的index差值, 更新到res[preIndex]
while(!stack.isEmpty() && temperature > temperatures[stack.peek()]){
int preIndex = stack.pop();
System.out.println("i为: " + preIndex);
//System.out.println("preIndex为: " + preIndex);
res[preIndex] = i - preIndex;
System.out.println(Arrays.toString(res));
}
//当前元素 <= 栈顶index的元素
//入栈当前元素
stack.push(i);
}
return res;
}
}

边栏推荐
- 7.Keras开发简介
- 社交电商如何做粉丝运营?云平台怎么选择商业模式?
- 常见荧光染料修饰多种基团及其激发和发射波长数据一览数据
- 索引创建、删除与使用
- rosbag工具plotjuggler无法打开rosbag的问题
- [Harmony OS] [ARK UI] ETS context basic operations
- Where is the value of testers
- mysql 创建索引的三种方式
- Concepts and Methods of Exploratory Testing
- [Harmony OS] [ArkUI] ets development graphics and animation drawing
猜你喜欢
随机推荐
Fluorescent marker peptides FITC/AMC/FAM/Rhodamine TAMRA/Cy3 / Cy5 / Cy7 - Peptide
How to use the interface management tool YApi?Beautiful, easy to manage, super easy to use
typescript40-class类的保护修饰符
2022暑假牛客多校联赛第一场
Get the Ip tool class
Record some bugs encountered - when mapstruct and lombok are used at the same time, the problem of data loss when converting entity classes
redis键值出现 xacxedx00x05tx00&的解决方法
自组织是管理者和成员的双向奔赴
【Harmony OS】【ArkUI】ets开发 图形与动画绘制
接口和协议
typescript39-class类的可见修饰符
技术分享 | 接口自动化测试中如何对xml 格式做断言验证?
测试人员的价值体现在哪里
Practical application of WebSocket
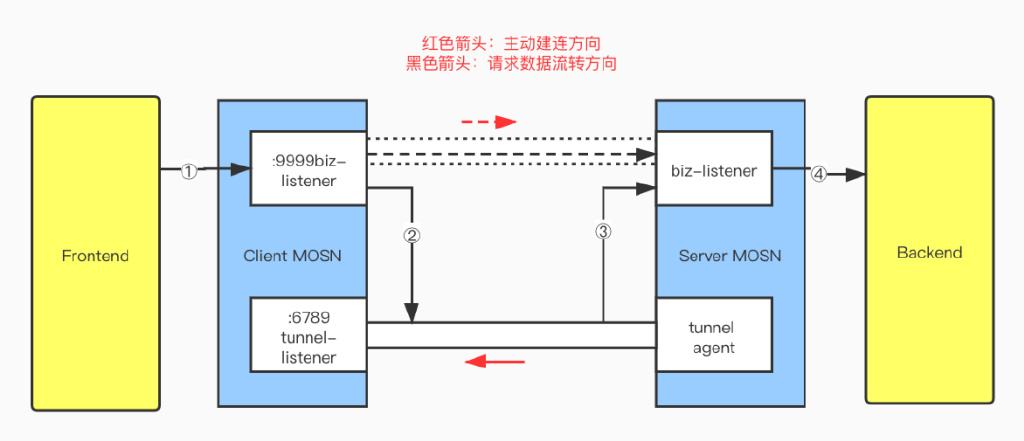
Detailed explanation of MOSN reverse channel
Peptides mediated PEG DSPE of phospholipids, targeted functional materials - PEG - RGD/TAT/NGR/APRPG
js的垃圾回收机制
【Harmony OS】【ARK UI】Date 基本操作
UV decomposition of biotin - PEG2 - azide | CAS: 1192802-98-4 biotin connectors
好消息!北京、珠海PMP考试时间来啦