DFS对剪枝的补充

前面说过剪枝优化，一个是最优解剪枝，当前的路径不如最优解，这样就可以剪枝，一个是可行性剪枝，就是当前这个方案不合法，这样也可以剪枝。

所以这里通过八皇后问题来简单运用一下剪枝优化

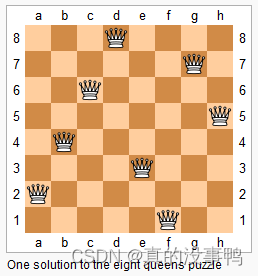
经典案例-八皇后问题

n−n−皇后问题是指将 nn 个皇后放在 n×nn×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

 现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数 n。

输出格式

每个解决方案占 n 行，每行输出一个长度为 n 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。

注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

1≤n≤9

输入样例：

4

输出样例：

.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

思路

        类似于搜索全排列，搜索顺序可以像全排列一样，每一行只能放一个皇后而且只能放一个皇后，所以我们可以像全排列一样枚举每一行皇后放在什么位置。

        这里要注意剪枝，当我们把皇后放在某个位置时要判断是否有冲突，如果有冲突的话就不用往下搜了，这样剩下的搜索就不用执行了，这个过程就交剪枝。剪枝简单来说就是可以提前判断当前这个方案是不合法的，就没必要往下搜了，下面的子树就没用了，删掉直接回溯，这个过程就交剪枝。

        这个怎么判断是否有冲突呢，题目要求每一行每一列和每一斜线上不能有重复放，那么就用这个条件来剪枝。

代码实现

#include <iostream>
using namespace std;
int n;
char p[20][20];
bool lie[20],dg[20],udg[20];//lie表示列是否用过,dg表示某条正对角线，udg表示某条反对角线 
void dfs(int u)//u代表此时已经深入到第几行了 
{
    if(u==n)//如果u==n代表u已经搜索完最后一行 ，可以输出了 
    {
        for(int i=0;i<n;i++)
        cout<<p[i]<<endl;
        cout<<endl;
      return;
    }
    for(int i=0;i<n;i++)
	//i表示列数，每次搜索第u行时从第一列开始搜，满足条件继续下一行的 
    //搜索，如果不满足条件则跳过继续搜索 
    //下面的dg[u+i]和udg[u+i]不太好理解
	//u表示行数，i表示列数，u可以看成y，i看成x。根据判断某直线是否用过可以用截距判断。所以由
	/*y=x+b->b=y-x即下标=u-i+n  表示某条正对角线，又因为表示下标必须是正数，
	所以可以加上一个较大的正数，这里我们加上n */
	//y=-x+b->b=y+x即下标=u+i  表示某条反对角线 
    {
        if(!lie[i]&&!dg[u+i]&&!udg[u-i+n])//lie表示列是否用过，dg[u+i]表示某条正对角线是否用过，
		//udg[u-i+n]表示某条反对角线是否用过 
        {
            p[u][i]='Q';//如果此时可以填皇后，令此点为Q 
            lie[i]=dg[u+i]=udg[u-i+n]=1;
            dfs(u+1);
            lie[i]=dg[u+i]=udg[u-i+n]=0;//恢复现场 
            p[u][i]='.';
        }
    }
}
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
    {
    	for(int j=0;j<n;j++)
    	p[i][j]='.';
	}
    dfs(0);
    return 0;
}

如有错漏之处，敬请指正。