当前位置:网站首页>单调栈一些题目练习
单调栈一些题目练习
2022-08-04 10:55:00 【minato_yukina】
最近发现单调栈不怎么会熟练使用,写点东西提醒下自己
第一题
给你一个数组 a i a_i ai,问你对于一个长度为 i i i的连续区间,最大化该区间的最小值。你需要回答长度1~n的区间的答案并且输出他们。
对于这个问题,其实我已经遇过好几次了,这类问题需要关注的是谁作为最小值而造成的区间影响.
我们认为 a i ai ai就是当前区间的最小值,那么我们需要处理出当前该元素的最左边索引 l l l,最右索引 r r r,那么它就可以作为答案算入区间 r − l + 1 中 r-l+1中 r−l+1中.
对于处理出 l , r l,r l,r这两个值,这就是单调栈的作用了。
首先处理r数组,从前往后扫,如果碰到一个值 a i ai ai大于栈顶元素,取出栈顶所有元素,把他们的值 r [ j ] = i r[j]=i r[j]=i
再处理 l l l数组,从后边往前边扫,如果碰到一个元素大于当前 i i i,和 r r r一样的处理
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
const int INF = 1e9+7;
typedef long long ll;
typedef pair<int,int> pii;
#define all(a) (a).begin(), (a).end()
#define pb(a) push_back(a)
vector<int> G[maxn];
int a[maxn];int s[maxn];
int l[maxn],r[maxn],ans[maxn];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
int top = 0;
for(int i=1;i<=n;i++){
while(top>0&&a[s[top]]>a[i]){
r[s[top]] =i-1;top--;
}
top++;
s[top] = i;
}
while(top>0) r[s[top]] = n,top--;
for(int i=n;i>=1;i--){
while(top>0&&a[s[top]]>a[i]){
l[s[top]] = i+1;top--;
}
top++;s[top]=i;
}
while(top>0) l[s[top]]=1,top--;
for(int i=1;i<=n;i++){
int len = r[i]-l[i]+1;
ans[len] = max(ans[len],a[i]);
}
// for(int i=1;i<=n;i++){
// cout<<i<<" "<<l[i]<<" "<<r[i]<<"\n";
// }
for(int i=n-1;i>=1;i--){
ans[i] = max(ans[i+1],ans[i]);
}
for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
}
第二题
与上题类似地,使用单调栈来分别处理第i个牛是否有那样的点x,
x . h > 2 ∗ a i . h , a b s ( x . x − a i . x ) < = d x.h>2*a_i.h,abs(x.x-a_i.x)<=d x.h>2∗ai.h,abs(x.x−ai.x)<=d.
我们使用一个单调队列维护队列中的h元素单调下降性,当前元素的 h h h大于队尾元素时,不断地弹出队尾.
当距离不满足要求时,不断弹出队首,这样剩下的元素就是最可能合法地与i匹配的牛,这个元素显然就是队首,因为它的h元素值最大,而且位置也符合要求,其他元素不可能比它更适合.
对于左边的情况我们正序扫描一遍,右边的情况倒序扫描一遍即可.
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
const int INF = 1e9+7;
typedef long long ll;
typedef pair<int,int> pii;
#define all(a) (a).begin(), (a).end()
#define pb(a) push_back(a)
vector<int> G[maxn];
struct Node{
int x,h;
bool operator <(const Node&rhs)const{
return x<rhs.x;
}
}a[maxn];
int que[maxn];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n,d;cin>>n>>d;
for(int i=1;i<=n;i++) cin>>a[i].x>>a[i].h;
sort(a+1,a+1+n);
deque<int> dq;
vector<bool> left(n+1,false),right(n+1,false);
for(int i=1;i<=n;i++){
while(!dq.empty()&&a[dq.back()].h<a[i].h) dq.pop_back();
while(!dq.empty()&&abs(a[i].x-a[dq.front()].x)>d) dq.pop_front();
if(!dq.empty()&&a[dq.front()].h>=2*a[i].h) left[i] = true;
dq.push_back(i);
}
while(!dq.empty()) dq.pop_front();
for(int i=n;i>=1;i--){
while(!dq.empty()&&a[dq.back()].h<a[i].h) dq.pop_back();
while(!dq.empty()&&abs(a[i].x-a[dq.front()].x)>d) dq.pop_front();
if(!dq.empty()&&a[dq.front()].h>=2*a[i].h) right[i] = true;
dq.push_back(i);
}
// for(int i=1;i<=n;i++){
// cout<<a[i].x<<" "<<a[i].h<<" ";
// }
// cout<<"\n";
// for(int i=1;i<=n;i++) cout<<left[i]<<" ";
// cout<<"\n";
// for(int i=1;i<=n;i++) cout<<right[i]<<" ";
// cout<<"\n";
int ans=0;
for(int i=1;i<=n;i++){
if(left[i]&&right[i]) ans++;
}
cout<<ans<<"\n";
}
第三题
仍然是一个比较明显的单调队列,如果我们断环为链,发现不成立的标准就是对于一个位置 i i i,有 s u m j − s u m i < 0 ( j > = i & & j < = i + n − 1 ) sum_j-sum_i<0(j>=i\&\&j<=i+n-1) sumj−sumi<0(j>=i&&j<=i+n−1).那么我们发现只要选取区间 [ i + 1 , i + n − 1 ] 中的最小的 s u m j 即可 , 使用单调队列维护这段最小值就能算出答案 [i+1,i+n-1]中的最小的sum_j即可,使用单调队列维护这段最小值就能算出答案 [i+1,i+n−1]中的最小的sumj即可,使用单调队列维护这段最小值就能算出答案.
#include<bits/stdc++.h>
using namespace std;
const int maxn = 2e6+5;
const int INF = 1e9+7;
typedef long long ll;
typedef pair<int,int> pii;
#define all(a) (a).begin(), (a).end()
#define pb(a) push_back(a)
vector<int> G[maxn];ll a[maxn],sum[maxn];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++) a[i+n] = a[i];
for(int i=1;i<=2*n;i++) sum[i] = sum[i-1]+a[i];
deque<int> dq;ll ans = 0;
for(int i=2*n;i>=1;i--){
while(!dq.empty()&&dq.front()-i>n) dq.pop_front();
if(i<=n&&!dq.empty()&&sum[dq.front()]-sum[i]>=0) ans++;
while(!dq.empty()&&sum[dq.front()]>=sum[i]) dq.pop_back();
dq.push_back(i);
}
cout<<ans<<"\n";
}
边栏推荐
- What is the principle of thermal imaging temperature measurement?Do you know?
- tp5+微信小程序 分片上传
- zabbix部署
- BOSS 直聘回应女大学生连遭两次性骚扰:高度重视求职者安全,可通过 App 等举报
- There are 12 balls, including 11 weight, only one, don't know is light or heavy. Three times in balance scales, find out the ball.
- 浅析深度学习在图像处理中的应用趋势及常见技巧
- MATLAB程序设计与应用 3.1 特殊矩阵
- MySQL之my.cnf配置文件
- 有12个球,其中11个重量相等,只有1个不一样,不知是轻还是重.用天平秤三次,找出这个球.
- CompletableFuture接口核心方法介绍
猜你喜欢
Advanced transcriptome analysis and R data visualization hot registration (2022.10)
Graphical Hands-on Tutorial--ESP32 OTA Over-the-Air Upgrade (VSCODE+IDF)
C语言*小白的探险历程

8月活动|51CTO十七周年庆,发博文得茶具/笔记本/T恤等礼品!
【Idea series】idea configuration

利用pytest hook函数实现自动化测试结果推送企业微信
JUC (1) threads and processes, concurrency and parallelism, thread state, locks, producers and consumers
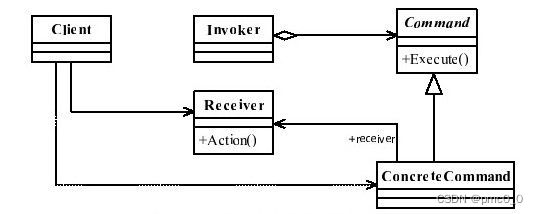
命令模式(Command)

热成像测温的原理是什么呢?你知道吗?

《迁移学习导论》第2版,升级内容抢先看!
随机推荐
Graphic and text hands-on tutorial--ESP32 MQTT docking EMQX local server (VSCODE+ESP-IDF)
Heap Sort
zabbix部署
Four ways to traverse a Map
热成像测温的原理是什么呢?你知道吗?
Small program containers accelerate the construction of an integrated online government service platform
Introduction to the core methods of the CompletableFuture interface
bitset的基本用法
cubemx stm32 afm3000 module gas flow sensor driver code
vscode插件设置——Golang开发环境配置
什么是终端特权管理
MySQL 45 讲 | 11 怎么给字符串字段加索引?
在 .NET MAUI 中如何更好地自定义控件
C#/VB.NET:在 Word 中设置文本对齐方式
Jenkins使用手册(1) —— 软件安装
解析treeSet集合进行自定义类的排序
自己实现一个枚举validation校验器
Graphical Hands-on Tutorial--ESP32 One-Key Network Configuration (Smartconfig, Airkiss)
tp5+微信小程序 分片上传
【LeetCode】98.验证二叉搜索树