当前位置:网站首页>22牛客多校1 J.Serval and Essay (启发式合并)
22牛客多校1 J.Serval and Essay (启发式合并)
2022-08-01 07:25:00 【樱落二瓣七里香】
大致题意 : 一个n个点m条边的无重边无自环的有向图, 初始均为白点, 若某个点的前驱节点均为黑点, 则该点可以被染黑, 初始可任意染黑一点, 求最大化图中黑点的数量
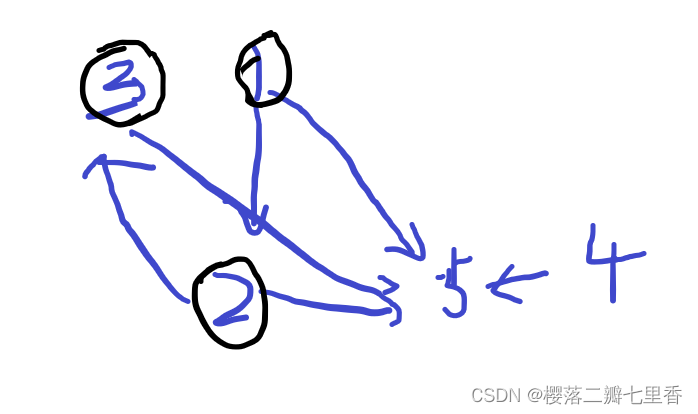
思路 : 首先可以画一张图, 如样例, 起始我们染黑1, 后续2, 3可被染黑, 不难发现, 1,2,3可以互相影响, 染黑3 不如 染黑2, 染黑2 不如 染黑 1, 这时我们可以将这三个点看做一个点, 即进行合并, 可以发现合并后并不会对原图产生影响, 如节点 5 在合并和 由{1, 2, 3} 和 {4} 控制并不能染黑, 若有另一点能到{1, 2, 3}, 则{1, 2, 3}并不能合并, 可知合并后的{1, 2, 3}的前后节点不受影响, 即当前合并后的节点集合的节点数即为最大, 若有多个集合取极大值即可
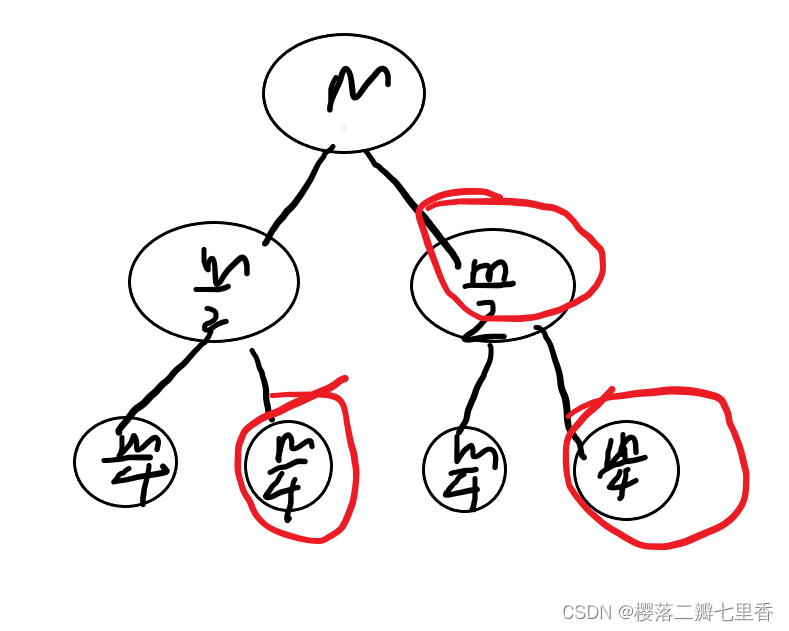
显然暴力是会超时的, 因为会遍历到所有重边来进行合并, 这里可以想到用启发式合并来进行操作, 对于两个可以连接的集合, 我们只遍历出边数小的那个集合, 将它与出边大的合并, 来优化时间复杂度, 最坏情况下m条边, 分为m/2, m/2两个集合, 每次只遍历一个, 不断向下合并, 复杂度为 O(m/2 * log m), 再加上需要用到set操作, 总时间复杂度为O(m/2 * log m * log m), 是可以做的
代码如下:
#include <bits/stdc++.h>
using namespace std;
stringstream ss;
#define endl "\n"
typedef long long ll;
typedef pair<int, int> PII;
const int N = 2e5+10, M = 30, mod = 1e9+7;
const int INF = 0x3f3f3f3f;
int n;
int p[N], sz[N]; // p为并查集集合, sz为集合大小
set<int> pre[N], ne[N]; // 分别记录前驱节点和后缀节点
int find(int x)
{
if(x != p[x]) p[x] = find(p[x]);
return p[x];
}
void merge(int x, int y) // 启发式合并
{
x = find(x), y = find(y);
if(x == y) return;
if(ne[x].size() < ne[y].size()) swap(x, y); // 保证x是出边大的那个
p[y] = x, sz[x] += sz[y]; // 将y向x合并
vector<PII> seg; // 合并一边x,y后, 对于{x, y}和其他点 可能还能继续合并, 用seg保存起来, dfs合并
for(auto t : ne[y])
{
pre[t].insert(x), ne[x].insert(t), pre[t].erase(y); // 合并操作
if(pre[t].size() == 1) seg.push_back({t, x});
}
for(auto t : seg) merge(t.first, t.second); // 继续合并
}
void solve(int t)
{
cin>>n;
for(int i = 1; i<=n; i++) p[i] = i, sz[i] = 1, pre[i].clear(), ne[i].clear();
for(int i = 1; i<=n; i++)
{
int k;
cin>>k;
for(int j = 1; j<=k; j++)
{
int x;
cin>>x;
ne[x].insert(i);
pre[i].insert(x);
}
}
for(int i = 1; i<=n; i++)
{
if(pre[i].size() == 1) merge(*pre[i].begin(), i); // 对入边为1的点与当前点进行合并
}
int res = 0;
for(int i = 1; i<=n; i++) res = max(res, sz[i]);
cout<<"Case #"<<t<<": "<<res<<endl;
}
int main()
{
ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
// solve();
int T;
cin>>T;
for(int i = 1; i<=T; i++)
{
solve(i);
}
}
边栏推荐
- Information system project managers must recite the work of the core test site (56) Configuration Control Board (CCB)
- 问下 mysql向pg同步多个表的话 有什么好的方案吗?
- LabVIEW RT中的用户界面更新速度
- Bean的生命周期
- 信息系统项目管理师必背核心考点(五十六)配置控制委员会(CCB)的工作
- 监听父元素宽高,自适应插件大小
- LeetCode240+312+394
- pytest接口自动化测试框架 | parametrize源码解析
- Monitor the width and height of the parent element, adapt to the size of the plug-in
- Srping bean in the life cycle
猜你喜欢
Three aspects of Ali: How to solve the problem of MQ message loss, duplication and backlog?

我说过无数遍了:从来没有一种技术是为灵活组合这个目标而设计的

mysql中添加字段的相关问题

配置我的kitty

Fist game copyright-free music download, League of Legends copyright-free music, can be used for video creation, live broadcast

MVVM项目开发(商品管理系统一)
LabVIEW RT中的用户界面更新速度

LabVIEW中局部变量和全局变量的分配
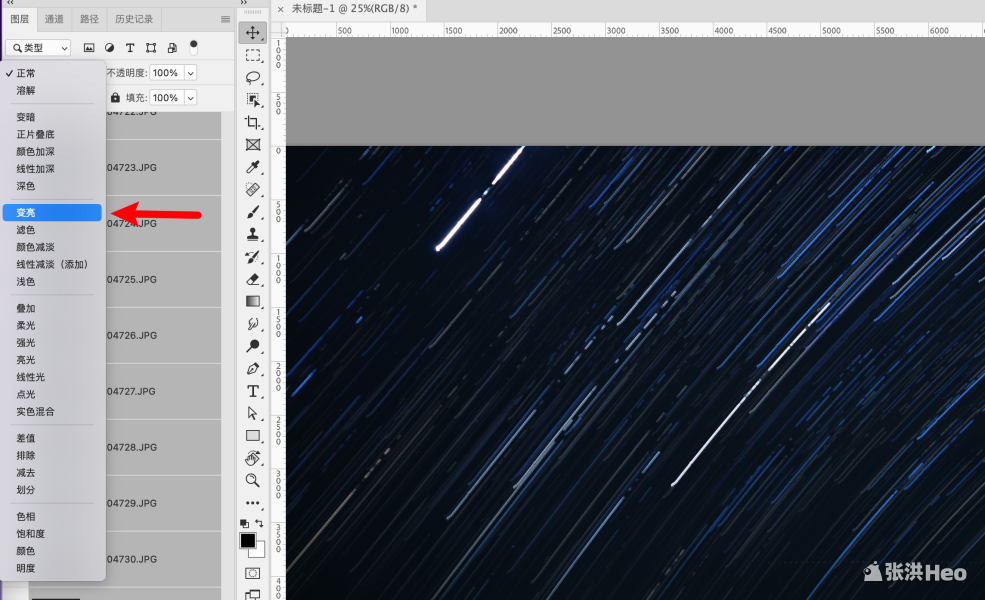
如何使用Photoshop合成星轨照片,夜空星轨照片后期处理方法

仿牛客网项目总结
随机推荐
图片无损压缩软件哪个好用:试试完全免费的JPG-C 图片批量修整压缩减肥工具吧 | 最新jpg批量修整工具下载
仿牛客网项目总结
Explosive 30,000 words, the hardest core丨Mysql knowledge system, complete collection of commands [recommended collection]
Srping bean in the life cycle
实战演练 Navicat 中英文模式切换
app 自动化 通过工具查看app 元素 (三)
【ASWC Arxml结构分解】-7-Explicit(显式)和Implicit(隐式) Sender-Receiver communication描述差异
响应式织梦模板园林花卉类网站
信息系统项目管理师必背核心考点(五十六)配置控制委员会(CCB)的工作
特别数的和
Dbeaver connect the MySQL database and error Connection refusedconnect processing
VSCode 快捷键及通用插件推荐
数据机构----线性表之单向链表
Image lossless compression software which works: try completely free JPG - C image batch finishing compression reduces weight tools | latest JPG batch dressing tools download
Datagrip error "The specified database userpassword combination is rejected..."Solutions
05-SDRAM:仲裁
R语言使用tidyquant包的tq_transmute函数计算持有某只股票的天、月、周收益率、ggplot2使用条形图可视化股票月收益率数据、使用百分比显示Y轴坐标数据、使用不同的色彩表征正负收益率
自制一款远程控制软件——VeryControl
Upgrade to heavyweight lock, lock reentrancy will lead to lock release?
Practical training Navicat Chinese and English mode switching