当前位置:网站首页>自控原理学习笔记-系统稳定性分析(1)-BIBO稳定及Routh判据
自控原理学习笔记-系统稳定性分析(1)-BIBO稳定及Routh判据
2022-07-27 16:22:00 【Miracle Fan】
自控原理学习笔记
自控原理学习笔记专栏
文章目录
1.输入输出稳定-对于CLTIS
1.1两种稳定状态
1.1.1 BIBO稳定
定义:如果一个系统在一个有界输入或扰动作用下其响应是有限的。
充要条件:
y ( t ) = ∫ 0 t g ( τ ) u ( t − τ ) d τ ⇒ ∣ y ( t ) ∣ ≤ ∫ 0 t ∣ g ( τ ) ∣ ⋅ ∣ u ( t − τ ) ∣ d τ ≤ M ∫ 0 t ∣ g ( τ ) ∣ d τ y(t)=\int_0^tg(\tau)u(t-\tau)d\tau\Rightarrow |y(t)|\le \int _0^t|g(\tau)|\cdot |u(t-\tau)|d\tau \le M\int_0^t|g(\tau)|d\tau y(t)=∫0tg(τ)u(t−τ)dτ⇒∣y(t)∣≤∫0t∣g(τ)∣⋅∣u(t−τ)∣dτ≤M∫0t∣g(τ)∣dτ
若要使y(t)有界,则充要条件为 ∣ g ( τ ) ∣ |g(\tau)| ∣g(τ)∣绝对可积不可积例子: g ( t ) = 1 t − 1 g(t)=\frac{1}{t-1} g(t)=t−11
对于CLTIS,满足BIBO则只有左半平面极点:
假设传递函数是冲激响应的Laplace变换,于是:
G ( s ) = ∫ 0 ∞ g ( t ) e − s t d t ⇒ ∣ G ( s ) ∣ ≤ ∫ 0 ∞ ∣ g ( t ) ∣ ⋅ ∣ e − s t ∣ d t = ∫ 0 ∞ ∣ g ( t ) ∣ ⋅ ∣ e − σ t ∣ d t * i f σ ≥ 0 , ∣ G ( s ) ∣ ∣ s = σ + i w → ∞ ≤ ∫ 0 ∞ ∣ g ( t ) ∣ ⋅ ∣ e − σ t ∣ d t ≤ ∫ 0 ∞ ∣ g ( t ) ∣ d t G(s)=\int_0^\infty g(t)e^{-st}dt\Rightarrow|G(s)|\le\int_0^\infty |g(t)|\cdot|e^{-st}|dt=\int_0^\infty|g(t)|\cdot|e^{-\sigma t}|dt\\ \Longrightarrow if \quad\sigma \ge 0,\quad |G(s)||_{s=\sigma+iw}\rightarrow\infty\le\int^\infty_0|g(t)|\cdot|e^{-\sigma t}|dt\le\int_0^\infty|g(t)|dt G(s)=∫0∞g(t)e−stdt⇒∣G(s)∣≤∫0∞∣g(t)∣⋅∣e−st∣dt=∫0∞∣g(t)∣⋅∣e−σt∣dt*ifσ≥0,∣G(s)∣∣s=σ+iw→∞≤∫0∞∣g(t)∣⋅∣e−σt∣dt≤∫0∞∣g(t)∣dt
∣ g ( t ) ∣ |g(t)| ∣g(t)∣无界,与BIBO稳定矛盾,所有只有当 σ < 0 \sigma<0 σ<0,满足条件。
1.1.2 零输入稳定(渐近稳定)
- 定义:当t趋近于无穷,由初始条件产生的响应趋于0。
- 稳定充分必要条件:
- 对于 ∀ s i , R e ( s i ) < 0 时 , C L T I S 渐 近 稳 定 \forall s_i,Re(s_i)<0时,CLTIS渐近稳定 ∀si,Re(si)<0时,CLTIS渐近稳定
- R e ( s i ) > 0 ∣ ∣ 有重虚根 , C L T I S 不 稳 定 Re(s_i)>0||\text{有重虚根},CLTIS不稳定 Re(si)>0∣∣有重虚根,CLTIS不稳定
- 仅存在单重虚根,其他 R e ( s j ) < 0 Re(s_j)<0 Re(sj)<0,LTIS临界定界。
- 相关例子:
1.1.3 稳定性相关说明
- 对于LTIS,BIBO、零输入稳定都要求特征值均位于复平面左边
- 对于LTIS,稳定性只取决于系统固有性质(特征值),与外界条件无关。
- 稳定性具有一个局部特性(多个稳定点),但只在时变系统和非线性系统体现,时不变系统是全局的。
2. Routh-Hurwitz判据
2.1 CLTIS稳定的必要条件
系统特征方程所有系数大于0
2.2 Routh判据
列些Routh表
s n a n a n − 2 a n − 4 … s^n\quad a_n \quad a_{n-2}\quad a_{n-4} \quad \dots snanan−2an−4…
s n − 1 a n − 1 a n − 3 a n − 5 … s^{n-1}\quad a_{n-1} \quad a_{n-3}\quad a_{n-5} \quad \dots sn−1an−1an−3an−5…
s n − 2 b 1 b 2 b 3 … s^{n-2}\quad b_1 \quad b_2\quad b_3 \dots sn−2b1b2b3…
s n − 3 c 1 c 2 … s^{n-3}\quad c_1 \quad c_2\quad \dots sn−3c1c2…
…………
s 0 h 1 s^0 \quad h_1 s0h1
常规计算
b 1 = − [ a n a n − 2 a n − 1 a n − 3 ] a n − 1 b 2 = − [ a n a n − 4 a n − 1 a n − 5 ] a n − 1 c 1 = − [ a n − 1 a n − 3 b 1 b 2 ] b 1 c 2 = − [ a n − 1 a n − 5 b 1 b 3 ] b 1 b_1=-\frac{ \begin{bmatrix} a_{n}& a_{n-2} \\ a_{n-1}& a_{n-3} \end{bmatrix} } {a_{n-1}} \quad b_2=-\frac{ \begin{bmatrix} a_{n}& a_{n-4} \\ a_{n-1}& a_{n-5} \end{bmatrix} } {a_{n-1}}\\ c_1=-\frac{ \begin{bmatrix} a_{n-1}& a_{n-3} \\ b_1&b_2 \end{bmatrix} } {b_1} \quad c_2=-\frac{ \begin{bmatrix} a_{n-1}& a_{n-5} \\ b_1&b_3 \end{bmatrix} } {b_1} b1=−an−1[anan−1an−2an−3]b2=−an−1[anan−1an−4an−5]c1=−b1[an−1b1an−3b2]c2=−b1[an−1b1an−5b3]判断稳定方法:
第一列系数符号改变次数,就是特征根位于右半s平面的个数
稳定充要条件:表中第一列系数全大于0
2.3 相关应用
(1)首列系数为0
利用小 ϵ \epsilon ϵ法代替零值项,按常规方法继续求解。
若第一列全为正数,系统也不是渐近稳定,而是存在纯虚根,临界稳定
(2)某行系数全为0
表明s平面有对称于原点的实根,或共轭虚根
- 取全为0的前一行,以其系数为辅助方程(只取偶次)
- 对辅助方程求导,系数代替全为0行
- 继续常规步骤
- 解辅助方程得到对称根
(3)相关稳定性问题
利用换元的思想。
如求实部均小于2,则设u=s+2代入方程,将u当作方程变量,进行求解。
2.4 Hurwitz判据
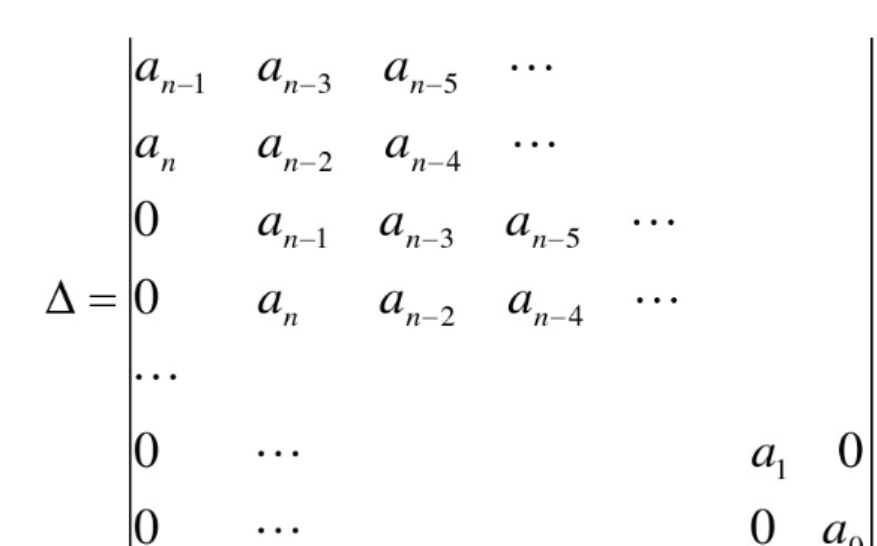
判据:各阶主子式大于0
=s+2代入方程,将u当作方程变量,进行求解。
2.4 Hurwitz判据
[外链图片转存中…(img-JIuo2Ql8-1648098107527)]
判据:各阶主子式大于0
边栏推荐
猜你喜欢
随机推荐
Hbuilder submission code
Interceptor interceptor
WPS turns off annoying advertisements
Whole body multifunctional massage instrument chip-dltap602sd
idea 2020.1社区版下载体验
Nodejs 模板引擎ejs
商品推荐和分类商品推荐
Aircraft collision detection
LED带风扇护眼学习台灯触摸芯片-DLT8S12A
怎样产生标准分布或高斯分布的随机数
How to send external mail to the company mailbox server on the Intranet
C basic concepts list description suggestions collection
Bathroom with demister vanity mirror touch chip-dlt8t10s
Day 3 of leetcode question brushing
Extension of ES6 value
Collection of software design suggestions of "high cohesion and low coupling"
WSN Journal indexed by SCI(转)
飞机大战碰撞检测
TypeError: conv2d(): argument ‘padding‘ (position 5) must be tuple of ints, not str【报错】
Music rhythm colorful gradient lamp chip -- dlt8s04a- Jericho