[ARC092D] Two Faced Edges

[ARC092D] Two Faced Edges

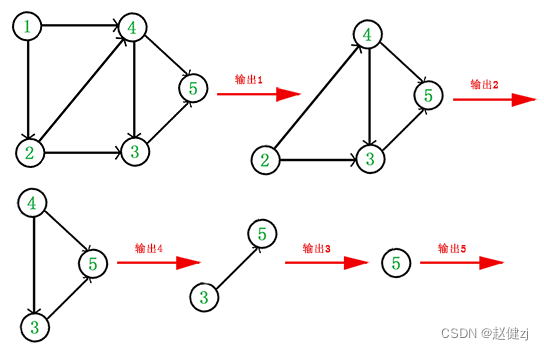
考虑强联通分量的本质，即其中任意两点 $u,v$ 都有一条 $u\to v$ 的路径，同时也有一条 $v\to u$ 的路径。

考虑转边强联通分量个数改变的情况，设有向边为 $(u,v)$：

• 有一条反向边 $(v,u)$ 且除了 $(u,v)$ 外无一条从 $u$ 到 $v$ 的路径，强联通分量个数减少。
• 无反向边 $(v,u)$ 且除了 $(u,v)$ 外有一条从 $u$ 到 $v$ 的路径，强联通分量个数增加。

个数不改变的情况即为：

• 有一条反向边 $(v,u)$ 且除了 $(u,v)$ 外有一条从 $u$ 到 $v$ 的路径，强联通分量个数减少。
• 无一条反向边 $(v,u)$ 且除了 $(u,v)$无一条从 $u$ 到 $v$ 的路径，强联通分量个数减少。

总结一下，就是考虑以下几个因素：

• 当前边是否有反向边，维护方法比较简单。
• 除当前边外是否有一条从 $u$ 到 $v$ 的路径，考虑染色判断，方法不讲。

时间复杂度 $\mathcal{O}(nm)$，可优化。

#include<bits/stdc++.h>

using namespace std;

//#define int long long
typedef long long ll;
#define ha putchar(' ')
#define he putchar('\n')

inline int read()
{
    
	int x = 0, f = 1;
	char c = getchar();
	while (c < '0' || c > '9')
	{
    
		if (c == '-')
			f = -1;
		c = getchar();
	}
	while (c >= '0' && c <= '9')
		x = x * 10 + c - '0', c = getchar();
	return x * f;
}

inline void write(int x)
{
    
	if(x < 0)
	{
    
		putchar('-');
		x = -x;
	}
	if(x > 9)
		write(x / 10);
	putchar(x % 10 + '0');
}

const int _ = 1010, M = 2e5 + 10;

int n, m, rt, u[M], v[M], flg[_];

bool f1[_][_], f2[_][_];

bitset<_> vis;

vector<int> d[_];

void dfs1(int u)
{
    
	vis.set(u);
	f1[rt][u] = 1;
	for(int v : d[u])
		if(!vis[v]) dfs1(v);
}

void dfs2(int u, int cxr, bool t)
{
    
	if(t) flg[u] = cxr;
	else f2[rt][u] = (flg[u] != cxr);
	vis.set(u);
	for(int v : d[u])
		if(!vis[v]) dfs2(v, cxr, t); 
} 

signed main()
{
    
	n = read(), m = read();
	for(int i = 1; i <= m; ++i)
	{
    
		u[i] = read(), v[i] = read();
		d[u[i]].push_back(v[i]);
	}
	for(int i = 1; i <= n; ++i)
	{
    
		vis.reset();
		rt = i;
		dfs1(i); 
	}
	for(int i = 1; i <= n; ++i)
	{
    
		vis.reset(), vis.set(i);
		memset(flg, 0, sizeof flg);
		int nw = d[i].size();
		rt = i;
		for(int j = 0; j < nw; ++j)
			if(!vis[d[i][j]]) dfs2(d[i][j], j + 1, 1);
		vis.reset(), vis.set(i);
		for(int j = nw - 1; j >= 0; --j)
			if(!vis[d[i][j]]) dfs2(d[i][j], j + 1, 0);
	}
	// for(int i = 1; i <= n; ++i)
	// {
    
	// for(int j = 1; j <= n; ++j) cout << f1[i][j] << " ";
	// cout << "\n";
	// }
	// cout << "\n";
		for(int i = 1; i <= n; ++i)
		{
    
			for(int j = 1; j <= n; ++j) cout << f2[i][j] << " ";
			cout << "\n";
		}
	for(int i = 1; i <= m; ++i)
		puts(f1[v[i]][u[i]] ^ f2[u[i]][v[i]] ? "diff" : "same");
	return 0;
}