当前位置:网站首页>Halcon uses points to fit a plane
Halcon uses points to fit a plane
2022-06-12 05:36:00 【Σίσυφος one thousand and nine hundred】
One 、 brief introduction
The project requires multiple points to fit a plane , Then we can calculate the distance from this point to the plane by using the points on other planes ,halcon There are ready-made fitting functions .
Two 、 Operator interpretation
* Enter point cloud data and generate 3D Model
gen_object_model_3d_from_points(X, Y, Z, ObjectModel3D)
* X, Y, Z The difference is x、y、z Set in direction
* ObjectModel3D It's output 3D Model * Fit the desired plane
fit_primitives_object_model_3d (ObjectModel3D, ['primitive_type','fitting_algorithm'], ['plane','least_squares_tukey'], ObjectModel3DOut)
*fit_primitives_object_model_3d( : : ObjectModel3D, ParamName, ParamValue : ObjectModel3DOut)
*ObjectModel3D: Input model
*ParamName: Fitted parameters :fitting_algorithm, max_radius, min_radius, output_point_coord, output_xyz_mapping, primitive_type
*ParamValue: Corresponding 'primitive_type'------'cylinder'( Cylinder ), 'sphere'( sphere ), 'plane'( Plane ). Corresponding 'primitive_type'------'least_squares', 'least_squares_huber', 'least_squares_tukey' Several least squares methods , Choose here plane and least_squares
*ObjectModel3DOut: Output plane
3、 ... and 、 Code demonstration
X:=[-0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04]
Y:=[-0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04]
Z:=[-0.0, -0.0, -0.0, -0.0, -0.1, -0.0, -0.0, -0.1, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, 0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0]
* Enter point cloud data and generate 3D Model
gen_object_model_3d_from_points(X, Y, Z, ObjectModel3D)
dev_open_window(0, 0, 512, 512, 'black', WindowHandle)
* Fit the desired plane
fit_primitives_object_model_3d (ObjectModel3D, ['primitive_type','fitting_algorithm'], ['plane','least_squares_tukey'], ObjectModel3DOut)
*fit_primitives_object_model_3d( : : ObjectModel3D, ParamName, ParamValue : ObjectModel3DOut)
*ObjectModel3D: Input model
*ParamName: Fitted parameters :fitting_algorithm, max_radius, min_radius, output_point_coord, output_xyz_mapping, primitive_type
*ParamValue: Corresponding 'primitive_type'------'cylinder'( Cylinder ), 'sphere'( sphere ), 'plane'( Plane ). Corresponding 'primitive_type'------'least_squares', 'least_squares_huber', 'least_squares_tukey' Several least squares methods , Choose here plane and least_squares
*ObjectModel3DOut: Output plane
visualize_object_model_3d (WindowHandle,[ObjectModel3D,ObjectModel3DOut], [],[], \
['color_0','color_1','alpha_1','disp_pose'], ['green','gray',0.5,'true'],'RectBOX', [], [], Pose)
* Get the normal vector ,Normal The first three values of are the unit normal vector
get_object_model_3d_params (ObjectModel3DOut, 'primitive_parameter', Normals)
Plane equation :ax+by+cz+d=0;
gen_object_model_3d_from_points(X, Y, Z, ObjectModel3D)
paraName:=['primitive_type', 'fitting_algorithm']
paraVal:=['plane', 'least_squares_tukey']
fit_primitives_object_model_3d(ObjectModel3D, ['primitive_type', 'fitting_algorithm'], ['plane', 'least_squares_tukey'], ObjectModel3DOut)
get_object_model_3d_params(ObjectModel3DOut, 'primitive_parameter', plane)
* Calculating plane equation (a,b,c,d)
A:= plane[0]
B:= plane[1]
C:= plane[2]
D:= plane[3]
So the distance between the point and the plane is :
Distance:=a*X + b*Y + c*Z - d
X:=[-0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04, -0.04, -0.03, -0.02, -0.01, 0.0, 0.01, 0.02, 0.03, 0.04]
Y:=[-0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.04, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.03, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, -0.01, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.03, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04, 0.04]
Z:=[-0.0, -0.0, -0.0, -0.0, -0.1, -0.0, -0.0, -0.1, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, 0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0, -0.0]
gen_object_model_3d_from_points(X, Y, Z, ObjectModel3D)
paraName:=['primitive_type', 'fitting_algorithm']
paraVal:=['plane', 'least_squares_tukey']
fit_primitives_object_model_3d(ObjectModel3D, ['primitive_type', 'fitting_algorithm'], ['plane', 'least_squares_tukey'], ObjectModel3DOut)
get_object_model_3d_params(ObjectModel3DOut, 'primitive_parameter', plane)
* Calculating plane equation (a,b,c,d)
A:= plane[0]
B:= plane[1]
C:= plane[2]
D:= plane[3]
x:=[-0.04, -0.03, -0.02, -0.01]
y:=[-0.04, -0.04, -0.04, -0.04]
z:=[-0.0, -1.0, 10.0, 30.0]
Distance:=A*x +B*y + C*z - D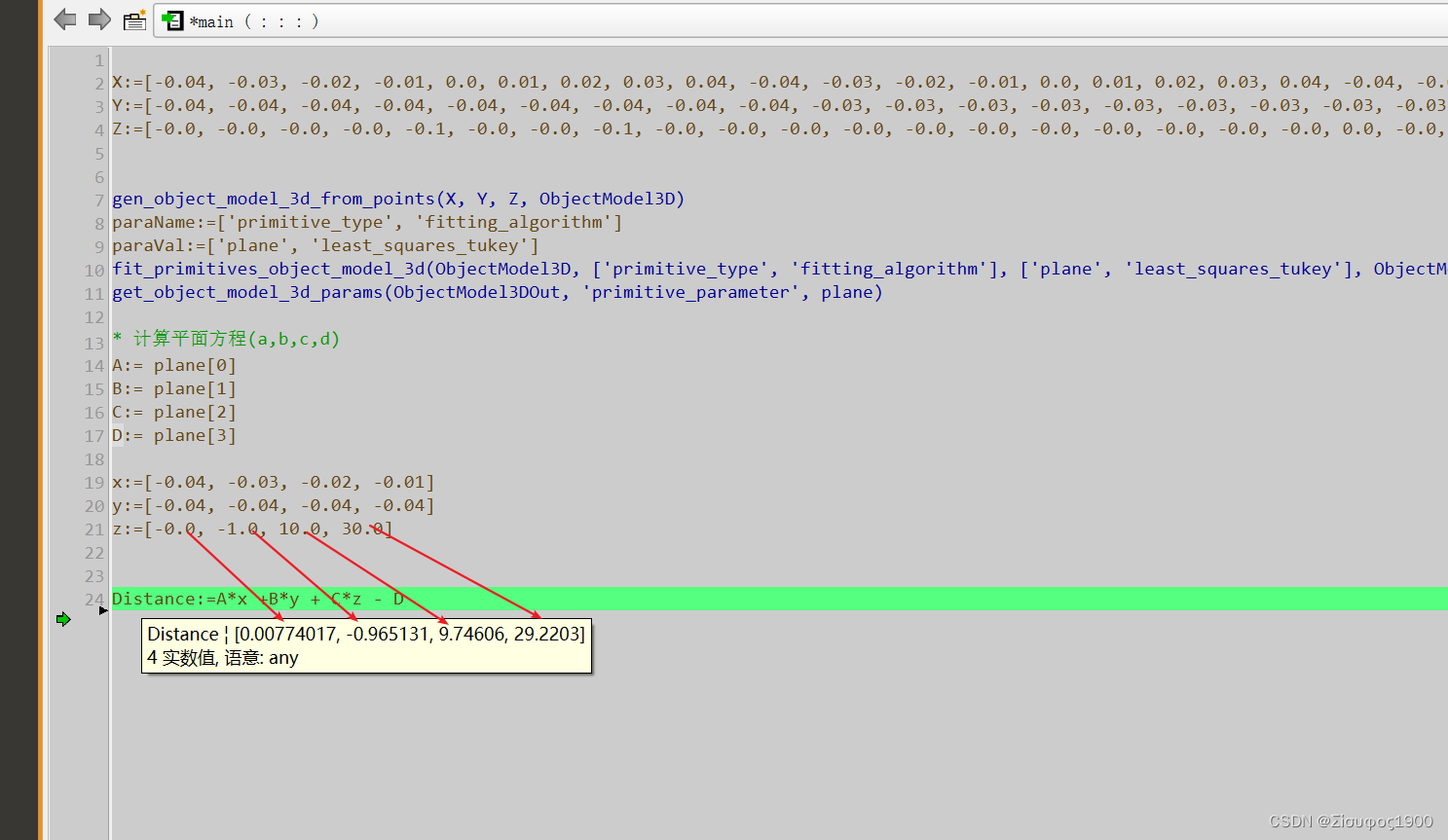
边栏推荐
- Greenplum [question 05] Greenplum streaming server custom client problem handling (increasing)
- Nbiot module me3616 at command mqtt connecting thingsboard
- Save the object in redis, save the bean in redis hash, and attach the bean map interoperation tool class
- 16. sum of the nearest three numbers
- Test work summary - performance test related issues
- 利用jieba库进行词频统计
- DMA RDMA technology details
- Introduction to redis cluster
- Thingsboard create RCP widget
- Vivado HLS introductory notes
猜你喜欢

How Wireshark decrypts WiFi data packets

Introduction to Internet Protocol

20000 word detailed reptile knowledge reserve, basic exercises of data collection and cleaning (I) reference answers to the first song

CCF noi2022 quota allocation scheme

yolov5
按键精灵的简单入门

Select gb28181, RTSP or RTMP for data push?

Servlet core technology

16. 最接近的三數之和

Word frequency statistics using Jieba database
随机推荐
57 - II. Continuous positive sequence with sum s
20. string representing numeric value
Analysis of pointer
43. Number of occurrences of 1 in 1 ~ n integers
C语言-数组的定义方式
29. print matrix clockwise
Field xxxxDAO in com. nero. hua. service. impl. LoginServiceImpl required a bean of type
国企为什么要上市
Research Report on market supply and demand and strategy of China's digital camera lens industry
GRE protocol details
SIM卡信号的驱动电流是多少mA,是否是可调节的?
Index fund summary
Detailed explanation of data envelopment analysis (DEA) (taking the 8th Ningxia provincial competition as an example)
20000 word detailed reptile knowledge reserve, basic exercises of data collection and cleaning (I) reference answers to the first song
Vivado HLS introductory notes
Simple introduction to key Wizard
基于tensorflow的校园绿植识别
yolov5
Serial port oscilloscope_ port_ Setup of plotter secondary development environment (including QT setup)
Quickly get PCA (principal component analysis) (principle code case)