CV learning notes - feature extraction

feature extraction

1. summary

Common features in images are edges 、 horn 、 Area, etc . Through the relationship between the attributes , Change the original feature space , For example, combine different attributes to get new attributes , Such processing is called feature extraction .

Be careful feature selection It is to select a subset from the original feature data set , Is an inclusive relationship , There is no change in the original feature space , Feature extraction is different , This is an important difference .

2. The main method

The main method of feature extraction ： Principal component analysis （PCA）

The main purpose of feature extraction ： Dimension reduction , Eliminate the feature of small amount of information, and then reduce the amount of calculation .

3. PCA

1. PCA Implementation of algorithm

According to the space transformation theory of vector , We can put a three-dimensional vector (x1,y1,z1) Change to (x2,y2,z2), Because after feature extraction , The feature space has changed , Suppose the base in the original feature space is (x,y,z), The base of the new space is (a,b,c), If in the new feature space , The projection of one dimension under the new substrate is close to 0, You can ignore , that , We can use it directly (a,b,c) To represent data （ Such as (x2,y2,z2) stay c The projections on the components are close to 0, that (a,b) Can represent this feature space ）, In this way, the dimension of data is reduced from three-dimensional space to two-dimensional space .

The key point is how to solve the new base (a,b,c)

Solving steps ：

• Zero mean the original data （ Centralization ）
• Find the covariance matrix
• Find the eigenvector and eigenvalue of the covariance matrix , Use these eigenvectors to form a new feature space .

2. Zero mean value （ Centralization ）

The process ： Centralization is to shift the center of the sample set to the origin of the coordinate system O On , Make the center of all data (0,0), That is, the variable minus its mean , Make the mean 0.

Purpose ： Make the data center of the sample set become (0,0), After centralizing data , The calculated direction can better reflect the original data .

The geometric meaning of dimensionality reduction ：

For a set of data , If its variance in a certain base direction is larger , It shows that the distribution of points is more scattered , Indicate the attribute represented in this direction （ features ） Can better reflect the source spatial data set . So when reducing dimension , The main purpose is to find a hyperplane that can maximize the variance of the distribution of data points , In this way, the data is scattered enough when it is displayed on the new coordinate axis .

The definition of variance ：

PCA The optimization goal of the algorithm is ：

• After dimensionality reduction, the variance of the same dimension is the largest
• The correlation between different dimensions is 0

3. Definition of covariance matrix

Definition ：

significance ： Measure the relationship between two attributes

When Cov(X, Y) >(<)(=) 0 when ,X And Y just ( negative )( No ) relevant

characteristic ：

• The covariance matrix calculates the covariance between different dimensions , Not between different samples .
• Each row of the sample matrix is a sample , Each column is a dimension , So the sample set should calculate the mean value by column .
• The diagonal of the covariance matrix is the variance of each dimension , That is to say （Cov(X,X) = D(X)）

Specially , Covariance matrix after data centralization , That is, the covariance matrix formula of the centralization matrix ：

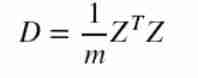
4. Find the eigenvalue and eigenmatrix of the covariance matrix

In fact, the solution of eigenvalues and eigenvectors , It is already a very skilled and general method in College Mathematics , So what does it mean in the image ？

Eigenvector ： That is, the features extracted from the image after the eigenvalue decomposition of the image matrix .

The eigenvalue ： Its corresponding characteristics （ Eigenvector ） Importance in the image .

Do eigenvalue decomposition of digital image matrix , In fact, it is extracting the features of this image , The extracted vector is the feature vector , The corresponding eigenvalue is the importance of this feature in the image . In linear algebra , A matrix is a linear transformation , Under normal circumstances, after a random linear transformation, the vector will lose the usual visible relationship with the vector before the transformation , The eigenvector is transformed linearly by using the original matrix , It is only multiplied by the eigenvector before transformation , in other words , The eigenvector is still under the transformation of the original matrix “ Keep it as it is. ”, So these vectors （ Eigenvector ） It can be used as the core representative of the matrix . therefore , A matrix （ linear transformation ） It can be completely expressed by its eigenvalue and eigenvector , This is because mathematically , All eigenvectors of this matrix form a set of bases of this vector space , The essence of matrix transformation is to transform things under one base into the space represented by another base .

give an example ：

For example, a 100x100 The image matrix of A After decomposition , You'll get one 100x100 The matrix of the eigenvectors of Q, And one. 100x100 Only the elements on the diagonal are not 0 Matrix E, This matrix E The element on the diagonal is the eigenvalue , And it is arranged from large to small （ modulus , For a single number , In fact, it is to take the absolute value ）, In other words, this image A It's extracted 100 Features , this 100 The importance of a feature is determined by 100 A number to indicate , this 100 A number is stored in the diagonal matrix E in .

5. Sort the eigenvalues

Method ：

Evaluate the model ,K Determination of value ：

Through the calculation of eigenvalues, we can get the percentage of principal components , To measure the quality of a model .

For the former K The calculation method of the amount of information retained by the eigenvalues is as follows ：

6. PCA Advantages and disadvantages of the algorithm

advantage ：

• Completely parameter free . stay PCA There is no need to consider the setting parameters or intervene in the calculation according to any empirical model , The final result is only relevant to the data , Independent of the user .
• use PCA Technology can reduce the dimension of data , At the same time, the new “ Principal component ” The importance of vectors , Take the most important part of the front as needed , Omit the following dimensions , It can reduce the dimension and simplify the model or compress the data . At the same time, the information of the original data is maintained to the greatest extent .
• The principal components are orthogonal , It can eliminate the interaction between the components of the original data .
• The calculation method is simple , Easy to implement on computer .

shortcoming ：

• If the user has some prior knowledge of the observation object , Have mastered some characteristics of the data , However, it is impossible to intervene the processing process by parameterization and other methods , May not get the expected effect , It's not efficient either .
• Principal components with small contribution rate may contain important information about sample differences .

---

Personal study notes , Only exchange learning , Reprint please indicate the source ！