当前位置:网站首页>决策树和随机森林
决策树和随机森林
2022-08-03 09:43:00 【weixin_961876584】
认识决策树
- 决策树思想的来源非常朴素,程序设计中的条件分支结构就是if-else结构,最早的决策树就是利用这类结构分割数据的一种分类学习方法
- 决策树:是一种树形结构,其中每个内部节点表示一个属性上的判断,每个分支代表一个判断结果的输出,最后每个叶节点代表一种分类结果,本质是一颗由多个判断节点组成的树。
- 相亲样例。比如:你母亲要给你介绍男朋友,是这么来对话的:
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。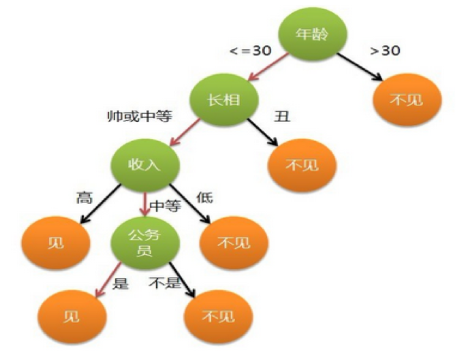
- 想一想这个女生为什么把年龄放在最上面判断!!!!!!!!!
上面案例是女生通过定性的主观意识,把年龄放到最上面,那么如果需要对这一过程进行量化,该如何处理呢?
此时需要用到信息论中的知识:信息熵,信息增益
决策树分类原理
熵
- 物理学上,熵 Entropy 是“混乱”程度的量度。系统越有序,熵值越低;系统越混乱或者分散,熵值越高
- 信息理论:数据越集中的地方熵值越小,数据越分散的地方熵值越大;数据量一致时,系统越有序,熵值越低;系统越混乱或者分散,熵值越高
信息熵
- 假如事件A的分类划分是 ( A 1 , A 2 , . . . , A n ) (A_1,A_2,...,A_n) (A1,A2,...,An),每部分发生的概率是 ( p 1 , p 2 , . . . , p n ) (p_1,p_2,...,p_n) (p1,p2,...,pn),那信息熵定义为公式如下:(log是以2为底,lg是以10为底)
H ( A ) = − ∑ k = 1 n p k log 2 p k H(A)=-\sum_{k=1}^np_k\log_2p_k H(A)=−k=1∑npklog2pk
决策树的划分依据一 :信息增益(ID3)
信息增益概念
- 信息增益:以某特征划分数据集前后的熵的差值。熵可以表示样本集合的不确定性,熵越大,样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。
概率定义
- 特征A对训练数据集D的信息增益g(D,A),定义为
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A)=H(D)-H(D|A) g(D,A)=H(D)−H(D∣A)
设训练数据集D有K个类别(目标值),每个类别的个数分别为 C 1 , C 2 , . . . C K C_1,C_2,...C_K C1,C2,...CK,则
H ( D ) = − ∑ k = 1 K ∣ C k ∣ ∣ D ∣ log 2 ∣ C k ∣ ∣ D ∣ H(D)=-\sum_{k=1}^K\frac{|C_k|}{|D|}\log_2\frac{|C_k|}{|D|} H(D)=−k=1∑K∣D∣∣Ck∣log2∣D∣∣Ck∣
设特征A有n个分类,数据集D按照特征A可以分成n部分 D 1 , D 2 , . . . D n D_1,D_2,...D_n D1,D2,...Dn,则
H ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ∑ k = 1 K ∣ D i k ∣ ∣ D i ∣ log ∣ D i k ∣ ∣ D i ∣ H(D|A)=\sum_{i=1}^n\frac{|D_i|}{|D|}H(D_i)=-\sum_{i=1}^n\frac{|D_i|}{|D|}\sum_{k=1}^K\frac{|D_{ik}|}{|D_i|}\log\frac{|D_{ik}|}{|D_i|} H(D∣A)=i=1∑n∣D∣∣Di∣H(Di)=−i=1∑n∣D∣∣Di∣k=1∑K∣Di∣∣Dik∣log∣Di∣∣Dik∣
注:信息增益表示得知特征X的信息而使得类Y的信息熵减少的程度。信息增益大的特征被认为是更重要的
缺点
- ID3算法在选择根节点和各内部节点中的分支属性时,采用信息增益作为评价标准。信息增益的缺点是倾向于选择取值较多的属性,在有些情况下这类属性可能不会提供太多有价值的信息
- ID3算法只能对描述属性为离散型属性的数据集构造决策树
决策树的划分依据二:信息增益率(C4.5)
定义
- 信息增益偏向特征值较多的特征,为了克服这一缺点,使用信息增益率
- 特征A对训练数据集D的信息增益率 g r a t i o ( D , A ) g_{ratio}(D,A) gratio(D,A),定义为
g r a t i o ( D , A ) = g ( D , A ) H A ( D ) g_{ratio}(D,A)=\frac{g(D,A)}{H_A(D)} gratio(D,A)=HA(D)g(D,A)
H A ( D ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ log ∣ D i ∣ ∣ D ∣ H_A(D)=-\sum_{i=1}^n\frac{|D_i|}{|D|}\log \frac{|D_i|}{|D|} HA(D)=−i=1∑n∣D∣∣Di∣log∣D∣∣Di∣
H A ( D ) H_A(D) HA(D)称为特征A的固有值
优缺点
- 优点: 产生的分类规则易于理解,准确率较高。
- 缺点:
- 在构造树的过程中,需要对数据集进行多次的顺序扫描和排序,因而导致算法的低效。
- C4.5只适合于能够驻留于内存的数据集,当训练集大得无法在内存容纳时程序无法运行。
- 信息增益率对可取值较少的特征值有所偏好
决策树的划分依据三:基尼系数增益(CART用的最多)
- 基尼值
G i n i ( D ) = 1 − ∑ k = 1 K ( ∣ D i ∣ ∣ D ∣ ) 2 Gini(D)=1-\sum_{k=1}^K(\frac{|D_i|}{|D|})^2 Gini(D)=1−k=1∑K(∣D∣∣Di∣)2
- 基尼系数增益
G i n i a d d = G i n i ( D ) − G i n i ( D ∣ A ) Gini_{add}=Gini(D)-Gini(D|A) Giniadd=Gini(D)−Gini(D∣A)
G i n i ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ G i n i ( D i ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ( 1 − ∑ k = 1 K ( ∣ D i k ∣ ∣ D i ∣ ) 2 ) Gini(D|A)=\sum_{i=1}^n\frac{|D_i|}{|D|}Gini(D_i)=-\sum_{i=1}^n\frac{|D_i|}{|D|}(1-\sum_{k=1}^K(\frac{|D_{ik}|}{|D_i|})^2) Gini(D∣A)=i=1∑n∣D∣∣Di∣Gini(Di)=−i=1∑n∣D∣∣Di∣(1−k=1∑K(∣Di∣∣Dik∣)2)
- 可进行分类和回归
- CART算法相比C4.5算法的分类方法,采用了简化的二叉树模型,同时特征选择采用了近似的基尼系数来简化计算。
- C4.5不一定是二叉树,但CART一定是二叉树。
决策树对泰坦尼克号进行预测生死
导入包
from sklearn.model_selection import train_test_split, GridSearchCV #train_test_split 划分训练集和测试集,GridSearchCV交叉验证和网格搜索
from sklearn.preprocessing import StandardScaler
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.ensemble import RandomForestClassifier
import pandas as pd
import numpy as np
from sklearn.metrics import roc_auc_score #求分类AUC指标
导入数据
# 获取数据
titan = pd.read_csv("./data/titanic.txt")
titan.info()
结果:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1313 entries, 0 to 1312
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 row.names 1313 non-null int64
1 pclass 1313 non-null object
2 survived 1313 non-null int64
3 name 1313 non-null object
4 age 633 non-null float64
5 embarked 821 non-null object
6 home.dest 754 non-null object
7 room 77 non-null object
8 ticket 69 non-null object
9 boat 347 non-null object
10 sex 1313 non-null object
dtypes: float64(1), int64(2), object(8)
memory usage: 113.0+ KB
找出特征值和目标值
# 处理数据,找出特征值和目标值
x = titan[['pclass', 'age', 'sex']]
y = titan['survived']
x.describe(include=object)
结果:
pclass sex
count 1313 1313
unique 3 2
top 3rd male
freq 711 850
缺失值处理和数据集划分
# 一定要进行缺失值处理,填为均值
x['age'].fillna(x['age'].mean(), inplace=True)
# 分割数据集到训练集合测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25, random_state=4)
x_train.head()
结果:
pclass age sex
598 2nd 30.000000 male
246 1st 62.000000 male
905 3rd 31.194181 female
300 1st 31.194181 female
509 2nd 64.000000 male
one hot编码
# 进行处理(特征工程)特征-》类别-》one_hot编码
dict = DictVectorizer(sparse=False)
# 这一步是对字典进行特征抽取,to_dict可以把df变为字典,records代表列名变为键
x_train = dict.fit_transform(x_train.to_dict(orient="records"))
print(type(x_train))
print(dict.get_feature_names())
print('-' * 50)
x_test = dict.transform(x_test.to_dict(orient="records"))
print(x_train)
结果:
<class 'numpy.ndarray'>
['age', 'pclass=1st', 'pclass=2nd', 'pclass=3rd', 'sex=female', 'sex=male']
--------------------------------------------------
[[30. 0. 1. 0. 0. 1. ]
[62. 1. 0. 0. 0. 1. ]
[31.19418104 0. 0. 1. 1. 0. ]
...
[34. 0. 1. 0. 0. 1. ]
[46. 1. 0. 0. 0. 1. ]
[31.19418104 0. 0. 1. 0. 1. ]]
决策树预测
# 用决策树进行预测,修改max_depth试试
dec = DecisionTreeClassifier()
#训练
dec.fit(x_train, y_train)
# 预测准确率
print("预测的准确率:", dec.score(x_test, y_test))
# 导出决策树的结构
export_graphviz(dec, out_file="tree.dot",
feature_names=['年龄', 'pclass=1st', 'pclass=2nd', 'pclass=3rd', '女性', '男性'])
结果:预测的准确率: 0.8085106382978723
随机森林
# 随机森林进行预测 (超参数调优),n_jobs充分利用多核的一个参数
rf = RandomForestClassifier(n_jobs=-1)
# 120, 200, 300, 500, 800, 1200,n_estimators森林中决策树的数目,也就是分类器的数目
# max_samples 是最大样本数
#bagging类型
param = {
"n_estimators": [2000, 5000], "max_depth": [2, 3, 5, 8, 15, 25]}
# 网格搜索与交叉验证
gc = GridSearchCV(rf, param_grid=param, cv=3)
gc.fit(x_train, y_train)
print("准确率:", gc.score(x_test, y_test))
print("查看选择的参数模型:", gc.best_params_)
print("选择最好的模型是:", gc.best_estimator_)
结果:
准确率: 0.8358662613981763
查看选择的参数模型: {
'max_depth': 3, 'n_estimators': 2000}
选择最好的模型是: RandomForestClassifier(max_depth=3, n_estimators=2000, n_jobs=-1)
随机森林详细信息见《集成学习》
边栏推荐
- SQL Daily Practice (Nioke New Question Bank) - Day 5: Advanced Query
- Rabbit and Falcon are all covered, Go lang1.18 introductory and refined tutorial, from Bai Ding to Hongru, the whole platform (Sublime 4) Go lang development environment to build EP00
- Scala parallel collections, parallel concurrency, thread safety issues, ThreadLocal
- CRT命令按键
- cert-manager使用
- 别人都不知道的“好用”网站,让你的效率飞快
- mysqldump导出提示:mysqldump [Warning] Using a password on the command line interface can be insecure
- 索引(三)
- mysql 运行的时候 报错
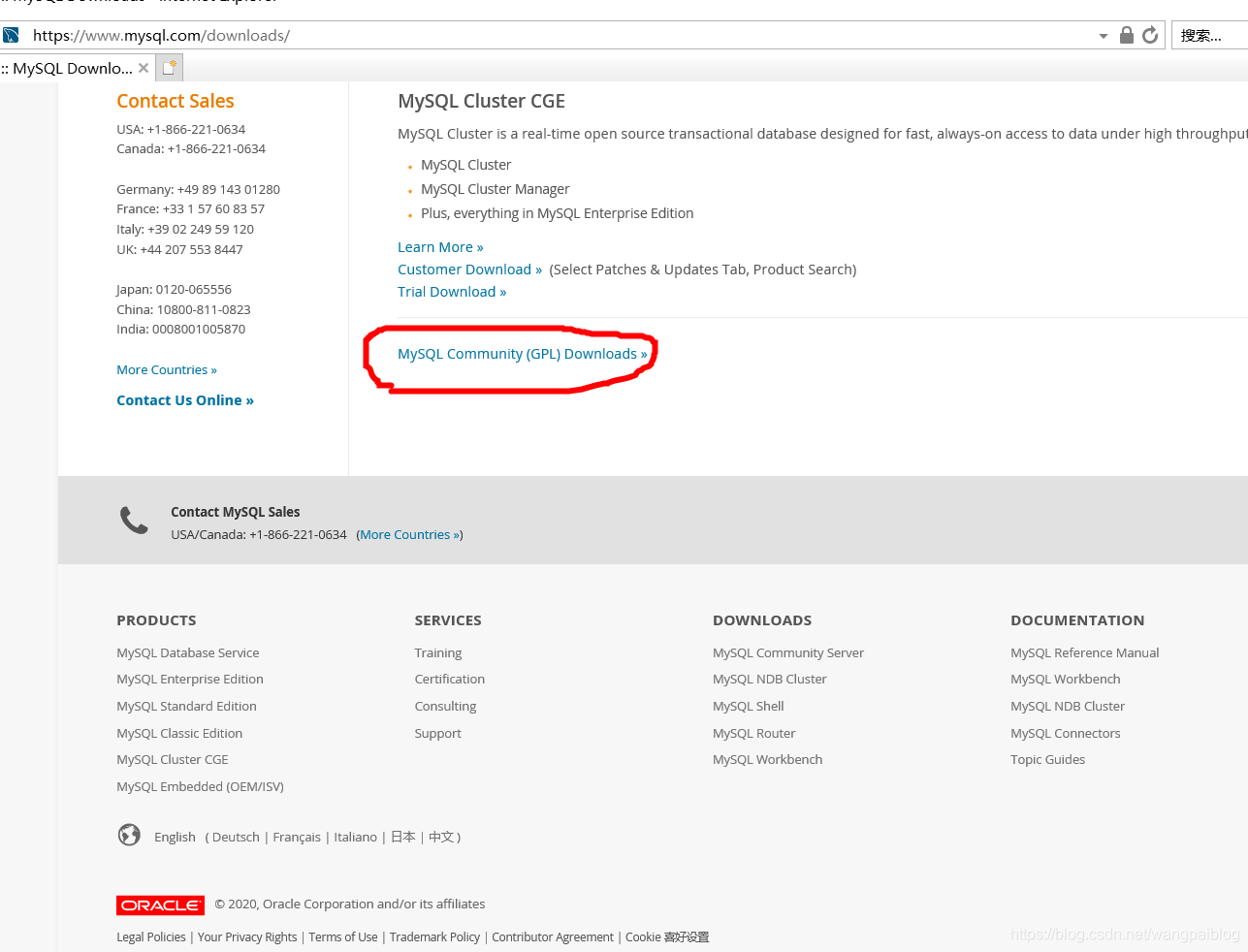
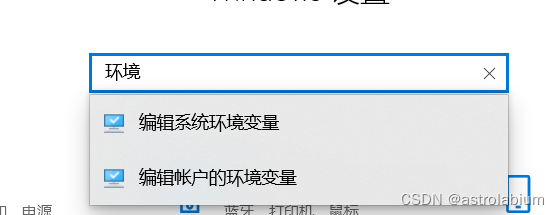
- mysql8安装步骤教程
猜你喜欢
随机推荐
2022最新整理软件测试常见面试题附答案
【LeetCode】zj面试-把字符串转换成整数
Promise 1: Basic Questions
MySQL的分页你还在使劲的limit?
System io statistics
oracle ASM磁盘空间的查看
milvus
MySQL的主从复制
WinCheck Script
Oracle数据库表空间整理回收与释放操作
C language two-dimensional array is called with one-dimensional array
MySQL 如何修改SQL语句,去掉语句中的or
【快手面试】Word2vect生成的向量,为什么可以计算相似度,相似度有什么意义?
scala减少,reduceLeft reduceRight,折叠,foldLeft foldRight
AUC的两种计算方式
子查询和关联查询的区别
js中最简单base64图片流实现自动下载
10 minutes to get you started chrome (Google) browser plug-in development
Redis cluster concept and construction
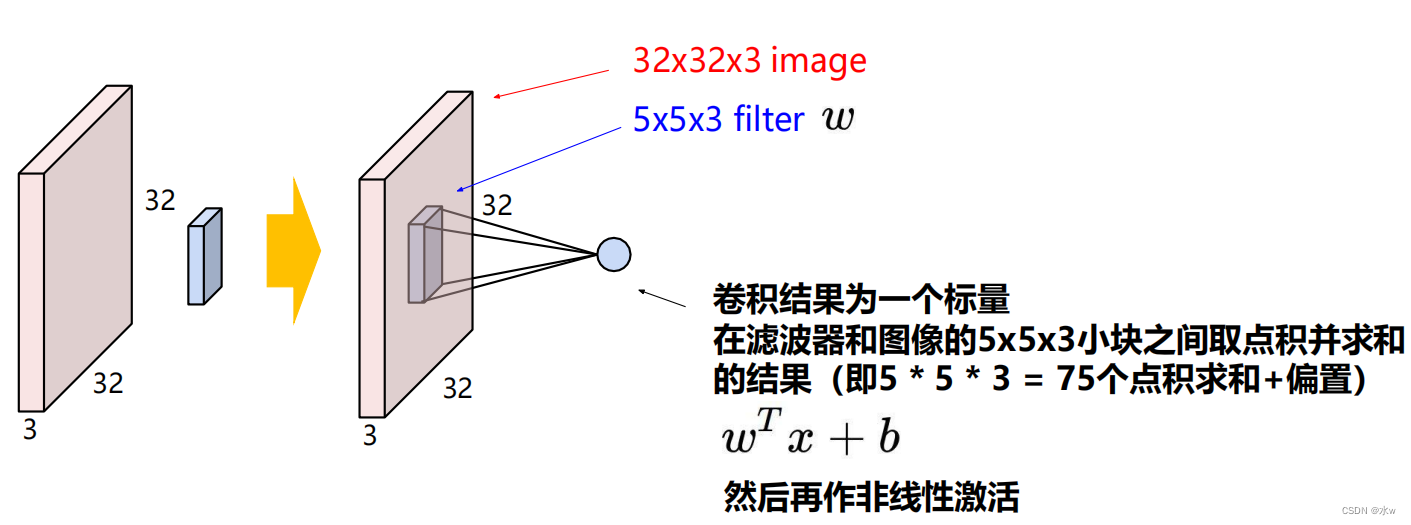
10 Convolutional Neural Networks for Deep Learning 2