Amélioration de la 3dsc par HSC

Dans le blog précédent(Sur les caractéristiques contextuelles de la forme 3D3DSCThéorie et application),Nous avons présenté3DSCPrincipes de conception et détails de mise en oeuvre,Et cette caractéristique est limitée dans une certaine mesure aux défauts de l'estimation normale.En fait,Dans la littérature[1]Moyenne,L'auteur propose3DSCEn même temps,La solution correspondante est également donnée,Pour atténuer3DSCLes défauts intrinsèques de,C'est - à - dire les caractéristiques du contexte de forme harmoniqueHarmonic shape contexts(HSC).Aujourd'hui, nous allons étudier concrètementHSCPrincipes et mise en œuvre.

---

Un.. Introduction

PourHSCUne explication simple et directe,Oui.3DSCL'information réalise la transformation du domaine de fréquence.En raison de l'erreur dans l'estimation normale des données de nuages ponctuels,L'emplacement de l'espace sphérique local qui provoque certains points peut produire une exception.Voilà.3DSCL'extraction des caractéristiques entraîne des facteurs d'instabilité.D'après les propriétés du nuage ponctuel,Sauf dans les zones frontalières,Sinon, la distribution normale des nuages ponctuels doit être continue,Ou la transformation normale est lisse.Alors,Pour les zones non frontalières,3DSCLa variation correspondante des données de l'histogramme doit également être lisse.Si une perturbation importante ou une anomalie des données se produit dans une zone non délimitée,On peut donc supposer qu'il y a un problème avec l'estimation normale de la région.Donc,, Une solution intuitive consiste à utiliser une analyse du domaine de fréquence pour réduire les anomalies statistiques causées par des perturbations aléatoires . Sur la base de cette idée ,HSCA été proposé.

Basé sur3DSCHistogramme établi,HSC Comme échantillon d'échantillonnage , Pour sphère shell( Je ne connais pas la traduction exacte ,Combiner le contexte, C'est comme s'il s'agissait d'un bin L'espace de la cellule sphérique ), Calculer une transformation Harmonique sphérique .HSC Le descripteur peut être considéré comme l'amplitude de la transformation harmonique , Invariance de rotation par rapport à l'azimut , Ainsi, les degrés de liberté liés à l'azimut peuvent être supprimés .En bas, Commençons par une introduction HSC Les étapes spécifiques de l'extraction de l'opérateur .

---

2.. HSC Extraction de l'opérateur

Toute équation peut être exprimée comme la somme d'un ensemble de fonctions de base harmoniques sphériques ( Ceci est similaire à la généralisation de la transformation de Fourier en 3D , C'est - à - dire qu'aucune fonction ne peut être représentée comme une combinaison d'un ensemble de fonctions trigonométriques ). Le calcul de la somme est considéré comme une transformation harmonique f, Mathématiquement exprimé comme ：

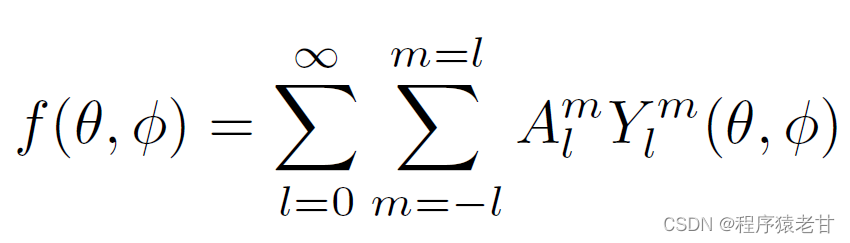
Y_l^m Pour la fonction de base mentionnée précédemment . Une caractéristique importante de cette transformation est de convertir la transformation de rotation en azimut en une transformation de phase dans le domaine de fréquence . Coefficient harmonique ||A_l^m|| N'est pas affecté par le changement d'angle de direction . Basé sur la transformation harmonique fDéfinitions,Union3DSCDebinDonnées, Donne un pour shellFonction defi,Les définitions sont les suivantes:：

Dans le domaine des fréquences,j La transformation d'angle directionnel représentée est considérée comme un déplacement influencé par un signal indépendant .Comme dans la littérature[2]Mentionné, Une bande passante est définie ici b, Et ne stocke que b Partie basse fréquence ,Ajouter àHSC, Calculé comme suit ：

Pour toute fonction réelle , ||A_l^m||=||A_l^-m||,QuandmMoins de0Heure, Facteur de rejet ||A_l^m||. C'est ainsi que HSCLa dimension estKb(b+1)/2.Attention!, La Division de l'azimut et de la différence de position n'affecte pas HSCDimension de(Je comprends.KAvecb C'est déjà l'information du domaine de fréquence , Ça n'a rien à voir avec la Division des données spatiales ).HSC Avec un descripteur invariant de rotation SH[2]Autres.La différence est,SH Est utilisé pour décrire les caractéristiques globales de la forme .En comparaison,HSC L'amplitude des composants individuels du domaine de fréquence est conservée , La description des caractéristiques est donc plus détaillée .

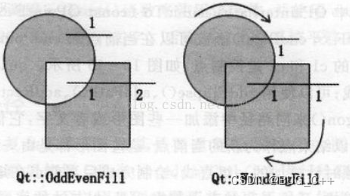
Fig.1 Un schéma est donné ,Pour visualiserHSC Propriétés invariantes de rotation de .Parmi eux, La zone rose du sous - Diagramme droit représente un rayon défini par shellRégion, Quand on calcule les données du domaine de fréquence pour cette zone , Sélectionnez une normale différente ,Il y aura une différence.SCExpression, Comme le signal rouge du sous - Diagramme de gauche , La distribution des données est décalée .Mais, Du point de vue du domaine de fréquence , Ce décalage dans le domaine temporel n'affecte pas la représentation des données dans le domaine de fréquence . Deux signaux du Domaine temporel qui semblent différents , Après transformation de Fourier , Obtenir exactement la même expression de domaine de fréquence .Donc,, Construit dans le domaine des fréquences HSC Avec Invariance rotationnelle .

 Fig.1. HSC Schéma bidimensionnel des caractéristiques du domaine de fréquence .

En distribuant les données des points spatiaux , Représentation du signal convertie en domaine de fréquence ,HSCDans une certaine mesure.3DSC Le problème des perturbations aléatoires . Représentation des caractéristiques dans le domaine des fréquences , Meilleure robustesse pour la rotation , Plus d'incarnation de chaque shell Rapidité et lenteur de la transformation de la distribution des données , Plutôt que la distribution des données elle - même .Donc,, Obtenu par transformation harmonique , Basé sur la représentation des signaux du domaine de fréquence HSC,Dans une certaine mesure.3DSC Questions sensibles à la rotation .

---

Résumé

HSCPour résoudre3DSC Affecté par l'estimation normale , Questions sensibles à la rotation . En changeant l'information correspondant à l'angle de phase , Mappé dans le domaine de fréquence correspondant , Obtenir des informations de phase dans le domaine des fréquences , On obtient ensuite une représentation caractéristique de la robustesse rotationnelle .Mais je pense queHSC Solutions sensibles à la rotation , Un peu insatisfaisant . La transformation du domaine de fréquence a en fait causé une perte d'information , Et encore moins dans le domaine des fréquences . Je n'ai pas trouvé HSCCode de mise en œuvre pour,PourHSC Il y a très peu d'informations sur .C'est sur le côté.HSC Pas dans la pratique pour 3DSC Apporter des améliorations essentielles .Mais,HSC Les idées proposées sont dignes de référence , Essayez de résoudre le problème de rotation dans le domaine des fréquences , Il y a encore des choses à faire .

---

Reference

[1] A. Frome, et al. Recognizing objects in range data using regional point descriptors [C]. ECCV, 2004: 224-237.

[2] K. M, et al. Rotation invariant spherical harmonic representation of 3d shape descriptors. ACM SIGGRAPH symposium on Geometry processing, 2003:156-164.