【点云处理之论文狂读经典版12】—— FoldingNet: Point Cloud Auto-encoder via Deep Grid Deformation

摘要

• 背景： 目前的深度学习网络都是通过点集的形式直接处理点云，并且在分类和分割的点云处理任务上取得了不错的成绩
• 问题： 点云在无监督学习下的挑战
• 方法： 本文提出了一种端到端式的深度auto-decoder
• 细节：
  1. 在encoder端，使用一种基于Graph的增强方法提升PointNet的局部结构提取能力
  2. 在decoder端，使用基于folding的方法将一个规范的2D网络变形成点云的表面形状，在获取细节结构的同时还会导致很低的重建误差
• 优势：
  1. 所提出decoder使用的参数数量很少，但是能够产生更具鉴别性的表示
  2. 所提出的decoder是一个通用结构，在理论上能够根据2D网格重建任意点云的表面形状
• 代码：
  1. http://www.merl.com/research/license#FoldingNet
  2. https://github.com/AnTao97/UnsupervisedPointCloudReconstruction PyTorch版本 点云无监督方法比较

引言

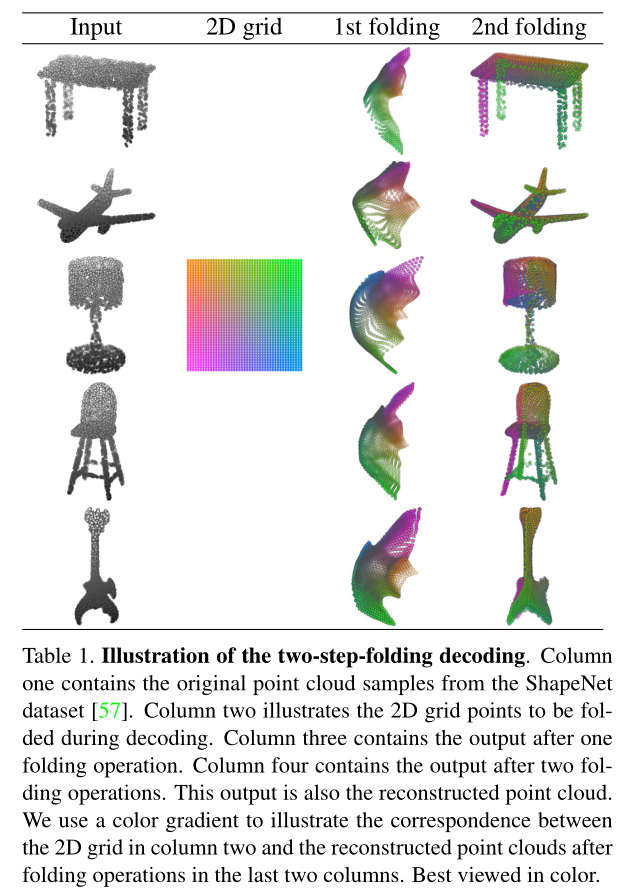
如表1所示，在decoder阶段，我们想要施加一个“虚拟的外力”，将2D网格 变形 成3D物体的表面形状，这种变形应该受到网格neighborhood相互连接的影响和约束。

FoldingNet Auto-encoder on Point Cloud

Auto-encoder的pipeline如图2所示。encoder的输入是一个$n\times 3$的矩阵，矩阵的每一行包含了3D点云的位置$(x,y,z)$。输出是一个$m\times 3$的矩阵，表示重建后点的位置。重建后点的数量$m$没必要与原始点云的数量$n$相同。假设输入包含了点集$S$，重建后的点集为$\hat{S}$，那么重建误差可以使用 extended Chamfer distance进行计算：
$$\begin{array}{rl}{d}_{CH}(S,\hat{S})=\max & \{\frac{1}{|S|}\sum _{\mathbf{x}\in S}\underset{\hat{\mathbf{x}}\in \hat{S}}{\min }\Vert \mathbf{x}-\hat{\mathbf{x}}{\Vert }_2,\frac{1}{|\hat{S}|}\sum _{\hat{\mathbf{x}}\in \hat{S}}\underset{\mathbf{x}\in S}{\min }\Vert \hat{\mathbf{x}}-\mathbf{x}{\Vert }_2\}\end{array}$$
${\min }_{\hat{\mathbf{x}}\in \hat{S}}\Vert \mathbf{x}-\hat{\mathbf{x}}{\Vert }_2$强制原始点云中的任意的3D点 $\mathbf{x}$ 都能够和重建后点云中的3D点$\hat{\mathrm{x}}$相匹配，${\min }_{\mathbf{x}\in S}\Vert \hat{\mathbf{x}}-\mathbf{x}{\Vert }_2$正好和上面反过来。max操作强制从$S$ 到$\hat{S}$和从$\hat{S}$ 到$S$的距离必须同时小。encoder计算了每个输入点云的表示codeword，那么decoder就会根据这个codeword重建点云。在本文中，codeword的长度被设置为512。

Graph-based Encoder Architecture

基于Graph的encoder遵循着和 KCNet 一样的设计，该网络使用点云的neighborhood graphs进行有监督学习。encoder是多个MLP层和基于Graph的max pooling层拼接而成的。Graph以输入点集的位置作为顶点，再通过KNN得到K-NNG。实验中，将$K$设置成16。

1. 首先，对于每个点$v$，计算其大小为$3\times 3$的局部协方差矩阵，并将其向量化为$1\times 9$的向量。$v$的局部协方差是利用K-NNG中$v$(包括$v$)的one-hop neighbors 点的三维位置来计算的；
2. 将大小为$n\times 3$的位置矩阵和大小为$n\times 9$的局部协方差矩阵进行拼接，得到大小为$n\times 12$的矩阵作为输入，放到3层的MLP里；
3. MLP的输出被放入两个连续的graph层中，其中每一层都对节点的邻域使用max pooling；
   具体而言，假设K-NN Graph有邻接矩阵$\mathbf{A}$和输入矩阵$\mathbf{X}$，那么输出矩阵为：
   $$\mathbf{Y}={\mathbf{A}}_{\max }(\mathbf{X})\mathbf{K}$$
   其中$\mathbf{K}$是特征映射矩阵，矩阵${\mathbf{A}}_{\max }(\mathbf{X})$的第$(i,j)$个元素为：
   $${\left({\mathbf{A}}_{\max }(\mathbf{X})\right)}_{ij}=\mathrm{ReLU}\left(\underset{k\in \mathcal{N}(i)}{\max }{x}_{kj}\right)$$
   上式中的局部max pooling操作本质上是在计算基于graph结构的局部signature，这个signature可以表示局部邻域的(聚合后)拓扑信息。通过拼接基于graph的max pooling层，网络将拓扑信息传播到更大的区域中。

Folding-based Decoder Architecture

所提出的decoder使用了两个连续3层的MLP，令2D网格更“贴合”输入点云的形状。输入codeword是通过上一节中的encoder得到的。

1. 在将codeword输入到decoder中前，要将该codeword复制$m$次，变成大小为$m\times 512$的矩阵，然后和包含了$m$个网格的点坐标进行拼接，拼接的结果是一个大小为$m\times 514$的矩阵。
2. 将拼接后的矩阵作为输入，以行为单位进行处理，放入一个3层MLP，输出是大小为$m\times 3$的矩阵。
3. 将上面输出的矩阵再与重复的codeword矩阵进行拼接，再放入一个3层的MLP，最后得到大小为$n\times 3$的重建后输出。

再本文中，$n$取2048，$m$取平方后的数，2025。

定义

将重复codeword和低维网格点的拼接，再接一个point-wise MLP的操作称为一个folding。

folding操作本质上是一个通用的2D到3D的映射。为了直观地理解为何folding操作是一个通用的2D到3D的映射，记矩阵$\mathbf{U}$为输入的2D网格点，$\mathbf{U}$的每行是一个二维网格点；记$\mathbf{U}$的第$i$行为${\mathbf{u}}_i$，从encoder中得到的codeword为$\mathbf{\theta }$。那么在拼接后，输入到MLP中矩阵的第$i$行可以写成$\left[{\mathbf{u}}_i,\mathbf{\theta }\right]$。由于MLP是并行地在输入矩阵的每一行上进行处理，所以输出矩阵的第$i$行可以写成 $f\left(\left[{\mathbf{u}}_i,\mathbf{\theta }\right]\right)$，其中$f$表示由MLP构成的函数。该函数可以看成一个参数化的高维函数，其中codeword $\mathbf{\theta }$是引导函数结构的参数（folding operation）。由于MLP在估算非线性函数上能力很强，所以它们可以在2D网格上进行更好的folding operation。高维的codeword本质上存储着一种结构特征，迫使2D网格进行变形，使得folding operation更加的多样化。

所提出的decoder有两个folding operation。第一个folding operation是将2D网格从2D空间变换到3D空间，第二个folding operation是在3D空间内进行变换，见表1。

理论分析

理论1

所提出的encoder结构是排序不变的，即如果输入点云矩阵的行是可以任意排序的，得到的codeword仍然保持不变。

理论2

存在一个两层的MLP，能够使用folding操作将一个二维grid重构成任意的点云。

实验

Visualization of the Training Process

Point Cloud Interpolation

Point Cloud Interpolation

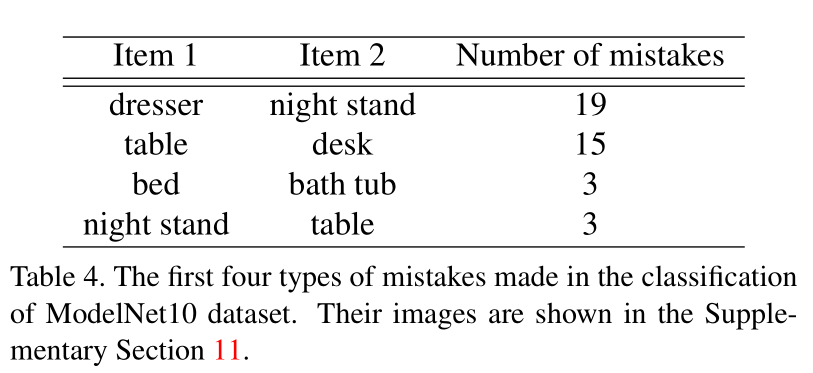
Transfer Classification Accuracy

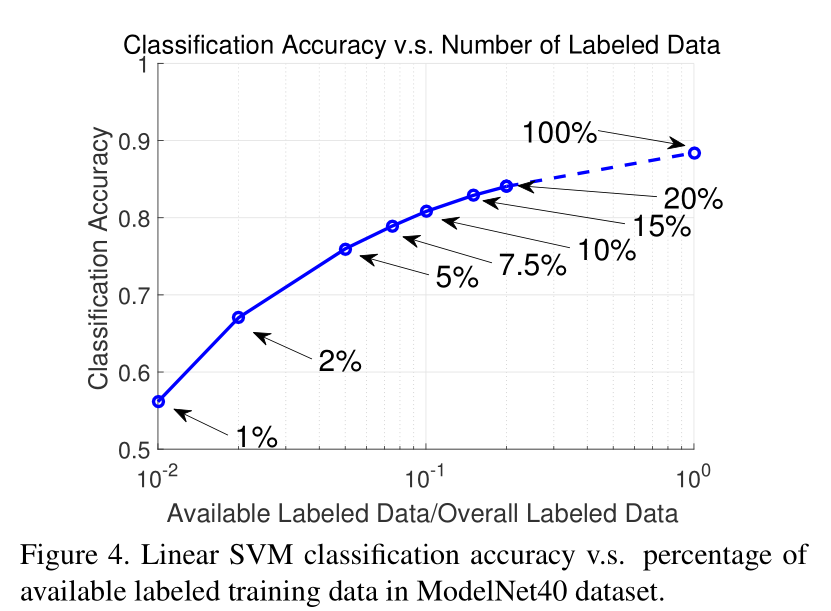
Semi-supervised Learning:What Happens when Labeled Data are Rare

Effectiveness of the Folding-Based Decoder

生词

1. downside n. 缺点，不足之处