当前位置:网站首页>[eight sorting ③] quick sorting (dynamic graph deduction Hoare method, digging method, front and back pointer method)
[eight sorting ③] quick sorting (dynamic graph deduction Hoare method, digging method, front and back pointer method)
2022-07-02 00:44:00 【Living_ Amethyst】
Catalog
One 、 Bubble sort (Bubble Sort)
A common way to divide an interval into left and right halves according to the reference value :
3、 Front and back pointer method
Non recursive implementation of quick sorting
One 、 Bubble sort (Bubble Sort)
The principle of bubble sorting
From left to right , Compare adjacent elements . Compare one round at a time , You will find the largest or smallest in the sequence . This number will appear from the far right of the sequence .
- Take sorting from small to large as an example ,
- Compare adjacent elements . If the first one is bigger than the second one , Just swap them .
- Do the same for each pair of adjacent elements , From the beginning of the first couple to the end of the last couple . After this step , The last element will be the maximum number .
- Repeat the above steps for all elements , Except for the last one .
- Keep repeating the above steps for fewer and fewer elements each time , Until there's no pair of numbers to compare .
- After the first round of comparison , The largest of all numbers will float to the far right ; After the second round of comparison , The second largest of all numbers will float to the penultimate position …… Just compare it round by round , Finally, sort from small to large .

When is the fastest
When the input data is already in positive order ( It's all in order , Do I need you to bubble sort ?)
When is the slowest
When the input data is in reverse order ( Write a for loop trans Just output the data , Why do you want to bubble sort it ?)
Algorithm stability
Bubble sort is to move small elements forward or to move large elements back . Comparison is the comparison of two adjacent elements , The exchange also happens between these two elements . therefore , If two elements are equal , I don't think you'll be bored to exchange them ; If two equal elements are not adjacent , So even if we exchange the two in front of each other to make the two adjacent , It won't be exchanged at this time , So the order of the same elements hasn't changed , So bubble sort is a stable sort algorithm .
Time complexity :O(n^2)
Spatial complexity :O(1)
Code
public static void bubbleSort(int[] array){
for(int i=0; i< array.length-1 ;i++){
for(int j = 0; j < array.length-1-i;j++){
if(array[j] > array[j+1]){
swap(array,j,j+1);
}
}
}
}Optimize : Avoid meaningless circular judgment in an orderly situation
public static void bubbleSort2(int[] array){
for(int i=0; i< array.length-1 ;i++){
boolean flg = false ;
for(int j = 0; j < array.length-1-i;j++){
if(array[j] > array[j+1]){
swap(array,j,j+1);
flg = true;
}
}
if(!flg){
break;
}
}
}Two 、 Quick sort (Quick Sort)
introduction
Finally, our master is coming , This is listed as 20 Quick sorting, one of the top ten algorithms in the 20th century , We introduced it earlier Shell Sort amount to Directly insert the upgrade of sorting , They all belong to Insert sort class , Heap sort amount to Simply choose the upgrade of sorting , They all belong to Select sort class . and Quick sort In fact, it is the slowest one we thought before Bubble sort upgrade , They all belong to Exchange sort class . That is, it also realizes sorting through continuous comparison and mobile exchange , Just its realization , It increases the time of record comparison and movement , Move records with larger keywords directly from the front to the back , Records with smaller keywords move directly from the back to the front , Thus, the total number of comparisons and mobile exchanges are reduced
Fast sorting algorithm
The basic idea of quick sorting is : Any... In the element sequence to be sorted A particular element As At baseline , According to the sorting code, the set to be sorted Split into two subsequences , All elements in the left subsequence are less than the base value , All elements in the right subsequence are greater than the base value , Then the leftmost and rightmost subsequences repeat the process , Until all the elements are aligned in their respective positions .

Algorithm description
Fast sorting uses divide and conquer to put a string (list) It's divided into two strings (sub-lists). The specific algorithm is described as follows :
- Pick a member of the sequence , be called “ The benchmark ”(pivot);
- Reorder the sequence , All elements smaller than the base value are placed in front of the base value , All elements that are larger than the base value are placed after the base value ( The same number can go to either side ). After the partition exits , The benchmark is in the middle of the sequence . This is called a partition (partition) operation ;
- recursively (recursive) Sort the substrings of elements that are less than the base value and elements that are greater than the base value .
// Let's say that... Is sorted in ascending order array Array [left, right) Sort the elements in the interval
void QuickSort(int[] array, int left, int right)
{
if(right - left <= 1)
return;
// Align... According to the reference value array Array of [left, right) The elements in the interval are divided
int div = partion(array, left, right);
// After the division is successful, use div The left and right parts are formed for the boundary [left, div) and [div+1, right)
// Recursive row [left, div)
QuickSort(array, left, div);
// Recursive row [div+1, right)
QuickSort(array, div+1, right);
}The above is a recursive implementation of quick sorting Main frame , Discovery and Binary tree preorder traversal The rules are very much like , When writing a recursive framework, you can think about the pre order traversal rules of binary tree, which can be written quickly , In the following sequence, you only need to analyze how to divide the data in the interval according to the benchmark value .
A common way to divide an interval into left and right halves according to the reference value :
1、Hoare edition
Hoare Law is the founder of fast platoon Hoare Named , It is also the initial implementation version of fast platoon . Its basic idea is to use Two pointers Respectively point to the... Of the array to be sorted start and ending .
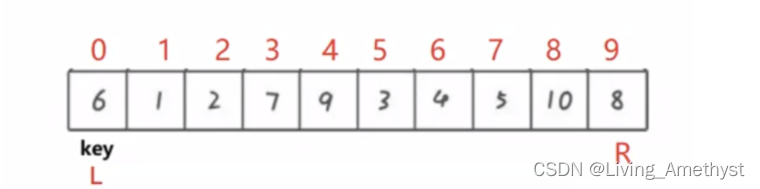
- If we take the header value as our key value , Then we must let the right pointer move first
- If we take the tail value as our key value , Then we must let the left pointer move first
Pictured , We take the header value as key value
How to move and How to find benchmark
- right Pointer until less than key The value of just stopped
- left Pointer until greater than key The value of just stopped
- take left and right Exchange the corresponding values . Repeat the above process until the two meet
- After encounter , take key The value of the subscript is exchanged with the value where it meets
- At this point, the meeting place is the benchmark
Let's use the dynamic diagram to deduce
Code :
//Hoare Law
public static int partitionHoare(int[] array,int low,int high){
int key = low;
while(low < high){
while (low < high && array[high] >= array[key]){
high--;
}
// here high Subscript is the number you are looking for
while (low < high && array[low] <= array[key]){
low++;
}
// here low Subscript is the number you are looking for
swap(array,low,high); //low and high Subscript element exchange
}
// here low and high Met
swap(array,low,key);
return low;
}
public static void quickSort(int[] array,int left,int right){
if(left >= right) return;
int pivot = partition(array,left,right);
quickSort(array,left,pivot-1);
quickSort(array,pivot+1,right);
}It should be noted that

2. Excavation method

We need to be in key Dig a hole ( hold 6 Take it out and put it in one tmp variable ), Form a pit , then R Look to the left 6 Put the small one into the pit , A new pit is formed , then L Look right , Find the ratio 6 Big , Put it into a new pit
We still use dynamic graph to deduce
The advantage of digging is that it is easier for us to understand , According to this idea, we write a fast platoon by digging a pit
// Excavation method
public static int partitionHole(int[] array,int low,int high){
int tmp = array[low];
while(low < high) {
while (low < high && array[high] >= tmp){
high--;
}
array[low] = array[high];
while (low < high && array[low] <= tmp){
low++;
}
array[high] = array[low];
}
array[low] = tmp;
return low;
}
public static void quickSort(int[] array,int left,int right){
if(left >= right) return;
int pivot = partitionHole(array,left,right);
quickSort(array,left,pivot-1);
quickSort(array,pivot+1,right);
}3、 Front and back pointer method
edition 1

seeing the name of a thing one thinks of its function , need Two pointers , One in front, one in back , Use them separately cur Indicates the front pointer ,prev Represents the back pointer , At the beginning , Our rules cur stay prev The next position of , Here we still choose the first number as the benchmark
- prev Each time, it needs to point to the last number less than the benchmark value from the left to itself
- If cur The value of is greater than the reference value , At this time, only cur++
- If cur The pointing position is smaller than the reference value
- Then we let prev++
- Judge prev++ Whether it is related to cur Equal position
- If not equal , The exchange cur and prev Value
- until cur > R after , We'll exchange prev and key, In this way, the position of the reference value is determined
Now we are still Dynamic graph deduction
Code
// Front and back pointer method 1
private static int partition(int[] array,int low,int high){
int prev = low;
int cur = low+1;
while (cur <= high){
if(array[cur] < array[low] && array[++prev]!=array[cur]){
swap(array,cur,prev);
}
cur++;
}
swap(array,prev,low);
return low;
}
public static void quickSort(int[] array,int left,int right){
if(left >= right) return;
int pivot = partition(array,left,right);
quickSort(array,left,pivot-1);
quickSort(array,pivot+1,right);
}
edition 2
This way of writing may be better understood , But the essence is the same
// Front and back pointer method 2
private static int partition2(int[] array,int low,int high){
int d = low+1;
int tmp = array[low];
for(int i = low+1;i <= high; i++){
if(array[i] < tmp){
swap(array,i,d);
d++;
}
}
swap(array,d-1,low);
return d-1;
}
public static void quickSort(int[] array,int left,int right){
if(left >= right) return;
int pivot = partition2(array,left,right);
quickSort(array,left,pivot-1);
quickSort(array,pivot+1,right);
}Optimization of quicksort
Smaller scale optimization
Every time you recurse , The data is slowly becoming orderly
When the amount of data is small and tends to be orderly , We can directly use insert sorting to optimize
public static int partitionHole(int[] array,int low,int high){
int tmp = array[low];
while(low < high) {
while (low < high && array[high] >= tmp){
high--;
}
array[low] = array[high];
while (low < high && array[low] <= tmp){
low++;
}
array[high] = array[low];
}
array[low] = tmp;
return low;
}
public static void quickSort(int[] array,int left,int right){
if(left >= right) return;
if(right-left+1 <= 10000){ // The small-scale sorting in a certain interval is directly inserted into the sorting
// Insert sort
insertSortRange(array,left,right);
return;
}
int pivot = partitionHole(array,left,right);
quickSort(array,left,pivot-1);
quickSort(array,pivot+1,right);
}
public static void insertSortRange(int[] array,int low, int end){
for(int i = low+1 ; i<=end ;i++){
int tmp = array[i];
int j = i-1;
for(; j >= low ; j--){
if(array[j] > tmp){
array[j+1] = array[j];
}else{
break;
}
}
array[j+1] = tmp;
}
}But this optimization has not been fundamentally solved In order Optimization with too deep recursion
If you want to fundamentally solve the problem , Try to make each division more uniform
Take the middle of three
We use it Take the middle of three choose key
- Take the three Numbers : head , tail , In the middle element Size centered The one of
Then exchange this element with the team head element , As key
Let's take a look at the code
public static int partitionHole(int[] array,int low,int high){
int tmp = array[low];
while(low < high) {
while (low < high && array[high] >= tmp){
high--;
}
array[low] = array[high];
while (low < high && array[low] <= tmp){
low++;
}
array[high] = array[low];
}
array[low] = tmp;
return low;
}
// Take the three Numbers , Find the first , in , Of the last three numbers Subscript of a medium-sized number
private static int medianOfThreeIndex(int[] array, int left, int right){
int mid = left + ((right-left)>>>1);
//int mid = (right+left)/2 ;
if(array[left] < array[right]){
if(array[mid] < array[left]){
return left;
}else if(array[mid] > array[right]){
return right;
}else{
return mid;
}
}else{
if(array[mid] < array[right]){
return right;
}else if(array[mid] > array[left]){
return left;
}else{
return mid;
}
}
}
public static void quickSort(int[] array,int left,int right){
if(left >= right) return;
//1. The small-scale sorting in a certain interval is directly inserted into the sorting 【 The optimization is the comparison within the interval 】
if(right-left+1 <= 10000){
// Insert sort
insertSortRange(array,left,right);
return;
}
//2. Take the middle of three 【 What is optimized is the segmentation of itself 】
int index = medianOfThreeIndex(array,left,right);
swap(array,left,index);
int pivot = partitionHole(array,left,right);
quickSort(array,left,pivot-1);
quickSort(array,pivot+1,right);
}Non recursive implementation of quick sorting
We need to use Stack
We used to be after we had determined the benchmark , Do the same operation recursively for the remaining intervals
Now let's create a stack , Put the left of the remaining interval 、 The subscripts at the right position are put into the stack respectively , As shown in the figure, a benchmark has been found 6 The situation of
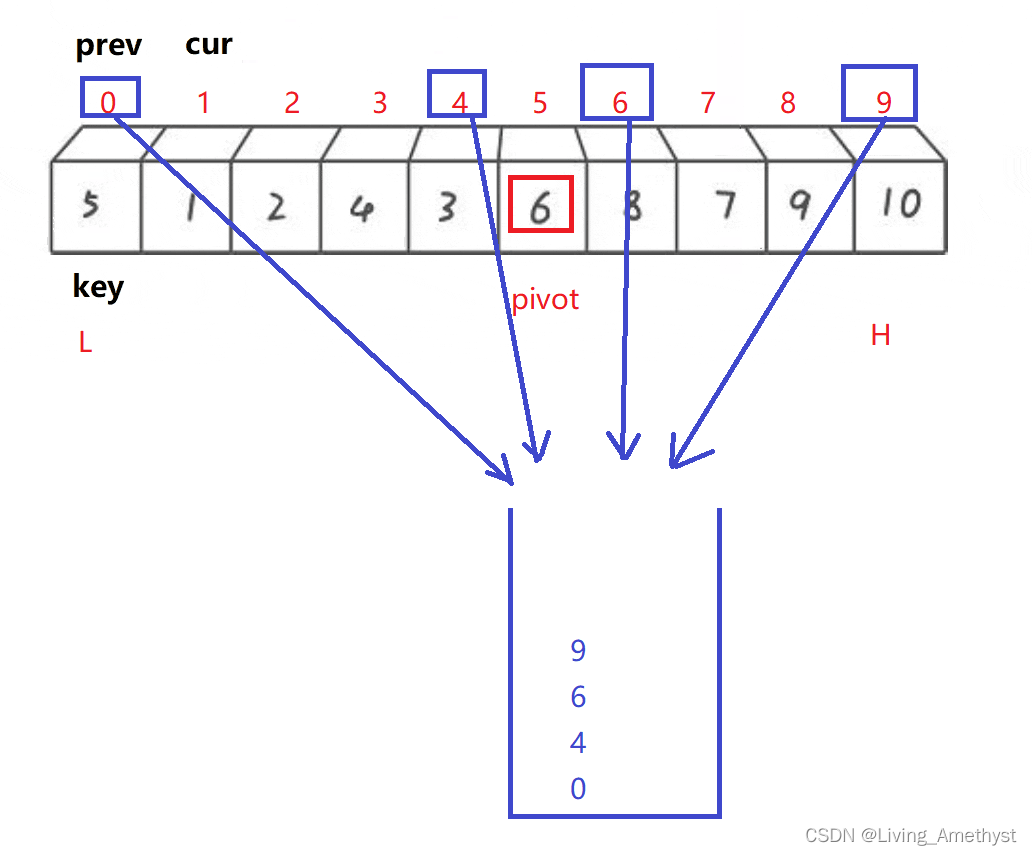
then Pop up an element at the top of the stack 9 to H, Pop up another stack top element 6 to L, According to the new L and H Find a new benchmark , Repeat the above operation
 Code
Code
// Excavation method
public static int partitionHole(int[] array,int low,int high){
int tmp = array[low];
while(low < high) {
while (low < high && array[high] >= tmp){
high--;
}
array[low] = array[high];
while (low < high && array[low] <= tmp){
low++;
}
array[high] = array[low];
}
array[low] = tmp;
return low;
}
// Quick sort ( Non recursive )
public static void quickSortNor(int[] array,int left,int right){
Stack<Integer> stack = new Stack<>();
int pivot = partitionHole(array,left,right);
if(pivot > left+1){
// Explain that there are two or more data on the left
stack.push(left);
stack.push(pivot-1);
}
if(pivot < right-1){
stack.push(pivot+1);
stack.push(right);
}
while (!stack.isEmpty()){
right = stack.pop();
left = stack.pop();
pivot = partitionHole(array,left,right);
if(pivot > left+1){
// Explain that there are two or more data on the left
stack.push(left);
stack.push(pivot-1);
}
if(pivot < right-1){
stack.push(pivot+1);
stack.push(right);
}
}
}
Quick sort summary
1. The overall performance and usage scenarios of quick sort are quite good , That's why we call it quick sort
2. Time complexity :O(N*logN)
3. Spatial complexity :O(logN)
4. stability : unstable
边栏推荐
- From 20s to 500ms, I used these three methods
- 创业团队如何落地敏捷测试,提升质量效能?丨声网开发者创业讲堂 Vol.03
- What skills does an excellent software tester need to master?
- Node - generate wechat permission verification configuration
- Some understandings of graph convolution neural network r-gcn considering relations and some explanations of DGL official code
- Kyushu cloud and Intel jointly released the smart campus private cloud framework, enabling new infrastructure for education
- Is the securities account given by qiniu business school safe? Where can I open an account
- JMeter做接口测试,如何提取登录Cookie
- Is it safe for qiniu college to open an account? How to open an account?
- New version of free mobile phone, PC, tablet, notebook four terminal Website thumbnail display diagram online one click to generate website source code
猜你喜欢
工作中非常重要的测试策略,你大概没注意过吧

export default 导出的对象,不能解构问题,和module.exports的区别

【会议资源】2022年第三届自动化科学与工程国际会议(JCASE 2022)

测试员8年工资变动,令网友羡慕不已:你一个月顶我一年工资

Picture puzzle wechat applet source code_ Support multi template production and traffic master

Leetcode skimming: binary tree 03 (post order traversal of binary tree)
Practical calculation of the whole process of operational amplifier hysteresis comparator
2022 low voltage electrician examination questions and answers
How to improve data quality

How to type spaces in latex
随机推荐
Common loss function of deep learning
gradle
Practical calculation of the whole process of operational amplifier hysteresis comparator
Leetcode question brushing: stack and queue 07 (maximum value of sliding window)
Leetcode skimming: stack and queue 06 (top k high-frequency elements)
使用多线程Callable查询oracle数据库
【mysql 07】GPG key retrieval failed: “Couldn‘t open file /etc/pki/rpm-gpg/RPM-GPG-KEY-mysql-2022“
Node - generate wechat permission verification configuration
JS -- image to base code, base to file object
RFID让固定资产盘点更快更准
449 original code, complement code, inverse code
Bc35 & bc95 onenet mqtt (old)
SQL Server 安装指南
SQL Server 安裝指南
Slf4j print abnormal stack information
Export default the exported object cannot be deconstructed, and module Differences between exports
Comprehensive usage and case questions of sub query of SQL data analysis [patient sorting]
Window sorting functions rank and deny for SQL data analysis_ rank、raw_ Number and lag, lead window offset function [usage sorting]
[bottom pop-up selector] uniapp picker component - scroll selector popped up at the bottom
Node——添加压缩文件