当前位置:网站首页>MCS:连续随机变量——LogNormal分布
MCS:连续随机变量——LogNormal分布
2022-06-23 03:56:00 【今晚打佬虎】
Lognormal
对数正态分布与正态分布变量的关系如下: x x x:对数正态变量, y y y正态变量。
y = l n ( x ) y = ln(x) y=ln(x)
x = e y x = e^y x=ey
变量 y y y是正态变量,其均值和方差记为: μ y , σ y 2 \mu_y,\sigma_y^2 μy,σy2,对数正态变量 x x x的均值和方差记为: μ x , σ x 2 \mu_x,\sigma_x^2 μx,σx2,符号表示为:
x ∼ L N ( μ y , σ y 2 ) x \sim LN(\mu_y, \sigma_y^2) x∼LN(μy,σy2)
y ∼ N ( μ y , σ y 2 ) y \sim N(\mu_y, \sigma_y^2) y∼N(μy,σy2)
注意:变量 x x x的参数是变量 y y y的均值和方差,变量 x , y x, y x,y参数之间的关系如下:
μ x = e x p [ μ y + σ y 2 / 2 ] \mu_x = exp \Big[\mu_y + \sigma_y^2/2 \Big] μx=exp[μy+σy2/2]
σ x 2 = e x p [ 2 μ y + σ y 2 ] [ e x p ( σ y 2 ) − 1 ] \sigma_x^2 = exp \Big[2\mu_y + \sigma_y^2 \Big] \Big[exp(\sigma_y^2) - 1 \Big] σx2=exp[2μy+σy2][exp(σy2)−1]
μ y = l n [ μ x 2 / μ x 2 + σ x 2 ] \mu_y = ln \Big[\mu_x^2 / \sqrt{\mu_x^2 + \sigma_x^2} \Big] μy=ln[μx2/μx2+σx2]
σ y 2 = l n [ 1 + σ x 2 / μ x 2 ] \sigma_y^2 = ln \Big[1 + \sigma_x^2 / \mu_x^2 \Big] σy2=ln[1+σx2/μx2]
生成参数为 μ y , σ y 2 \mu_y,\sigma_y^2 μy,σy2的随机的对数正态变量 x x x:
- Generate a random standard normal variate, z z z
- A random normal variate becomes : y = μ y + z × σ y y = \mu_y + z \times \sigma_y y=μy+z×σy
- The random lognormal variate is x = e y x = e^y x=ey
- Return x.
例:设 x x x是一个对数正态变量,其均值和方差为: μ x = 10 , σ x 2 = 400 \mu_x = 10,\sigma_x^2 = 400 μx=10,σx2=400,满足这个条件的随机对数正态变量计算过程如下:
- 计算出正态变量 y y y的均值和方差:
μ y = l n [ μ x 2 / μ x 2 + σ x 2 ] = 1.498 \mu_y = ln \Big[\mu_x^2 / \sqrt{\mu_x^2 + \sigma_x^2} \Big] = 1.498 μy=ln[μx2/μx2+σx2]=1.498
σ y 2 = l n [ 1 + σ x 2 / μ x 2 ] = 1.609 \sigma_y^2 = ln \Big[1 + \sigma_x^2 / \mu_x^2 \Big] = 1.609 σy2=ln[1+σx2/μx2]=1.609
σ y = 1.269 \sigma_y = 1.269 σy=1.269
- 生成一个标准的随机正态变量N(0, 1), z = 1.37 z = 1.37 z=1.37
- 根据标准正态变量计算得到随机正态变量: y = μ y + z × σ y = 1.498 + 1.37 × 1.269 = 3.236 y = \mu_y + z \times \sigma_y = 1.498 + 1.37 \times 1.269 = 3.236 y=μy+z×σy=1.498+1.37×1.269=3.236
- 随机对数正态变量: x = e y = e 3.236 = 25.44 x = e^y = e^{3.236} = 25.44 x=ey=e3.236=25.44
- x = 25.44 x = 25.44 x=25.44
生成对数正态分布变量
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
def generate_normal_var(mean=0, std=1, method=2):
if method == 2:
sum_u = np.random.uniform(0, 1, (12,)).sum()
z = -6.0 + sum_u
else:
u1 = np.random.uniform(0, 1)
u2 = np.random.uniform(0, 1)
z = np.sqrt(-2 * np.log(u1)) * np.cos(2 * np.pi * u2)
if mean == 0 and std == 1:
return z
else:
return mean + z * std
def generate_lognormal_var(mean=0, variance=1, n=10000):
mu_y = np.log(mean*mean / np.sqrt(mean * mean + variance))
sigma_y = np.log(1 + variance/(mean * mean))
std_y = np.sqrt(sigma_y)
x = [np.exp(generate_normal_var(mu_y, std_y)) for i in range(n)]
return x
ln_x = generate_lognormal_var(1, 0.25)

边栏推荐
猜你喜欢

What is the average annual salary of an outsourced tester who has worked for 5-8 years?
onnxoptimizer、onnxsim使用记录
搭建一套 gocd 的环境

Ams:startactivity desktop launch application

UI automation positioning edge -xpath actual combat
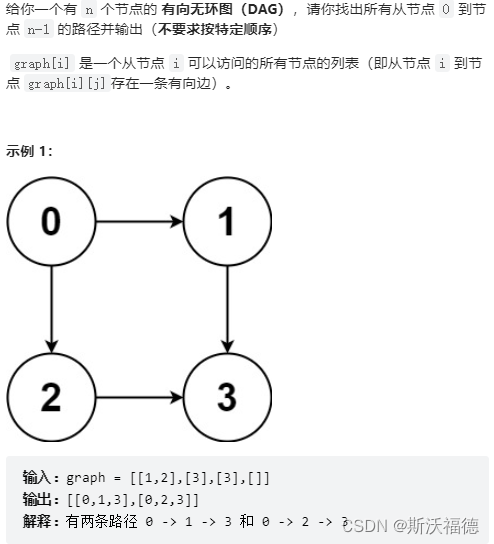
LeetCode 797:所有可能的路径

渗透测试基础 | 附带测试点、测试场景

985 test engineer is hanged. Who is more important in terms of education and experience?

网上有真实的兼职吗?大学生怎么找暑期兼职?

九九乘法表.bat
随机推荐
Swiftui 2.0 course notes Chapter 5
APP自动化测试-Appium进阶
李宏毅《机器学习》丨5. Tips for neural network design(神经网络设计技巧)
STP总结
【Leetcode】最长递增子序列问题及应用
MySQl基础
Sift特征点提取
Open source ecology 𞓜 super practical open source license basic knowledge literacy post (Part 2)
C'est dur de trouver un emploi? Ali des trois côtés, heureusement qu'il s'est bien préparé et qu'il a pris un produit.
Laravel8 implementation of picture verification code
shutdown关机命令
UI automation positioning edge -xpath actual combat
Zygote process
【opencv450】 图像相减、二值化、阈值分割
The propeller framework v2.3 releases the highly reusable operator library Phi! Restructure development paradigm to reduce cost and increase efficiency
Swiftui 2.0 course notes Chapter 4
图片降噪DeNoise AI
软件项目管理 8.4.软件项目质量计划
[laravel series 7.8] broadcasting system
In unity, how to read and write a scriptableobject object in editor and runtime