Pattern recognition - 1 Bayesian decision theory_ P1

Knowledge structure (P1+P2)

1. Summary
2. Minimum error rate Bayesian decision
3. Minimum risk Bayesian decision
4. Classifier design
5. The discriminant function under Gaussian density

1.1 Summary

Prior probability ： Probability based on experience or previous data analysis .
Posterior probability ： The probability that the data will be corrected again .
Probability density function ： Describe the output value of random variables , A function of the probability of being near a certain value . The probability that the value of a random variable falls within a certain region is the integral of the probability density function in this region . When the probability density function exists , Cumulative distribution function It's the integral of the probability density function . Probability density functions are generally marked in lowercase .
Class conditional probability density function ： Assume x It's a continuous random variable , Its distribution depends on the category status p(x|ω). That is, the category status is ω At the time of the x The probability density function of .
The feature space ： Eigenvector Situated d Viogerid space , Write it down as .

Bayesian decision theory The starting point of this paper is to make use of the quantitative tradeoff between the decision-making of different classifications of probability and the decision-making cost of response . It makes the following assumptions ： That is, the decision problem can be described in the form of probability , And assume that all relevant probability structures are known .
Loss function ：, Indicates when the category is The decision taken The loss caused , Short for .
Discriminant function ： Some functions used to express decision rules . A set of discriminant functions is usually defined 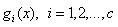Used to represent multi class decision rules . If To any All set up , Will belong to class . Refer to Bayesian decision rules , A series of discriminant functions can be defined ：

Decision making ： about c Class classification problem , According to the decision rules, we can put d Dimensional feature space is divided into c Decision making areas , The boundary of the decision area is the decision surface . These decision surfaces are Hypersurfaces in feature space , Obviously, two adjacent decision-making surfaces , The value of its discriminant function is equal . namely , If and adjacent , Then their decision surface equations satisfy .
Equal density trajectory ： In the discriminant function under Gaussian density , The equal density trajectory is a super ellipsoid （ The direction of its principal axis is determined by the eigenvector of the matrix , The length of the principal axis is proportional to its eigenvalue ）. From the multivariate normal distribution, we can know , When its exponential term is equal to a constant , density p(x) The value of does not change , Therefore, the equifunction points are points of constants obtained by using the following equation , namely ：

covariance ： Used to measure the overall error of two variables , The expectation of making the overall error of two variables , For example, for two random variables X and Y The covariance between is recorded as Cov(X,Y).
Covariance matrix ： It is the generalization of two random variables to high-dimensional random vectors . set up by n Dimensional random variable , It's called matrix by n Dimensional random variable X The covariance matrix of , Write it down as D(X), among 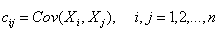by X Components of 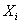and The covariance .
Markov distance ： sample x To center μ The calculation of follows the following formula ：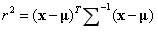

Euclidean distance ：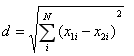

1.2 Minimum error rate decision

Problem description ：
To a c Class problem 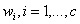, Eigenvectors , A priori probability is known And conditional probability density function . Its task is to measure the observed samples , Choose which category is the most reasonable （ Minimum error rate ）？

Bayesian decision making ：
Posterior probability ：

Decision making rules ：

Error rate ：

Minimum error rate ：

Several equivalent forms of Bayesian decision making ：

1.3 Minimum risk decision

In practical application scenarios , It is not enough to minimize the error rate of decision making , We should also consider the risks arising from the judgment . So the concept of loss is introduced , When considering the loss caused by misjudgment , Not just based on the size of a posteriori probability , It is necessary to consider whether the decision taken has the least loss . For a given x, Consider making a decision about it , but The specific category status is unknown , Therefore, conditional risk should be considered .

Problem description ： Yes c Class problem ,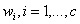, Eigenvectors , A priori probability is known , Conditional probability density function , The decision space contains a A decision , And the loss function . Its task is ： If a sample is observed , Which category should they be classified into to minimize the risk ？

Conditional risk and expected risk ：
Conditional risk ：, It's a random variable Function of , It can be calculated as follows :

Expected risk 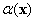：, Treat decision rules as random variables Function of . For all possible samples in the feature space The expected loss from the decision taken is ：

Minimum risk Bayesian decision is to minimize the expected risk .

computational procedure ：

• Using Bayes formula to calculate posterior probability ：
  
• Use decisions to calculate risk ：
  
• Choose the decision with the least risk among various decisions ：
  

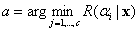
There are two kinds of situations ： For two cases , There is no rejection （a=c=2）, Yes ：

The decision rule is ：

namely ：

Other equivalent forms ： No loss of generality , It can be assumed , Therefore, the decision rule can also be expressed as ：

and

0-1 loss： In the classification problem , Usually each category state is associated with c Class about , And decision It is usually interpreted as a category status , Be adjudicated as . If a decision is taken The actual category is , So in i=j The criterion is correct , Otherwise, misjudgment will occur . Avoid misjudgment , It is necessary to find a rule to make the probability of misjudgment （ Error rate ） To minimize the . The loss function in this case is “0-1 Loss ”, Also known as “ Symmetry loss ” function ：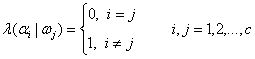

The risk corresponding to this loss function is the average error probability , Because the conditional risk is ：

Minimize the average error rate （MAP）：
Yes, give i≠j, If , It's called .

1.4 classifier

Classifier design ： The classifier can be seen as calculating c A discriminant function , A machine that selects the class corresponding to the maximum value of the discriminant function as the classification result .

The discriminant function in two cases ：
For two cases , Just define a discriminant function ：

The decision surface equation in two cases ：g(x)=0. When x When it is one dimension , The decision surface is a point ; When x When it is two-dimensional , The decision surface is a line ; In three dimensions , The decision-making side is one side , The higher dimension is a hypersurface .

Classification error rate ：
Talk about error probability and error integral , Note that this knowledge point should have been placed after the discriminant function of normal distribution , But because of the typesetting problem, I put it here first .

• Average misclassification probability in two cases ：
  
• Average misclassification probability in multi class cases ：
  
• The average classification accuracy in multi class case ：
  

Summary

• In fact, it's easy to know some conceptual formulas , But it takes a lot of effort to deeply understand and skillfully use . The understanding of Bayesian decision theory is based on Conditional probability 、 Understanding of full probability formula and Bayes formula . As for the normal distribution discriminant function, you need to have a solid and comprehensive understanding of the normal distribution and its related properties .
• This chapter basically revolves around There are two kinds of situations an .
• MD The formula editor is hard to use .
• In this chapter, you need to master some “ distance ” The concept of , About distance （ Euclidean distance 、 Min's distance 、 Markov distance 、 Manhattan distance 、 Cosine distance 、 Hamming distance, etc ） See the column ：[ Address ]