2022暑假牛客多校1 (A/G/D/I)

A.Villages: Landlines

区间问题的板子

#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
#define ll long long
#define pll pair<ll, ll>
vector<pll> v;

int main()
{
    
    ll n;
    cin >> n;
    ll xs, rs;
    cin >> xs >> rs;
    for (ll i = 1; i < n; ++i)
    {
    
        ll X, R;
        cin >> X >> R;
        v.push_back({
    X - R, R + X});
    }
    v.push_back({
    xs - rs, xs + rs});
    sort(v.begin(), v.end());
    ll ans = 0;
    ll L = v[0].first, r = v[0].second;
    for (int i = 1; i < n; ++i)
    {
    
        if (v[i].first > r)
        {
    
            ans += v[i].first - r;
            L = v[i].first;
            r = v[i].second;
        }
        else
        {
    
            r = max(v[i].second, r);
        }
    }
    cout << ans;
    return 0;
}

板子
acwing上有详细的问题及解答
	sort(p, p + m, cmp);
	int ans = 0;
	int L = p[0].first, r = p[0].second;
	for (int i = 1; i < m; ++i) {
    
		if (p[i].first > r) {
    
			ans += r - L + 1;
			L = p[i].first;
			r = p[i].second;
		} else {
    
			r = max(p[i].second, r);
		}
	}
	ans += r - L + 1;		
	cout << l + 1 - ans<< endl;

G. Lexicographical Maximum

#include <cstdio>
#include<iostream>
using namespace std;
int main()
{
    
    char c;
    bool flag = false, mark = false;
    unsigned long long cnt = 0, num = 1;
    char pre;
    scanf("%c", &c);
    pre = c;
    if (c != '9')
        mark = true;
    else
        ++cnt;
    
    while (scanf("%c", &c))
    {
    
        if(! (c >= '0' && c <= '9')) break;
        printf("9");
        flag = true;
        if (c != '9')
            mark = true;
        else
            ++cnt;
        ++num;
        pre = c;
    }
    if (!flag || (cnt == num - 1 && pre != '9')){
    
       printf("%c", pre);
    }
    else if (flag && !mark)
         printf("9");
    return 0;
}

D. Mocha and Railgun

几个结论：

• 弦长和弧长无直接关系
• 求∝：反三角函数（atan精确度最高）
• sin(∝/2) = L / 2*R
• 弧长：∝ * Π * R / 180 或者求弧长积分或者 ∝ * r
• 弦长相同时,半径越长,弧长越短;反之亦然。 弧长相同时,半径越长,弦长越长;反之亦然
• 旋转的线段所在的直线过圆心时，圆弧上的曲率(角度)最大；相同长度上的圆弧，曲率越大，圆弧越
  方法一：
  由于公式 ∝ * r，可得角度越大弧长越大；
  使角度最大的方法就是让AB的延长线过原点
  当结论记吧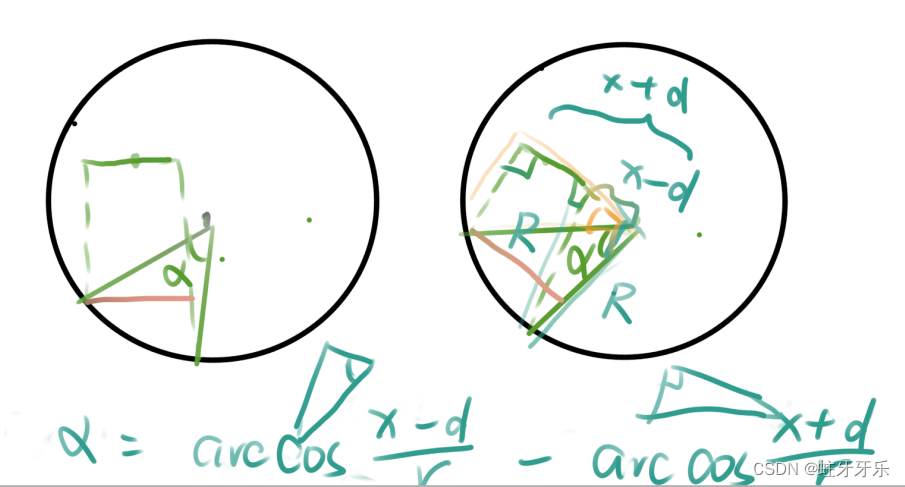
  

int main(){
    
    int t;
    cin >> t;
    while(t--){
    
        double r, x, y, d;
        cin >> r >> x >> y >> d;
        double D = sqrt(x * x + y * y);//到原点的距离
        double a = acos((D - d) / r) - acos((D + d) / r);//角度3-角度1
        double res = a * r;
        printf("%.12f\n", res);
    }
    return 0;
}

方法二：
求导，不会

I.Chiitoitsu

期望dp
本题需要取模，而期望值并不一定是整数，所以要用到逆元（分数）和快速幂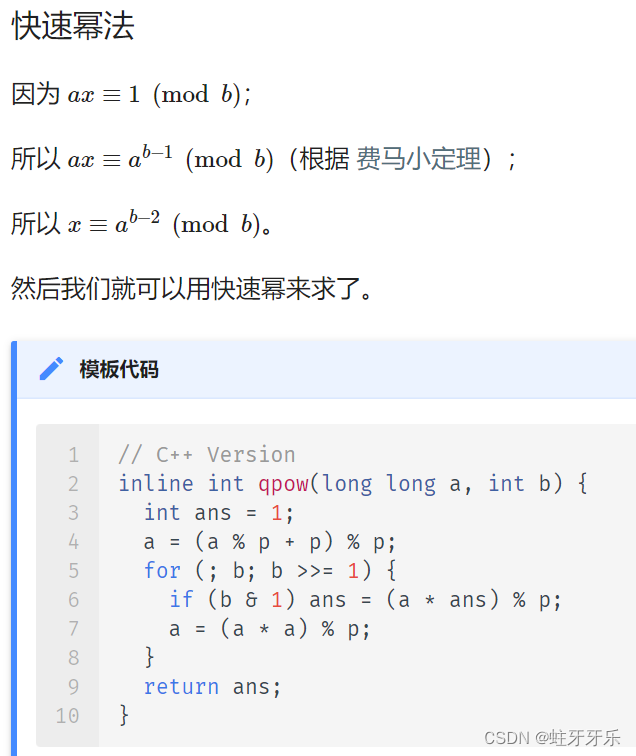

来源 oi-wiki

总结：

• 一般多组数据的dp，极有可能就是提前打表
• 当需要对分数取模时，用逆元快速幂

参考
1.
2.
3.

ll fast_power(ll a, ll b)
{
    
    ll pr = 1;
    while (b > 0)
    {
    
        if (b & 1)
            pr = pr * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return pr;
}
ll dp[15][140];
ll f[140][15];
void init()
{
    
    //需要预处理 利用最基本的方法
    // for(int i = 3;i <= 123;i ++){
    
    // dp[1][i] = (1 + (((i - 3) * fast_power(i,p - 2) % p) * dp[1][i-1] % p)) % p;
    // }
    // for(ll i = 3;i <= 13;i += 2){
    
    // for(ll j = 3;j <= 123;j ++){
    
    // dp[i][j] = (1 + (((i * 3) * fast_power(j,p - 2) % p) * dp[i - 2][j - 1] % p) + (((j - i * 3) * fast_power(j,p - 2) % p) * dp[i][j - 1] % p)) % p;
    // }
    // }
    //不需要预处理 利用2*j-1
    for (int i = 3; i <= 123; i++)
    {
                                      
        int inv = fast_power(i, p - 2); 
        for (int j = 1; j <= 7 && 3 * (2 * j - 1) <= i; j++)
        {
    
            f[i][j] = 3ll * (2 * j - 1) * inv % p * (f[i - 1][j - 1] + 1) % p;
            f[i][j] = (f[i][j] + 1ll * (i - 3 * (2 * j - 1)) * inv % p * (f[i - 1][j] + 1) % p) % p;
        }
    }
}
map<string, int> mp;
int main(){
    
    init();
    int t;
    cin >> t;
    for (int q = 1; q <= t; ++q)
    {
    
        mp.clear();
        string s;
        cin >> s;
        // int num = 0;
        // for(int i = 0; i < 26; i += 2){
    
        // string temp = "";
        // temp += s[i];
        // temp += s[i + 1];
        // ++mp[temp];
        // }
        // for(int i = 0; i < 26; i += 2){
    
        // string temp = "";
        // temp += s[i];
        // temp += s[i + 1];
        // if(mp[temp] == 1)
        // ++num;
        // }
        int num = 7;
        for (int i = 0; i < 26; i += 2)
        {
    
            string temp = "";//int可能会冲突
            temp += s[i];
            temp += s[i + 1];
            ++mp[temp];
            if (mp[temp] == 2)
                --num;
        }
        printf("Case #%d: %lld\n", q, f[123][num]); // dp[num][123]
    }
    return 0;
}

最短路 + 期望dp: P1850 [NOIP2016 提高组] 换教室

int c[2010], d[2010];
double k[2010];
int g[310][310];
double dp[2010][2010][2];
int main() {
    
	IOS;
    int n, m, v, e;
    cin >> n >> m >> v >> e;
    //时间段数量 最多申请 教室数量 道路数量
    for (int i = 1; i <= n; ++i){
    
        cin >> c[i];//被安排上课的的教室
    }
     for (int i = 1; i <= n; ++i){
    
        cin >> d[i];//另一间上同样课程的教室（同样时间）
    }
     for (int i = 1; i <= n; ++i){
    
        cin >> k[i];//换第i个教室的概率
    }
    remax(g);
    for (int i = 0; i < e; ++i)
    {
    
        int a, b,c;
        cin >> a >> b >> c;
        c = min(g[a][b], c);
        g[a][b] = g[b][a] = c;
    }
    for (int k = 1; k <= 300; ++k){
    
        for (int i = 1; i <= 300; ++i){
    
            for(int j = 1; j <= i; ++j){
    
                if(g[i][k] + g[k][j] < g[i][j])
                    g[i][j] = g[j][i] = g[i][k] + g[k][j];
            }
        }
        g[k][k] = 0;
    }
    for (int i = 0; i <= n; i++)
        for (int j = 0; j <= m; j++){
    
            dp[i][j][0] = dp[i][j][1] = 0x3f3f3f3f;
        }
    
    dp[1][0][0] = dp[1][1][1] = 0;
    for (int i = 2; i <= n; ++i){
    
        dp[i][0][0] = dp[i - 1][0][0] + g[c[i - 1]][c[i]];
        for (int j = 1; j <= min(n, m); ++j){
    
            double temp = dp[i - 1][j][1] + g[c[i - 1]][c[i]] * (1 - k[i - 1]) + g[d[i - 1]][c[i]] * k[i - 1];
            dp[i][j][0] = min(dp[i][j][0], min(dp[i - 1][j][0] + g[c[i - 1]][c[i]], temp));
            temp = dp[i - 1][j - 1][1] + g[c[i - 1]][c[i]] * (1 - k[i - 1]) * (1 - k[i]) + g[c[i - 1]][d[i]] * (1 - k[i - 1]) * k[i] + g[d[i - 1]][c[i]] * k[i - 1] * (1 - k[i]) + g[d[i - 1]][d[i]] * k[i - 1] * k[i];
            dp[i][j][1] = min(dp[i][j][1], min(dp[i - 1][j - 1][0] + g[c[i - 1]][c[i]] * (1 - k[i]) + g[c[i - 1]][d[i]] * k[i], temp));
        }
    }
    double ans = 0x3f3f3f3f;
    for (int i = 0; i <= m; ++i){
    
        ans = min(ans, min(dp[n][i][0], dp[n][i][1]));
    }
    printf("%.2f", ans);
    return 0;
}

经验：不能直接remax(dp)，会出现非常小的数导致出错，应该双重for赋0x3f3f3f3f