当前位置:网站首页>Niu Ke's questions -- binary search tree and bidirectional linked list
Niu Ke's questions -- binary search tree and bidirectional linked list
2022-06-11 18:28:00 【HHYX.】
Binary search tree and double linked list
Topic link : Binary search tree and double linked list
Title Description
Enter a binary search tree , The binary search tree is transformed into a sorted double linked list . As shown in the figure below 
Data range : Enter the number of nodes of the binary tree 0 \le n \le 10000≤n≤1000, The value of each node in the binary tree 0\le val \le 10000≤val≤1000
requirement : Spatial complexity O(1)O(1)( That is, operate on the original tree ), Time complexity O(n)O(n)
Be careful :
1. It is required that no new nodes can be created , You can only adjust the direction of the node pointer in the tree . When the conversion is complete , The left pointer of the node in the tree needs to point to the precursor , The right pointer of the node in the tree needs to point to the successor
2. Returns the pointer of the first node in the linked list
3. Function return TreeNode, There are left and right pointers , In fact, it can be regarded as a data structure of a two-way linked list
4. You don't have to output a two-way linked list , The program will automatically print out according to your return value
Input description :
The root node of a binary tree
Return value description :
One of the head nodes of the two-way linked list .
Topic analysis
The problem is to change a binary search tree structure into a two-way linked list , The left pointer points to the front drive , Right pointer to successor . At the same time, the two-way linked list is required to be orderly . One of the characteristics of binary search tree is that if you traverse the binary search tree in middle order, you can get an orderly arrangement . You must modify the original tree and cannot create new nodes . So how to modify it . According to the characteristics of middle order traversal , You can set a prev The pointer , Start set to empty , In fact, it is the precursor node of each node , In this way, during the middle order traversal , The linked list can be connected before and after , In this way, the bidirectional linked list required in the title can be realized . Finally, according to the requirements of the topic , Return the head node of the linked list . The code implementation is as follows :
cur->left = prev;
if (prev)
{
prev->right = cur;
}
prev = cur;
Code implementation
void InOrder(TreeNode* cur, TreeNode*& prev)// In the sequence traversal
{
if (cur == nullptr)// If it is empty, it will return to
{
return;
}
InOrder(cur->left, prev);
cur->left = prev;
if (prev)
{
prev->right = cur;
}
prev = cur;
InOrder(cur->right, prev);
}
TreeNode* Convert(TreeNode* pRootOfTree)
{
if (pRootOfTree == nullptr)
{
return nullptr;
}
TreeNode* prev = nullptr;
TreeNode* cur = pRootOfTree;
InOrder(cur, prev);
TreeNode* ret = pRootOfTree;
while (ret->left)
{
ret = ret->left;
}
return ret;
}

边栏推荐
猜你喜欢

求字符串中最大的 3 位相同数字

SISO decoder for a general (n, n-1) SPC code (supplementary Chapter 3)

RadioGroup动态添加RadioButton

全志T3开发板(4核ARM Cortex-A7)——系统启动阶段LOGO显示详解

Several commands related to domain name

map和set
![[Golang]力扣Leetcode - 349. 两个数组的交集(哈希表)](/img/92/03de54c9f08eae5bc920b04d2b8493.png)
[Golang]力扣Leetcode - 349. 两个数组的交集(哈希表)
![[c language] shift elements after sorting elements of an array](/img/5b/3e74fc40787d94f6d0ab93332140ba.png)
[c language] shift elements after sorting elements of an array

信号的处理与捕捉
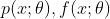
神经网络与深度学习-2- 机器学习简单示例-PyTorch
随机推荐
EditText 金额限制
Is it good or not to open a stock account on the flush? Is it safe?
[golang] leetcode - 349 Intersection of two arrays (hash table)
Introduction to social engineering practice
Cryptology Summary
Getting started with CTF
【新手上路常见问答】关于项目管理
. Net core redis hyperloglog type
力扣刷题——二叉树的层序遍历Ⅱ
SISO decoder for a general (n,n-1) SPC code(補充章節3)
MMA-Self-defining function
[golang] leetcode - 292 Nim games (Mathematics)
[c language] shift elements after sorting elements of an array
vim常用命令
“LSTM之父”新作:一种新方法,迈向自我修正的神经网络
MMA-Self-defining function
[c language] output the students within the specified score range with the structure
单选按钮 文字背景同时改变
* Jetpack 笔记 LifeCycle ViewModel 与LiveData的了解
牛客刷题——part7