当前位置：网站首页>FPGA（七）RTL代码之三（复杂电路设计2）

FPGA（七）RTL代码之三（复杂电路设计2）

2022-06-29 03:04:00 【简宸~】

系列文章目录

FPGA（五）RTL代码之一（跨时钟域设计）
FPGA（六）RTL代码之二（复杂电路设计1）

文章目录

前言

这不马上要面试了嘛，有些慌！HDLbits的题目已经刷完了，但又知道自己还远远不够，就从一个B站UP主那里截取了一个刷题的题库，只有题目，代码都要自己去写，所以写的代码可能存在问题，我打算分成好几节把刷的题目代码放出来。仅供自己学习。如果有需要的也可以看看，若有错误，还望指出！谢谢！
请添加图片描述

一、线性反馈移位寄存器LFSR

LFSR的基础原理：（九）详解线性反馈移位寄存器（LFSR）
Verilog的LFSR参考：Verilog设计实例（1）线性反馈移位寄存器（LFSR）
LFSR(线性反馈移位寄存器)

线性反馈移位寄存器（Linear Feedback Shift Register，LFSR）。

小小总结一下：
LFSR它是一种在FPGA内部有用的设计。 LFSR易于合成，这意味着它们占用的资源相对较少，并且可以在FPGA内部以很高的时钟速率运行。

首先它是在一个移位寄存器的基础上，增加反馈函数，这个反馈函数在FPGA内部是事先有所定义的。输出是从最高位逐步移位输出，成为一个序列；根据反馈函数，计算出的值增加到这个移位寄存器的最低位。LFSR是有周期的，即输出了多少个数字之后，又进入下一轮，输出一模一样的一轮"0"“1”。

二、Wallace树型乘法器

学习文章：【HDL系列】乘法器(4)——图解Wallace树

小小总结一下：
感觉就是全加器，和与进位分开计算——每3个加数分为一组，压缩至2个加数，即压缩的两个加数，一个是和，一个是进位。为啥要这么做？降低门延迟！

设计一个8*8 Wallace树型阵列乘法器，把代码放在这里，免得再去下载了：
①全加器

module full_adder(
    input a,
    input b,
    input cin,
    output cout,	//进位
    output s		//和
);

assign s = a ^ b ^ cin;
assign cout = a & b | (cin & (a ^ b));
//等价于
//assign {cout,s} = a + b + cin;
endmodule

②CSA加法器

module csa #(width=16) (
	input [width-1:0] op1,
	input [width-1:0] op2,
	input [width-1:0] op3,
	output [width-1:0] S,
	output [width-1:0] C
);
genvar i;
generate
	for(i=0; i<width; i++) begin
		full_adder u_full_adder(
			.a      (   op1[i]    ),
			.b      (   op2[i]    ),
			.cin    (   op3[i]    ),
			.cout   (   C[i]	  ),
			.s      (   S[i]      )
		);
	end
endgenerate
endmodule

③RCA加法器

module rca #(width=16) (
    input  [width-1:0] op1,
    input  [width-1:0] op2,
    input  cin,
    output [width-1:0] sum,
    output cout
);

wire [width:0] temp;
assign temp[0] = cin;
assign cout = temp[width];

genvar i;
for( i=0; i<width; i=i+1) begin
    full_adder u_full_adder(
        .a      (   op1[i]     ),
        .b      (   op2[i]     ),
        .cin    (   temp[i]    ),
        .cout   (   temp[i+1]  ),
        .s      (   sum[i]     )
    );
end
endmodule

④顶层文件

module wallace_mul #(width=8) (
	input [width-1:0] X,
	input [width-1:0] Y,
	output [2*width-1:0] P
);

wire [width-1:0][2*width-1:0] xy;
wire [width*2-1:0] s_lev01;
wire [width*2-1:0] c_lev01;
wire [width*2-1:0] s_lev02;
wire [width*2-1:0] c_lev02;
wire [width*2-1:0] s_lev11;
wire [width*2-1:0] c_lev11;
wire [width*2-1:0] s_lev12;
wire [width*2-1:0] c_lev12;
wire [width*2-1:0] s_lev21;
wire [width*2-1:0] c_lev21;
wire [width*2-1:0] s_lev31;
wire [width*2-1:0] c_lev31;

genvar i;
genvar j;

//generate xy
generate 
    for(i=0; i<width; i++) begin
        for(j=0; j< width; j++) begin
            assign xy[i][j] = Y[i] & X[j];
        end
        assign xy[i][2*width-1 : width] = 8'd0; //for "X"
    end
endgenerate

//level 0
csa #(width*2) csa_lev01(
	.op1( xy[0] ),
	.op2( xy[1] << 1 ),
	.op3( xy[2] << 2 ),
	.S	( s_lev01),
	.C	( c_lev01)
);

csa #(width*2) csa_lev02(
	.op1( xy[3] << 3),
	.op2( xy[4] << 4),
	.op3( xy[5] << 5),
	.S	( s_lev02 ),
	.C	( c_lev02 )
);

//level 1
csa #(width*2) csa_lev11(
	.op1( s_lev01 ),
	.op2( c_lev01 << 1 ),
	.op3( s_lev02 ),
	.S	( s_lev11 ),
	.C	( c_lev11 )
);

csa #(width*2) csa_lev12(
	.op1( c_lev02 << 1 ),
	.op2( xy[6] << 6 ),
	.op3( xy[7] << 7 ),
	.S	( s_lev12 ),
	.C	( c_lev12 )
);

//level 2
csa #(width*2) csa_lev21(
	.op1( s_lev11 ),
	.op2( c_lev11 << 1 ),
	.op3( s_lev12 ),
	.S	( s_lev21 ),
	.C	( c_lev21 )
);

//level 3
csa #(width*2) csa_lev31(
	.op1( s_lev21 ),
	.op2( c_lev21 << 1 ),
	.op3( c_lev12 << 1 ),
	.S	( s_lev31),
	.C	( c_lev31)
);

//adder
rca #(2*width) u_rca (
    .op1 ( s_lev31  ), 
    .op2 ( c_lev31 << 1  ),
    .cin ( 1'b0   ),
    .sum ( P      ),
    .cout(        )
);
endmodule

三、Booth乘法器

基础入门学习：八位“Booth二位乘算法”乘法器
关于补码概念：补码的计算方法

这篇文章已经讲的很详细了，我也就不赘述了，如果后面有时间的话再来尝试着写一下一位和四位的程序。

小小总结一下booth乘法器：
当被乘数 A A A乘以乘数 B B B时，直接用补码相乘，即 A 补 ∗ B 补 A_补*B_补 A补​∗B补​，在二进制计算过程中，乘数补码 B 补 = y n − 1 y n − 2 y n − 3 . . . y 2 y 1 y 0 y − 1 B_补=y_{n-1}y_{n-2}y_{n-3}...y_2y_1y_0y_{-1} B补​=yn−1​yn−2​yn−3​...y2​y1​y0​y−1​,这个时候就要用到一点规则了：
一位乘：

y i − 1 − y i y_{i-1}-y_i yi−1​−yi​符号为正或无符号，取加；符号为负，取减

举例如下，以(-6)x(-7)为例，补码乘是1010x1001，列出竖式：
在这里插入图片描述
二位乘：

y i − 1 + y i − 2 ∗ y i + 1 y_{i-1}+y_i-2*y_{i+1} yi−1​+yi​−2∗yi+1​符号为正或无符号，取加；符号为负，取减

举例如下，以(-6)x(-7)为例，补码乘是1010x1001，列出竖式：
在这里插入图片描述

四、4位超前进位加法器

Verilog——串行四位加法器和超前四位加法器74HC283
参照上面的文章，就可以知道原理。
但是上面的代码输入应该是 A , B A,B A,B,所以改了一下：

1. RTL代码

  //filename:ahead_gene_circuit.v
module ahead_gene_circuit(
  input [3:0]     A,B ,
  input           C01 ,
  output  [3:0]   C   ,
  output reg[3:0] S
);
/*参数说明： 输入： P,G为定义的中间变量，产生变量Gi，传输变量Pi Ci为来自低位的进位 输出： C为各位的进位信号 S为进位加法的和 */
//根据各位进位信号的逻辑表达式，进行数据流建模。
wire  [3:0] P,G;
assign G = A & B;
assign P = A ^ B;
assign C[0]=G[0]|(P[0]&C01);
assign C[1]=G[1]|(P[1]&C[0]);
assign C[2]=G[2]|(P[2]&C[1]);
assign C[3]=G[3]|(P[3]&C[2]);
always @(*) begin
  S[0] = P[0] ^ C01;
  S[1] = P[1] ^ C[0];
  S[2] = P[2] ^ C[1];
  S[3] = P[3] ^ C[2];
end
endmodule

2. Testbench代码

//filename:tb_ahead_Bene_C01rcuit.v
`timescale 10ns/1ns
module tb_ahead_gene_circuit;
reg [3:0] A,B;
reg C01;
wire  [3:0] C;
wire  [3:0] S;
ahead_gene_circuit U(A,B,C01,C,S);
initial    begin
	A=4'b0000;B=4'b0000;C01=0;
	#5;
	A=4'b1111;B=4'b1111;C01=0;
	#5;
	A=4'b1010;B=4'b1010;C01=1;
	#5;
	A=4'b1010;B=4'b1010;C01=1;
	#5;
    A=4'b0010;B=4'b1010;C01=1;
end
endmodule

3. 时序仿真图

在这里插入图片描述

五、CRC校验

1. 原理

循环冗余校验（Cyclic Redundancy Check， CRC）是一种根据网络数据包或计算机文件等数据产生简短固定位数校验码的一种信道编码技术，主要用来检测或校验数据传输或者保存后可能出现的错误。它是利用除法及余数的原理来作错误侦测的。(来源百度)

CRC即循环冗余校验码（Cyclic Redundancy Check）：是数据通信领域中最常用的一种查错校验码，其特征是信息字段和校验字段的长度可以任意选定。循环冗余检查（CRC）是一种数据传输检错功能，对数据进行多项式计算，并将得到的结果附在帧的后面，接收设备也执行类似的算法，以保证数据传输的正确性和完整性。（来自CRC在线计算小程序）

①CRC校验原理及实现
②CRC校验（一）——原理
③​史上解释CRC最清楚的文章
④FPGA手撕代码——CRC校验码的多种Verilog实现方式

从上面这四个博客就能学懂CRC了！
关于模2除法，其中进行加减的时候，就像是用异或来进行按位计算！

先粘贴一张图：
在这里插入图片描述
关于REFIN和REFOUT这两个参数的问题，是按照字节进行反转，在上面博客①这一点是没有说清楚的，并且其下的评论也有错误，在此详细说一下：
所谓的按照字节反转，就是每八位进行一下逆序，比如0x34，为8’b0011_0100,逆序为8’b0010_1100;一个例子容易引起误解，再举一个，比如0x415a，为16’b0100_0001_0101_1010,逆序之后为16’b1000_0010_0101_1010.

接下来关于代码的部分，就直接用第④个博客来写吧。直接上题目：

用Verilog实现CRC-8的串行计算，G(D)=D8+D2+D+1，计算流程如下图所示：

2. RTL代码

①并行计算，串行输出

//并行计算，串行输出
module crc_8(
    input       clk         ,
    input       rst         ,
    input       data_in     ,//串行输入数据
    input       data_valid  ,//指示标志，这个信号为1时，对应的data才是有效的
    input       crc_start   ,//CRC计算的开始信号，一个时钟信号的脉冲
    output reg  crc_out     ,//串行CRC的输出
    output reg  crc_valid    //CRC valid指示
);

reg [7:0] lfsr_q;       //寄存器输出端
reg [7:0] lfsr_c;       //寄存器输入端

//根据流程图，使用组合逻辑实现异或运算和数据的传递
always @(*) begin 
    lfsr_c[0] = lfsr_q[7] ^ data_in;
    lfsr_c[1] = lfsr_q[0] ^ lfsr_q[7] ^ data_in;
    lfsr_c[2] = lfsr_q[1] ^ lfsr_q[7] ^ data_in;
    lfsr_c[3] = lfsr_q[2];
    lfsr_c[4] = lfsr_q[3];
    lfsr_c[5] = lfsr_q[4];
    lfsr_c[6] = lfsr_q[5];
    lfsr_c[7] = lfsr_q[6];
end 

//寄存器的数据更新，即数据从输入端到输出端，要使用时序逻辑
always @ (posedge clk) begin 
    if(rst) begin 
        lfsr_q <= {
    8{
    1'b1}};    //寄存器初始化 此处全为1
    end 
    else begin 
        lfsr_q <= data_valid ? lfsr_c : lfsr_q; //输入数据有效则更新，无效则等待，保持原样
    end 
end 

//串行输出
reg [2:0] count;
always @ (posedge clk) begin 
    if(rst) begin 
        crc_out <= 0;
        count <= 0;
    end 
    else begin 
        if(data_valid) begin 
            crc_out <= data_in;
            crc_valid <= 1'b0;
        end 
        else if(crc_start)begin 
            count <= count + 1'b1;
            crc_out <= lfsr_q[7-count]; 
            crc_valid <= 1'b1;
        end 
        else begin
            crc_valid <= 1'b0;
        end 
    end 
end 
endmodule

②串行计算，串行输出

//串行计算，串行输出
module CRC_8(
    input       clk         ,
    input       rst         ,
    input       data_in     ,//串行输入数据
    input       data_valid  ,//指示标志，这个信号为1时，对应的data才是有效的
    input       crc_start   ,//CRC计算的开始信号，一个时钟信号的脉冲
    output reg  crc_out     ,//串行CRC的输出
    output reg  crc_valid    //CRC valid指示
    );

reg [7:0] crc_reg;
always @ (posedge clk) begin 
    if(rst) begin 
        crc_reg <= 8'hff; //初始化赋值全为1
    end 
    else begin 
        if(data_valid) begin  //当数据有效时，进行CRC计算
            crc_reg <= next_crc(data_in, crc_reg);
        end 
    end 
end 
//串行输出
reg [2:0] count;
always @ (posedge clk)
begin 
    if(rst) begin 
        crc_out <= 0;
        count <= 0;
    end 
    else begin 
        if(data_valid) begin 
            crc_out <= data_in;
            crc_valid <= 1'b0;
        end 
        else if(crc_start)begin 
            count <= count + 1'b1;
            crc_out <= crc_reg[7-count]; 
            crc_valid <= 1'b1;
        end 
        else begin
            crc_valid <= 1'b0;
        end 
    end 
end 
/*构建函数：根据输入信号data_in,跳转CRC的状态。设计逻辑为 ①将CRC寄存器的数据左移1位，低位补零 ： {current_crc[6:0],1'b0} ②新数额u的数据data_in和移出的CRC最高位做异或 ： current_crc[7]^data_in ③使用位拼接符对异或结果进行位扩展，CRC-8进行8位的扩展 ： {8{current_crc[7]^data_in} ④扩展后的数据和生成多项式进行与运算 ： {8{current_crc[7]^data_in}} & (8'h07) ⑤将①的数据和④的数据进行异或运算，得到CRC结果 上面这些，①是对CRC低位的处理，②~⑤是对CRC最高的的处理 这个8'h07，是因为题目要求的G（D）=D8+D2+D1+D0，而最高位的D8是不用管的，故应是 0000_0111 */
function [7:0] next_crc;
    input data_in;
    input [7:0] current_crc;
    
    begin 
        next_crc = {
    current_crc[6:0],1'b0} ^ ({
    8{
    current_crc[7]^data_in}} & (8'h07));
    end 

endfunction
endmodule

3. Testbench代码

module crc8_tb();
reg clk;
reg rst;
reg data_in;
reg data_valid;
reg crc_start;
wire crc_out;
wire crc_valid;
initial begin 
    clk = 0;
    rst = 1;
    #50;
    rst = 0;
    crc_start = 0;
    
    data_in = 1;
    data_valid = 1;
    #640;
    
    data_in = 0;
    data_valid = 0;
    crc_start = 1;
    #160;
    
    crc_start = 0;
    #100;
    $stop;
end
always #10 clk = ~clk;
CRC_8 U0(
    .clk(clk),
    .rst(rst),
    .data_in(data_in),
    .data_valid(data_valid),
    .crc_start(crc_start),
    .crc_out(crc_out),
    .crc_valid(crc_valid)
    );
endmodule

4. 时序仿真图

在这里插入图片描述

六、无毛刺的时钟切换电路

无毛刺的时钟切换电路（Glitch-free clock switching circuit）设计（Verilog）
上面这篇文章中说的“相关时钟”，指两个时钟频率成倍数，而“无关时钟”，指的是两个时钟无任何相关性，这种情况下的代码，可以用于任何情况下的时钟切换，但是这样相对于“相关时钟”这样有特定条件下的时钟切换，在电路以及代码上肯定会复杂一些。

指明一下，寄存器时钟端下面有一个圆圈表示下降沿触发，如果没有就是上升沿触发。

1. 相关时钟的无毛刺时钟切换

①电路

在这里插入图片描述

②RTL代码

module glitch_free (
    input       clk0,    // Clock
	input       clk1,
	input       select,
	input       rst_n,  // Asynchronous reset active low

	output      clkout
);
    wire mid_clk0_n, mid_clk1_n; //寄存器反相端输出
    wire mid_clk0, mid_clk1; //寄存器的输入端，即与门的输出
    reg mid_clk0_r, mid_clk1_r; //寄存器的输出端
    assign mid_clk1 = select & mid_clk0_n;
	assign mid_clk0 = ~select & mid_clk1_n;
    assign mid_clk0_n = ~mid_clk0_r;
    assign mid_clk1_n = ~mid_clk1_r;

    always @(negedge clk0 or negedge rst_n) begin
        if(!rst_n)
            mid_clk0_r <= 1'b0;
        else
            mid_clk0_r <= mid_clk0;
    end

    always @(negedge clk1 or negedge rst_n) begin
        if(!rst_n)
            mid_clk1_r <= 1'b0;
        else
            mid_clk1_r <= mid_clk1;
    end

    assign clkout = (mid_clk0_r & clk0) | (mid_clk1_r & clk1);
endmodule

③Testbench代码

`timescale 1ns / 1ps
module test_tb;
    reg clk0, clk1;
    reg select;
    wire clkout;
    
    initial begin
        clk0 = 0;
        forever
        #2 clk0 = ~clk0;
    end
    
    initial begin
        clk1 = 0;
        forever
        #5 clk1 = ~clk1;
    end
    
    
    reg rst_n;
    initial begin
        select = 0;
        rst_n = 0;
        #5
        rst_n = 1;
        #30
        select = 1;
        #40
        select = 0;
    end
   	glitch_free inst_glitch_free (.clk0(clk0), .clk1(clk1), .select(select), .rst_n(rst_n), .clkout(clkout));
endmodule

④时序仿真图

在这里插入图片描述

2. 无关时钟的无毛刺时钟切换

①电路

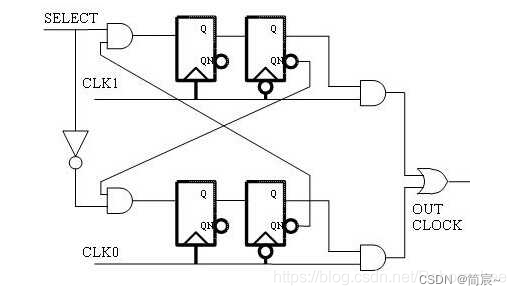
在这里插入图片描述

②RTL电路

module glitch_free (
	input clk0,    // Clock
	input clk1,
	input select,
	input rst_n,  // Asynchronous reset active low
	
	output clkout
);
 
	wire mid_clk0;
	reg mid_clk0_r1, mid_clk0_r2, mid_clk0_r2n;
	wire mid_clk1;
	reg mid_clk1_r1, mid_clk1_r2, mid_clk1_r2n;
 
	assign mid_clk1 = select & mid_clk0_r2n;
	assign mid_clk0 = ~select & mid_clk1_r2n;
	//第一级触发器用上升沿采样，选择信号与反馈信号的与运算
	[email protected](posedge clk1 or negedge rst_n) begin
		if(~rst_n) mid_clk1_r1 <= 0;
		else mid_clk1_r1 <= mid_clk1;
	end
	//第二级触发器用下降沿采样
	[email protected](negedge clk1 or negedge rst_n) begin
		if(~rst_n) begin
			mid_clk1_r2 <= 0;
			mid_clk1_r2n <= 1;
		end
		else begin
			mid_clk1_r2 <= mid_clk1_r1;
			mid_clk1_r2n <= ~mid_clk1_r1;
		end
	end
	//第一级触发器用上升沿采样，选择信号与反馈信号的与运算
	[email protected](posedge clk0 or negedge rst_n) begin
		if(~rst_n) mid_clk0_r1 <= 0;
		else mid_clk0_r1 <= mid_clk0;
	end
	//第二级触发器用下降沿采样
	[email protected](negedge clk0 or negedge rst_n) begin
		if(~rst_n) begin
			mid_clk0_r2 <= 0;
			mid_clk0_r2n <= 1;
		end
		else begin
			mid_clk0_r2 <= mid_clk0_r1;
			mid_clk0_r2n <= ~mid_clk0_r1;
		end
	end
	wire mid_clk11, mid_clk00;
	assign mid_clk11 = clk1 & mid_clk1_r2;
	assign mid_clk00 = clk0 & mid_clk0_r2;

	assign clkout = mid_clk11 | mid_clk00;
endmodule

仿真激励文件和上面是一样的。

七、无符号整数除法器-组合逻辑

Verilog – 无符号整数除法器（一）
数学运算（三）——无符号数除法器

小小总结一下：
无符号整数除法器，就是通过比较器与减法器，求出商和余数，有点类似于手算的那种除法过程，或者说是辗转相除法。
在这里插入图片描述
将摘抄下的流程图放下来，便于理解：
在这里插入图片描述

我就直接把代码给搬下来了！在这之前，先放一个例子的算法图吧：
在这里插入图片描述

1. RTL代码

module int_div(
input[31:0] a, 
input[31:0] b,
output reg [31:0] yshang,
output reg [31:0] yyushu
);
reg[31:0] tempa;
reg[31:0] tempb;
reg[63:0] temp_a;
reg[63:0] temp_b;
 
integer i;
always @(a or b) begin
    tempa <= a;
    tempb <= b;
end
 
always @(tempa or tempb) begin
    temp_a = {
    32'h00000000,tempa};
    temp_b = {
    tempb,32'h00000000}; 
    for(i = 0;i < 32;i = i + 1) begin
         temp_a = {
    temp_a[62:0],1'b0};
          if(temp_a[63:32] >= tempb)
              temp_a = temp_a - temp_b + 1'b1;
          else
		temp_a = temp_a;
      end
    yshang <= temp_a[31:0];
    yyushu <= temp_a[63:32];
end
endmodule

2. Testbench代码

`timescale 1ns/1ps
module div_fsm_tb();
parameter DATAWIDTH = 16;
reg  clk;
reg  rstn;       
reg  en;    
wire ready;     
reg  [DATAWIDTH-1:0]    dividend; 
reg  [DATAWIDTH-1:0]    divisor;
wire [DATAWIDTH-1:0]    quotient;
wire [DATAWIDTH-1:0]    remainder;
wire                    vld_out;

wire [DATAWIDTH-1:0]    quotient_ref; // true result
wire [DATAWIDTH-1:0]    remainder_ref; 
assign quotient_ref = dividend/divisor;
assign remainder_ref = dividend%divisor;

always #1 clk = ~clk;

integer i;
initial begin
  clk = 1;
  rstn = 1;
  en = 0;
  #2 rstn = 0; #2 rstn = 1;
  repeat(2) @(posedge clk);

  for(i=0;i<10;i=i+1) begin
    en <= 1;
    dividend <= $urandom()%1000;
    divisor  <= $urandom()%100;
    wait (ready == 1);
    wait (vld_out == 1);
  end
end
initial begin
    $fsdbDumpvars();
    $fsdbDumpMDA();
    $dumpvars();
    #1000 $finish;
 end

div_fsm #(
    .DATAWIDTH                      ( DATAWIDTH  ))
U_DIV_FSM_0(
    .clk                            ( clk        ),
    .rstn                           ( rstn       ),
    .en                             ( en         ),
    .ready                          ( ready      ),
    .dividend                       ( dividend   ),
    .divisor                        ( divisor    ),
    .quotient                       ( quotient   ),
    .remainder                      ( remainder  ),
    .vld_out                        ( vld_out    )
);
endmodule

3.时序仿真图

在这里插入图片描述
由于纯组合逻辑实现可能会有较大的延时，并且可能会综合出锁存器，因此采用时序逻辑的设计是更好的选择。

八、无符号整数除法器-时序逻辑

Verilog – 无符号整数除法器（二）
流程图和上面的是一样的，我直接按照我的习惯改一下代码，放在下面。

1. RTL代码

`timescale 1ns/1ps
module div_fsm  #(
parameter DATAWIDTH=8
)(
  input                       clk      ,
  input                       rstn     ,
  input                       en       , //使能标志
  output  wire                ready    , //标志信号位，在激励仿真中使用
  input  [DATAWIDTH-1:0]      dividend , //被除数
  input  [DATAWIDTH-1:0]      divisor  , //除数
  output wire [DATAWIDTH-1:0] quotient , //商
  output wire [DATAWIDTH-1:0] remainder, //余数
  output wire                 vld_out    //输出标志位，在仿真激励中使用
);

reg [DATAWIDTH*2-1:0] dividend_e ; //被除数，中间量
reg [DATAWIDTH*2-1:0] divisor_e  ; //除数，中间量
reg [DATAWIDTH-1:0]   quotient_e ; //商，中间量
reg [DATAWIDTH-1:0]   remainder_e; //余数，中间量
/*之所以要设置这样的中间量，是因为在有些仿真软件上，如果直接对定义的输出赋值，会报错，无法综合*/
reg [1:0] current_state,next_state;

reg [DATAWIDTH-1:0] count; //移位次数计数器

parameter IDLE =2'b00   ,
          SUB  =2'b01   ,
		  SHIFT=2'b10   ,
		  DONE =2'b11   ;

//状态机①：时序逻辑，传递寄存器状态
[email protected](posedge clk or negedge rstn)
  if(!rstn) current_state <= IDLE;
  else current_state <= next_state;
//状态机②：组合逻辑，根据当前状态和当前输入，确定下一状态机的状态 ,注意，这里要用非阻塞赋值
always @(*) begin
  next_state <= 2'bx;
  case(current_state)
    IDLE    : next_state <= en ? SUB :IDLE;
    SUB     : next_state <= SHIFT;
    SHIFT   : next_state <= (count<DATAWIDTH) ? SUB : DONE;
    DONE    : next_state <= IDLE;
  endcase
end
//状态机③：时序逻辑，根据当前状态和当前输入，确定输出信号
[email protected](posedge clk or negedge rstn) begin
 if(!rstn)begin
   dividend_e  <= 0;
   divisor_e   <= 0;
   quotient_e  <= 0;
   remainder_e <= 0;
   count       <= 0;
 end 
 else begin 
  case(current_state)
  IDLE:begin //对除数和被除数进行位拓展
         dividend_e <= {
    {
    DATAWIDTH{
    1'b0}},dividend};
	     divisor_e  <= {
    divisor,{
    DATAWIDTH{
    1'b0}}};
       end
  SUB:begin //被除数 >= 除数 ？ 被除数 = （被除数 - 除数 + 1） ： （移位） 
        if(dividend_e>=divisor_e)begin
           quotient_e <= {
    quotient_e[DATAWIDTH-2:0],1'b1};
		   dividend_e <= dividend_e-divisor_e;
         end
	    else begin
	       quotient_e <= {
    quotient_e[DATAWIDTH-2:0],1'b0};
		   dividend_e <= dividend_e;
        end
      end
  SHIFT:begin //移位次数 < 被除数位宽 ？ 被除数左移1位 ： 输出被除数当前值
	   if(count<DATAWIDTH)begin
	     dividend_e <= dividend_e<<1;
	     count      <= count+1;		 
       end
	   else begin
		 remainder_e <= dividend_e[DATAWIDTH*2-1:DATAWIDTH];
       end
     end
  DONE:begin
		count       <= 0;
  end	 
  endcase
 end
end
  
assign quotient  = quotient_e;
assign remainder = remainder_e;

assign ready=(current_state==IDLE)? 1'b1:1'b0;
assign vld_out=(current_state==DONE)? 1'b1:1'b0;
	       
endmodule

2. Testbench代码

`timescale 1ns/1ps
module div_fsm_tb();
parameter DATAWIDTH = 16;

reg  clk;
reg  rstn;       
reg  en;    
wire ready;     
reg  [DATAWIDTH-1:0]    dividend; 
reg  [DATAWIDTH-1:0]    divisor;
wire [DATAWIDTH-1:0]    quotient;
wire [DATAWIDTH-1:0]    remainder;
wire                    vld_out;

wire [DATAWIDTH-1:0]    quotient_ref; // true result
wire [DATAWIDTH-1:0]    remainder_ref; 
assign quotient_ref = dividend/divisor;
assign remainder_ref = dividend%divisor;

always #1 clk = ~clk;

integer i;
initial begin
  clk = 1;
  rstn = 1;
  en = 0;
  #2 rstn = 0; #2 rstn = 1;
  repeat(2) @(posedge clk);

  for(i=0;i<10;i=i+1) begin
    en <= 1;
    dividend <= $urandom()%1000;
    divisor  <= $urandom()%100;
    wait (ready == 1);
    wait (vld_out == 1);
  end
end

initial begin
    $fsdbDumpvars();
    $fsdbDumpMDA();
    $dumpvars();
    #1000 $finish;
 end

div_fsm #(
    .DATAWIDTH                      ( DATAWIDTH  ))
U_DIV_FSM_0(
    .clk                            ( clk        ),
    .rstn                           ( rstn       ),
    .en                             ( en         ),
    .ready                          ( ready      ),
    .dividend                       ( dividend   ),
    .divisor                        ( divisor    ),
    .quotient                       ( quotient   ),
    .remainder                      ( remainder  ),
    .vld_out                        ( vld_out    )
);
endmodule

3.时序仿真图

在这里插入图片描述

总结

代码为主！
很多东西确实很深奥的，要一点一点地去写会花费很多时间，所以也有直接把别人写的完整的博客放在这，也有把别人的东西直接拿过来的，不过都有注明（虽然不像写文献那样一一标注）。
我觉得这样对我的学习是有好处的，所以就这样做了。如果涉及到侵权，请与我联系；如果发现有什么错误，也请与我联系！谢谢！

原网站

版权声明
本文为[简宸~]所创，转载请带上原文链接，感谢
https://blog.csdn.net/weixin_41678913/article/details/124247122

边栏推荐

猜你喜欢

随机推荐