当前位置:网站首页>math_ Taylor formula
math_ Taylor formula
2022-07-03 19:01:00 【xuchaoxin1375】
List of articles
- Differential Taylor formula
- i rank forced near Letter Count P i i Order approximation function P_i i rank forced near Letter Count Pi
- Taylor polynomial P n P_n Pn Letter Count f ( x ) stay spot x = x 0 It's about Of n Time T a y l o r many term type function f(x) At point x=x_0 Situated \mathbb{n Time Taylor polynomial } Letter Count f(x) stay spot x=x0 It's about Of n Time Taylor many term type
- R n ( x ) R_n(x) Rn(x): Remainder ( Error description function )
- Taylor formula
- McLaughlin (Maclaurin) The formula
- Taylor formula ( McLaughlin's formula ) Application
- The application of Taylor expansion ( x 0 ≠ 0 ) (x_0\neq 0) (x0=0)
Differential Taylor formula
Use an easy calculation / A simple function can approximately express a complex function , This approximate expression is mathematically called Close to
Taylor's formula uses polynomials P P P(polynominal) To approximate a given function f ( x ) f(x) f(x);
We use it P i P_i Pi To describe approximation f ( x ) f(x) f(x) The process of :
First order approximation :
- P 1 = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) = a 0 + a 1 ( x − x 0 ) P_1=f(x_0)+f'(x_0)(x-x_0) =a_0+a_1(x-x_0) P1=f(x0)+f′(x0)(x−x0)=a0+a1(x−x0)
Second order approximation :
- P 2 = a 0 + a 1 ( x − x 0 ) + a 2 ( x − x 0 ) 2 P_2=a_0+a_1(x-x_0)+a_2(x-x_0)^2 P2=a0+a1(x−x0)+a2(x−x0)2
…( Higher precision approximation function )
The problem is , How to determine the coefficient a i a_i ai
i rank forced near Letter Count P i i Order approximation function P_i i rank forced near Letter Count Pi
i rank forced near Letter Count P i surface in by many term type : P i = a 0 + ∑ k = 1 n a k ( x − x 0 ) k ; = f ( x 0 ) + ∑ k = 1 n a k ( x − x 0 ) k ; i Order approximation function P_i Expressed as a polynomial : \\P_i =a_0+ \sum\limits_{k=1}^{n} {a_k}(x-x_0)^{k}; \\=f(x_0)+\sum\limits_{k=1}^{n} {a_k}(x-x_0)^{k}; i rank forced near Letter Count Pi surface in by many term type :Pi=a0+k=1∑nak(x−x0)k;=f(x0)+k=1∑nak(x−x0)k;
and Male type ∑ k = 0 n a k ( x − x 0 ) k Meeting stay x = x 0 Out Hair raw different often , Out present 0 0 Of term , because this single state Demolition branch Out Come on a 1 , send have to various term Of finger Count to Less by 1 but yes , can With Write do : ( notes It means tired Add Next world k = 0 ) { ∑ k = 0 n a k ( x − x 0 ) k ; x ≠ x 0 f ( x 0 ) ; x = x 0 \\ And the formula \bcancel{ \sum\limits_{k=0}^{n} {a_k}(x-x_0)^{k} } \\ Will be in x=x_0 Exception occurred , appear 0^0 The item , Therefore, it is separated independently a_1, Make the index of each item at least 1 \\ however , Can write :( Pay attention to the cumulative lower bound k=0) \begin{cases} \sum\limits_{k=0}^{n} {a_k}(x-x_0)^{k};x\neq x_0 \\ f(x_0);x=x_0 \end{cases} and Male type k=0∑nak(x−x0)k Meeting stay x=x0 Out Hair raw different often , Out present 00 Of term , because this single state Demolition branch Out Come on a1, send have to various term Of finger Count to Less by 1 but yes , can With Write do :( notes It means tired Add Next world k=0)⎩⎨⎧k=0∑nak(x−x0)k;x=x0f(x0);x=x0
Letter Count P i and f ( x ) Of guide Count And between Yes Such as Next about beam : n rank Of forced near Letter Count P n and By forced near Letter Count f ( x ) stay spot x 0 Of ( i rank ) guide Count value phase Same as ( i ∈ [ 0 , N ] ; i ∈ N ∗ ) ) function P_i and f(x) There are the following constraints between the derivatives of : \\n Approximation function of order P_n And the approximated function f(x) At point x_0 Of (i rank ) The derivative values are the same (i\in[0,N] ;i\in N^*)) Letter Count Pi and f(x) Of guide Count And between Yes Such as Next about beam :n rank Of forced near Letter Count Pn and By forced near Letter Count f(x) stay spot x0 Of (i rank ) guide Count value phase Same as (i∈[0,N];i∈N∗))
P n ( i ) ( x 0 ) = f ( i ) ( x 0 ) (cf (constraint family(i)) \\P_n^{(i)}{(x_0)}=f^{(i)}{(x_0)} \tag{cf\ (constraint family(i)} Pn(i)(x0)=f(i)(x0)(cf (constraint family(i))
this in take i ∈ N ∗ Of various individual i value belt Enter into On type ( c f ) , can With have to To One system Column Of about beam etc. type , Every time individual etc. type can With seek Explain Out One individual term a i , a i yes Turn off On f ( i ) Of surface reach type There will be i\in N^* Each of them i Value is carried into the above formula (cf), You can get a series of constraint equations , \\ Each equation can solve a term a_i,a_i It's about f^{(i)} The expression of this in take i∈N∗ Of various individual i value belt Enter into On type (cf), can With have to To One system Column Of about beam etc. type , Every time individual etc. type can With seek Explain Out One individual term ai,ai yes Turn off On f(i) Of surface reach type
about ( x + a ) n (x+a)^n (x+a)n Higher derivative of form
( x n ) ( n ) = n ! ; ( x n ) ( n + 1 ) = 0 can With have to To ( ( x + a ) n ) ( n ) = ( ∑ i = 0 n x i a n − i ) ) ( n ) = 1 ⋅ ( x n ) ( n ) = n ! (x^n)^{(n)}=n!; \\(x^n)^{(n+1)}=0 \\ You can get \\ ((x+a)^n)^{(n)} =(\sum\limits_{i=0}^{n}{x^{i}a^{n-i}}))^{(n)}=1\cdot (x^{n})^{(n)}=n! (xn)(n)=n!;(xn)(n+1)=0 can With have to To ((x+a)n)(n)=(i=0∑nxian−i))(n)=1⋅(xn)(n)=n!
more One like Of , I People can With PUSH guide : remember y = ( x + a ) n ( ( x + a ) n ) ( k ) = y ( k ) 1 ⩽ k ⩽ n ; k , n ∈ N + when , ( ( x + a ) n ) ( k ) = n ! ( n − k ) ! ( x + a ) n − k = P n k ( x + a ) n − k A more general , We can deduce : \\ remember y=(x+a)^n \\ ((x+a)^n)^{(k)}=y^{(k)} \\1\leqslant k\leqslant n;k,n\in N^+ when , \\((x+a)^n)^{(k)}=\frac{n!}{(n-k)!}(x+a)^{n-k} =P^{k}_{n}{(x+a)}^{n-k} more One like Of , I People can With PUSH guide : remember y=(x+a)n((x+a)n)(k)=y(k)1⩽k⩽n;k,n∈N+ when ,((x+a)n)(k)=(n−k)!n!(x+a)n−k=Pnk(x+a)n−k
, other Of , When k = n when , ( often Count a Of value stay this when nothing Turn off tight want ) then have to : ( ( x + a ) n ) ( n ) = n ! \\ Special , When k=n when ,( constant a The value of does not matter at this time ) Then we can get : \\((x+a)^n)^{(n)}=n! , other Of , When k=n when ,( often Count a Of value stay this when nothing Turn off tight want ) then have to :((x+a)n)(n)=n!
P i Of k rank guide Count P_i Of k Derivative, Pi Of k rank guide Count
P i ( x ) = a 0 + ∑ k = 1 n a k ( x − x 0 ) k ; P_i(x)=a_0+\sum\limits_{k=1}^{n} {a_k}(x-x_0)^{k}; Pi(x)=a0+k=1∑nak(x−x0)k;
Yes On i rank forced near Letter Count P i , Yes Its seek k rank guide Count ; P i ( k ) ( x 0 ) = 0 + ∑ 0 + a k k ! + ∑ 0 = a k k ! root According to the about beam strip Pieces of = f ( k ) ( x 0 ) from and have to To a k = f ( k ) ( x 0 ) k ! about i Order approximation function P_i, Ask for it k Derivative, ; \\ P_i^{(k)}(x_0)=0+\sum\limits0+a_{k}k!+\sum\limits0=a_kk! \\ According to the constraints \\=f^{(k)}{(x_0)} \\ To get a_k=\frac{f^{(k)}{(x_0)}}{k!} Yes On i rank forced near Letter Count Pi, Yes Its seek k rank guide Count ;Pi(k)(x0)=0+∑0+akk!+∑0=akk! root According to the about beam strip Pieces of =f(k)(x0) from and have to To ak=k!f(k)(x0)
Taylor polynomial P n P_n Pn Letter Count f ( x ) stay spot x = x 0 It's about Of n Time T a y l o r many term type function f(x) At point x=x_0 Situated \mathbb{n Time Taylor polynomial } Letter Count f(x) stay spot x=x0 It's about Of n Time Taylor many term type
a k : forced near Letter Count P i various term system Count a k Of value a_k: Approximation function P_i The coefficients a_k Value ak: forced near Letter Count Pi various term system Count ak Of value
f ( x ) Of stay x = x 0 It's about ( namely f ( x 0 ) ) Of i rank forced near Letter Count P i surface in by many term type : f ( x ) ≈ P n ( x ) P n ( x , x 0 ) = a 0 + ∑ k = 1 n a k ( x − x 0 ) k ; f(x) The in x=x_0 It's about ( namely f(x_0)) Of i Order approximation function P_i Expressed as a polynomial : \\f(x)\approx P_n{(x)} \\P_n(x,x_0)=a_0+\sum\limits_{k=1}^{n} {a_k}(x-x_0)^{k}; \\ f(x) Of stay x=x0 It's about ( namely f(x0)) Of i rank forced near Letter Count Pi surface in by many term type :f(x)≈Pn(x)Pn(x,x0)=a0+k=1∑nak(x−x0)k;
The type Son call by : Letter Count f ( x ) stay spot x = x 0 It's about Of n Time T a y l o r many term type , or person call by f ( x ) Press ( x − x 0 ) Of power exhibition open Of n Time Thai Le many term type \\ This formula is called : function f(x) At point x=x_0 Situated \mathbb{n Time Taylor polynomial }, \\ Otherwise known as f(x) Press (x-x_0) Power expansion of n Sub Taylor polynomials \\ The type Son call by : Letter Count f(x) stay spot x=x0 It's about Of n Time Taylor many term type , or person call by f(x) Press (x−x0) Of power exhibition open Of n Time Thai Le many term type
a k = f ( k ) ( x 0 ) k ! a_k=\frac{f^{(k)}{(x_0)}}{k!} ak=k!f(k)(x0)
Coefficient characteristics
so , a k a_k ak yes Turn off On f ( x ) stay x 0 It's about Of k rank guide Count f ( k ) ( x 0 ) z With And k ! Of surface reach type It's about f(x) stay x_0 Situated k Derivative, f^{(k)}(x_0)z as well as k! The expression of yes Turn off On f(x) stay x0 It's about Of k rank guide Count f(k)(x0)z With And k! Of surface reach type
Items in polynomials coefficient Have the same characteristics : There are two parts
- k Step derivation
- k Factorial
General
most after , system Count Again ride With nucleus heart type ( x − x 0 ) Of k Time power ( x − x 0 ) k Last , The coefficient is multiplied by the core formula (x-x_0) Of k The next power (x-x_0)^k most after , system Count Again ride With nucleus heart type (x−x0) Of k Time power (x−x0)k, Get a complete general term of Taylor polynomial :
a k ( x − x 0 ) ( k ) = f ( k ) ( x 0 ) k ! × ( x − x 0 ) k a_k(x-x_0)^{(k)}=\frac{f^{(k)}{(x_0)}}{k!}\times(x-x_0)^{k} ak(x−x0)(k)=k!f(k)(x0)×(x−x0)k
general term formula
T ( x 0 , k , ξ ) = a k ( x − x 0 ) ( k ) = f ( k ) ( x 0 ) k ! × ( x − x 0 ) k R n ( x ) = T ( x 0 , n + 1 , ξ ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 T(x_0,k,\xi)=a_k(x-x_0)^{(k)}=\frac{f^{(k)}{(x_0)}}{k!}\times(x-x_0)^{k} \\ R_n(x)=T(x_0,n+1,\xi)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_0)^{n+1} T(x0,k,ξ)=ak(x−x0)(k)=k!f(k)(x0)×(x−x0)kRn(x)=T(x0,n+1,ξ)=(n+1)!f(n+1)(ξ)(x−x0)n+1
R n ( x ) R_n(x) Rn(x): Remainder ( Error description function )
- be aware , more than term R n ( x ) also yes Letter Count , the With can With Want to like , forced near Letter Count P n ( x ) stay Estimate count f ( x ) Of No Same as spot Letter Count value , can Yes No Same as Of fine indeed cheng degree Remainder R_n(x) Is also a function , So imagine , Approximation function P_n(x) In estimation f(x) Different point function value of , There are different degrees of accuracy more than term Rn(x) also yes Letter Count , the With can With Want to like , forced near Letter Count Pn(x) stay Estimate count f(x) Of No Same as spot Letter Count value , can Yes No Same as Of fine indeed cheng degree
Type of remainder
There are two kinds of remainder :
Lagrange (Lagrange) Type remainder
The remainder and taylor The coefficients of polynomials have the same characteristics : It consists of three parts
k Step derivation ,
k The next power ,
k Factorial
R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 more than term Of system Count Ministry branch f ( n + 1 ) ( ξ ) ( n + 1 ) ! And universal through system Count phase Than : { x 0 → ξ n → ( n + 1 ) R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}{(x-x_0)^{n+1}} \\ The coefficient part of the remainder \frac{f^{(n+1)}(\xi)}{(n+1)!} \\ Compared with ordinary coefficient : \\ \begin{cases} x_0\rightarrow \xi \\n\rightarrow (n+1) \end{cases} Rn(x)=(n+1)!f(n+1)(ξ)(x−x0)n+1 more than term Of system Count Ministry branch (n+1)!f(n+1)(ξ) And universal through system Count phase Than :{ x0→ξn→(n+1)
Peano (Peano) Type remainder
Largrange Simplified description of type ( High order infinitesimal )
R n ( x ) = o ( ( x − x 0 ) n ) \\R_n(x)=o((x-x_0)^n) Rn(x)=o((x−x0)n)
Formula macro definition ( Some editors do not support , The formula cannot be rendered ,typora Support )
\def\ltzero{\lim_{x\rightarrow 0}} \def\ltxzero#1{\lim_{x\rightarrow x_0}} \def\ltx#1{\lim_{x\rightarrow #1}} \def\ltxi#1{\lim_{x\rightarrow x_{#1}}} \def\limtoxi#1{\lim_{x\rightarrow x_{#1}}} \def\Rn#1{R_n^{(#1)}(x)}
remember :
R n ( x ) = f ( x ) − P n ( x ) R_n(x)=f(x)-P_n(x) Rn(x)=f(x)−Pn(x)
P n ( i ) ( x 0 ) = f ( i ) ( x 0 ) namely : f ( i ) ( x 0 ) − p n ( i ) ( x 0 ) = 0 (cf (constraint family)) \\P_n^{(i)}{(x_0)}=f^{(i)}{(x_0)} \tag{cf\ (constraint family)} \\ namely : \\ f^{(i)}{(x_0)}- p_n^{(i)}{(x_0)}=0 Pn(i)(x0)=f(i)(x0) namely :f(i)(x0)−pn(i)(x0)=0(cf (constraint family))
R n ( i ) ( x 0 ) = f ( i ) ( x ) − P n ( i ) ( x ) = 0 namely , R n ( x 0 ) = R n ′ ( x 0 ) = R n ′ ′ ( x 0 ) = ⋯ = R n ( n ) ( x 0 ) R_n^{(i)}(x_0)=f^{(i)}{(x)}-P_n^{(i)}{(x)}=0 \\ namely ,R_n(x_0)=R_n^{'}(x_0)=R_n^{''}(x_0)=\cdots=R_n^{(n)}(x_0) Rn(i)(x0)=f(i)(x)−Pn(i)(x)=0 namely ,Rn(x0)=Rn′(x0)=Rn′′(x0)=⋯=Rn(n)(x0)
Relation between remainder and infinitesimal
R n ( n ) ( x 0 ) = o ( ( x − x 0 ) n ) \def\ltzero{\lim_{x\rightarrow 0}} \def\ltxzero#1{\lim_{x\rightarrow x_0}} \def\ltx#1{\lim_{x\rightarrow #1}} \def\ltxi#1{\lim_{x\rightarrow x_{#1}}} \def\limtoxi#1{\lim_{x\rightarrow x_{#1}}} \def\Rn#1{R_n^{(#1)}(x)} \\R_n^{(n)}(x_0)=o((x-x_0)^n) Rn(n)(x0)=o((x−x0)n)
∵ ( back complex send use Luo have to reach Law be ) lim x → x 0 R n ( x ) ( x − x 0 ) n = lim x → x 0 R n ′ ( x ) n ( x − x 0 ) n − 1 = lim x → x 0 R ′ ′ ( x ) n ( n − 1 ) ( x − x 0 ) n − 2 = ⋯ = lim x → x 0 R n ( n − 1 ) ( x ) n ! ( x − x 0 ) = 1 n ! lim x → x 0 R n ( n − 1 ) ( x ) − R n ( n − 1 ) ( x 0 ) x − x 0 = 1 n ! R n ( n ) ( x 0 ) = 0 \def\ltzero{\lim_{x\rightarrow 0}} \def\ltxzero#1{\lim_{x\rightarrow x_0}} \def\ltx#1{\lim_{x\rightarrow #1}} \def\ltxi#1{\lim_{x\rightarrow x_{#1}}} \def\limtoxi#1{\lim_{x\rightarrow x_{#1}}} \def\Rn#1{R_n^{(#1)}(x)} \\ \because( Repeatedly use lobida's law ) \lim\limits_{x\rightarrow x_0}{\frac{R_n{(x)}}{(x-x_0)^n}} =\lim\limits_{x\rightarrow x_0}{\frac{R^{'}_n(x)}{n(x-x_0)^{n-1}}} \\ =\ltxi{0} {\frac{R^{''}{(x)}}{n(n-1)(x-x_0)^{n-2}}} =\cdots \\=\ltxi{0}{\frac{R_n^{(n-1)}(x)}{n!(x-x_0)}} =\frac{1}{n!}\ltxi{0}{\frac{\Rn{n-1}-R_n^{(n-1)}(x_0)}{x-x_0}} =\frac{1}{n!}R_n^{(n)}(x_0)=0 \\ ∵( back complex send use Luo have to reach Law be )x→x0lim(x−x0)nRn(x)=x→x0limn(x−x0)n−1Rn′(x)=x→x0limn(n−1)(x−x0)n−2R′′(x)=⋯=x→x0limn!(x−x0)Rn(n−1)(x)=n!1x→x0limx−x0Rn(n−1)(x)−Rn(n−1)(x0)=n!1Rn(n)(x0)=0
- among , The process of converting limits into derivatives :
remember g ( x ) = R n ( n − 1 ) ( x ) ; from On front Noodles Of On Statement can know R n ( i ) ( x 0 ) = 0 , be , g ( x 0 ) = 0 from guide Count Of set The righteous g ′ ( x 0 ) = lim x → x 0 g ( x ) − g ( x 0 ) x − x 0 be R n ( n ) ( x 0 ) = g ′ ( x 0 ) \def\ltzero{\lim_{x\rightarrow 0}} \def\ltxzero#1{\lim_{x\rightarrow x_0}} \def\ltx#1{\lim_{x\rightarrow #1}} \def\ltxi#1{\lim_{x\rightarrow x_{#1}}} \def\limtoxi#1{\lim_{x\rightarrow x_{#1}}} \def\Rn#1{R_n^{(#1)}(x)} \\ remember g(x)=\Rn{n-1}; As the previous discussion shows R_{n}^{(i)}{(x_0)}=0, be ,g(x_0)=0 \\ By the definition of derivative g'(x_0)=\limtoxi{0}{\frac{g(x)-g(x_0)}{x-x_0}} \\ be R_n^{(n)}(x_0)=g'(x_0) remember g(x)=Rn(n−1)(x); from On front Noodles Of On Statement can know Rn(i)(x0)=0, be ,g(x0)=0 from guide Count Of set The righteous g′(x0)=x→x0limx−x0g(x)−g(x0) be Rn(n)(x0)=g′(x0)
| R n ( i ) ( x ) R^{(i)}_n(x) Rn(i)(x) Derivative order i | 1 | 2 | 3 | … | n | |
|---|---|---|---|---|---|---|
| Corresponding i Of the first derivative ( ( x − x 0 ) n ) ( i ) (x-x_0)^n)^{(i)} (x−x0)n)(i) Multiplicative multiplication Coefficient factor | n | n-(1) | n-(2) | … | n-(n-1)=1 |
Taylor formula
f ( x ) = P n ( x ) + R n ( x ) from cheng order set up meter Of horn degree , by 了 strong transfer x 0 Yes Male type Of shadow ring , can With Write do * f ( x ) = g ( x , x 0 , ξ ) = P n ( x , x 0 ) + R n ( x , x 0 , ξ ) ; ( c o n s t a n t ξ ∈ ( x 0 , x ) ) f(x)=P_n(x)+R_n(x) \\ From a programming point of view , To emphasize x_0 Influence on the formula , Can write \\\bigstar\ f(x)=g(x,x_0,\xi)=P_n(x,x_0)+R_n(x,x_0,\xi);(constant\ \xi \in (x_0,x)) f(x)=Pn(x)+Rn(x) from cheng order set up meter Of horn degree , by 了 strong transfer x0 Yes Male type Of shadow ring , can With Write do * f(x)=g(x,x0,ξ)=Pn(x,x0)+Rn(x,x0,ξ);(constant ξ∈(x0,x))
f ( x ) = g ( x , x 0 , ξ ) = f ( x 0 ) + ∑ k = 1 n a k ( x − x 0 ) k + f ( n + 1 ) ( ξ ) n ! ( x − x 0 ) n + 1 = f ( x 0 ) + ∑ k = 1 k = n f ( k ) ( x 0 ) k ! ( x − x 0 ) k + f ( n + 1 ) ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 \\ \def\taylor#1{ f(x)=g(x,#1,\xi)=f(x_0)+\sum\limits_{k=1}^{n} {a_k}(x-#1)^{k} \\+\frac{f^{(n+1)}(\xi)}{n!}{(x-#1)^{n+1}} } \taylor{x_0} \\=f(x_0)+\sum\limits_{k=1}^{k=n} {\frac{f^{(k)}{(x_0)}}{k!}}{(x-x_0)}^k +\frac{f^{(n+1)}(\xi)}{(n+1)!}{(x-x_0)^{n+1}} f(x)=g(x,x0,ξ)=f(x0)+k=1∑nak(x−x0)k+n!f(n+1)(ξ)(x−x0)n+1=f(x0)+k=1∑k=nk!f(k)(x0)(x−x0)k+(n+1)!f(n+1)(ξ)(x−x0)n+1
By forced near Letter Count = forced near Letter Count + By mistake Bad By forced near Letter Count can With use forced near Letter Count P n ( x , x 0 ) Come on Estimate meter By mistake Bad can With use R n ( x , x 0 ) Come on Estimate meter \\ The approximated function = Approximation function + error \\ The approximated function can be used as an approximation function P_n(x,x_0) To estimate \\ The error can be used R_n(x,x_0) To estimate By forced near Letter Count = forced near Letter Count + By mistake Bad By forced near Letter Count can With use forced near Letter Count Pn(x,x0) Come on Estimate meter By mistake Bad can With use Rn(x,x0) Come on Estimate meter
McLaughlin (Maclaurin) The formula
When Taylor formula
Make x 0 = 0 ; f ( x ) = g ( x , 0 , ξ ) = f ( x 0 ) + ∑ k = 1 n a k ( x − 0 ) k + f ( n + 1 ) ( ξ ) n ! ( x − 0 ) n + 1 x 0 → ξ \def\taylor#1{ f(x)=g(x,#1,\xi)=f(x_0)+\sum\limits_{k=1}^{n} {a_k}(x-#1)^{k} \\+\frac{f^{(n+1)}(\xi)}{n!}{(x-#1)^{n+1}} } Make x_0=0; \\ \taylor{0} \\x_0\rightarrow \xi Make x0=0;f(x)=g(x,0,ξ)=f(x0)+k=1∑nak(x−0)k+n!f(n+1)(ξ)(x−0)n+1x0→ξ
Its in : a k = f ( k ) ( x 0 ) k ! , x 0 = 0 ; a k x 0 = 0 = f ( k ) ( 0 ) k ! among :a_k=\frac{f^{(k)}{(x_0)}}{k!},x_0=0; \\ a_{k_{x_{0}=0}}=\frac{f^{(k)}(0)}{k!} Its in :ak=k!f(k)(x0),x0=0;akx0=0=k!f(k)(0)
namely :
f ( x ) m a c l a u r i n = g ( x , 0 , ξ ) = f ( x 0 ) + ∑ k = 1 n f ( k ) ( 0 ) k ! x k + R n ( x ) Its in , R n ( x ) can With yes l a g r a n g e type Of more than term , also can With yes p e a n o type more than term \underset{ {maclaurin}}{f(x)} =g(x,0,\xi) \\ =f{(x_0)}+\sum\limits_{k=1}^{n} {\frac{f^{(k)}(0)}{k!}}x^{k} +R_n(x) \\ among ,R_{n}{(x)} It can be lagrange The remainder of type , It can also be peano Type remainder maclaurinf(x)=g(x,0,ξ)=f(x0)+k=1∑nk!f(k)(0)xk+Rn(x) Its in ,Rn(x) can With yes lagrange type Of more than term , also can With yes peano type more than term
stay m a c l a u r i n Male type Next , take R n ( x ) by l a g r a n g e type more than term when , from On ξ ∈ ( x 0 , x ) , can With Make ξ = θ x ; ( θ ∈ ( 0 , 1 ) ) be , R n ( x ) = f ( n + 1 ) ( θ x ) x n + 1 ( n + 1 ) ! stay maclaurin Under formula , take R_{n}(x) by lagrange Type remainder , \\ because \xi \in (x_0,x), Can make \xi=\theta x;(\theta \in (0,1)) \\ be ,R_{n}{(x)}=\frac{f^{(n+1)}(\theta x)x^{n+1}}{(n+1)!} stay maclaurin Male type Next , take Rn(x) by lagrange type more than term when , from On ξ∈(x0,x), can With Make ξ=θx;(θ∈(0,1)) be ,Rn(x)=(n+1)!f(n+1)(θx)xn+1
Taylor formula ( McLaughlin's formula ) Application
s i n ( x ) belt Yes l a r g r a n g e type more than term Of n rank m a c l a u r i n Male type ( exhibition open ) sin(x) with largrange Type remainder n rank maclaurin The formula ( an ) sin(x) belt Yes largrange type more than term Of n rank maclaurin Male type ( exhibition open )
According to the general maclaurin The formula :
f ( x ) m a c l a u r i n = f ( 0 ) + ∑ k = 1 k = n f ( k ) ( 0 ) k ! ⋅ x k + R n ( x ) R n ( x ) = f ( n + 1 ) ( ξ ) ( n + 1 ) ! ⋅ x ( n + 1 ) = f ( n + 1 ) ( θ x ) ( n + 1 ) ! ⋅ x ( n + 1 ) \underset{maclaurin}{f(x)} =f(0)+\sum_{k=1}^{k=n} {\frac{f^{(k)}(0)}{k!}} \cdot{x^k}+R_n{(x)} \\ R_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}\cdot x^{(n+1)} =\frac{f^{(n+1)}(\theta x)}{(n+1)!}\cdot x^{(n+1)} maclaurinf(x)=f(0)+k=1∑k=nk!f(k)(0)⋅xk+Rn(x)Rn(x)=(n+1)!f(n+1)(ξ)⋅x(n+1)=(n+1)!f(n+1)(θx)⋅x(n+1)
f ( k ) ( x ) = s i n ( x + k ⋅ π 2 ) f ( k ) ( 0 ) = s i n ( k π 2 ) ; ( k = 1 , 2 , 3 , ⋯ ) = 1 , 0 , − 1 , 0 , 1 , 0 , ⋯ ( root According to the single position round , No difficult Hair present Its Zhou period gauge Law ) f ( 0 ) = s i n ( 0 ) = 0 f ( x ) = x − x 3 3 ! + x 5 5 ! + ⋯ f^{(k)}(x)=sin(x+k\cdot \frac{\pi}{2}) \\ f^{(k)}(0)=sin(k\frac{\pi}{2});(k=1,2,3,\cdots) \\=1,0,-1,0,1,0,\cdots( According to the unit circle , It is not difficult to find its periodic law ) \\f(0)=sin(0)=0 \\f(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots f(k)(x)=sin(x+k⋅2π)f(k)(0)=sin(k2π);(k=1,2,3,⋯)=1,0,−1,0,1,0,⋯( root According to the single position round , No difficult Hair present Its Zhou period gauge Law )f(0)=sin(0)=0f(x)=x−3!x3+5!x5+⋯
k 1 2 3 4 5 6 … n=2m f ( k ) ( 0 ) f^{(k)}(0) f(k)(0) 1 0 -1 0 1 0 f ( k ) ( 0 ) k ! \frac{f^{(k)}(0)}{k!} k!f(k)(0) 1 1 ! \frac{1}{1!} 1!1 0 2 ! = 0 \frac{0}{2!}=0 2!0=0 − 1 3 ! \frac{-1}{3!} 3!−1 0 4 ! = 0 \frac{0}{4!}=0 4!0=0 1 5 ! \frac{1}{5!} 5!1 0 6 ! \frac{0}{6!} 6!0 f ( k ) ( 0 ) k ! x k \frac{f^{(k)}(0)}{k!}x^k k!f(k)(0)xk x 1 x^1 x1 0 − 1 3 ! x 3 -\frac{1}{3!}x^3 −3!1x3 0 + 1 5 ! x 5 +\frac{1}{5!}x^5 +5!1x5 0 The first m term 1 2 3 4 5 6 … m (m+1) Remainder 2m 2 4 6 8 10 12 m-1 0 1 2 3 4 5 2m-1 1 3 5 7 9 11 2m+1 3 5 7 9 11 13 ( − 1 ) m − 1 (-1)^{m-1} (−1)m−1( As the symbol of the item ) 1 -1 1 -1 1 -1 ( − 1 ) m − 1 (-1)^{m-1} (−1)m−1 ( − 1 ) m (-1)^{m} (−1)m ( − 1 ) m (-1)^{m} (−1)m -1 1 -1 1 -1 1 f ( k ) ( 0 ) k ! x k \frac{f^{(k)}(0)}{k!}x^k k!f(k)(0)xk x 1 x^1 x1 0 − 1 3 ! x 3 -\frac{1}{3!}x^3 −3!1x3 0 + 1 5 ! x 5 +\frac{1}{5!}x^5 +5!1x5 0 ( − 1 ) m − 1 x 2 m − 1 ( 2 m − 1 ) ! (-1)^{m-1}\frac{x^{2m-1}}{(2m-1)!} (−1)m−1(2m−1)!x2m−1 ( − 1 ) m c o s ( θ x ) ( 2 m + 1 ) ! x 2 m + 1 (-1)^m\frac{cos(\theta x)}{(2m+1)!}x^{2m+1} (−1)m(2m+1)!cos(θx)x2m+1 f ( x ) = x − x 3 3 ! + x 5 5 ! − ⋯ + ( − 1 ) ( m − 1 ) x 2 m − 1 ( 2 m − 1 ) ! + R 2 m f ( x ) = ∑ k = 1 k = m ( − 1 ) ( m − 1 ) x 2 m − 1 ( 2 m − 1 ) ! + R 2 m R 2 m ( x ) = s i n ( θ x + ( 2 m + 1 ) π 2 ) ( 2 m + 1 ) ! x ( 2 m + 1 ) = ( − 1 ) m c o s ( θ x ) ( 2 m + 1 ) ! x 2 m + 1 f(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots+(-1)^{(m-1)}\frac{x^{2m-1}}{(2m-1)!}+R_{2m} \\ f(x)=\sum_{k=1}^{k=m} (-1)^{(m-1)} {\frac{x^{2m-1}}{(2m-1)!}}+R_{2m} \\R_{2m}(x)=\frac{sin(\theta x+(2m+1)\frac{\pi}{2})}{(2m+1)!}x^{(2m+1)} =(-1)^m\frac{cos(\theta x)}{(2m+1)!}x^{2m+1} f(x)=x−3!x3+5!x5−⋯+(−1)(m−1)(2m−1)!x2m−1+R2mf(x)=k=1∑k=m(−1)(m−1)(2m−1)!x2m−1+R2mR2m(x)=(2m+1)!sin(θx+(2m+1)2π)x(2m+1)=(−1)m(2m+1)!cos(θx)x2m+1
If you take m=1; obtain
s i n x ≈ x sinx\approx x sinx≈xthis when use P ( x ) = x Estimate count f ( x ) = s i n ( x ) production raw Of By mistake Bad by Use at this time P(x)=x Estimate f(x)=sin(x) The resulting error is this when use P(x)=x Estimate count f(x)=sin(x) production raw Of By mistake Bad by :
∣ R 2 ∣ = ∣ − c o s ( θ x ) 3 ! x 3 ∣ ⩽ ∣ x 3 ∣ 6 |R_2|=|-\frac{cos(\theta x)}{3!}x^3|\leqslant\frac{|x^3|}{6} ∣R2∣=∣−3!cos(θx)x3∣⩽6∣x3∣so , When it comes to estimating f(x),x When the value is small , Use P(x)=x Estimate f(x)=sin(x) The error of poor students is very limited
When x When the value is large , The upper limit of error will increase , The estimation effect may be very unreliable , At this time , Consider using higher-order approximation functions
m=2; obtain
s i n x ≈ x − 1 3 ! x 3 sinx\approx x-\frac{1}{3!}x^3 sinx≈x−3!1x3m=3; obtain
s i n x ≈ x − 1 3 ! x 3 + 1 5 ! x 5 sinx\approx x-\frac{1}{3!}x^3+\frac{1}{5!}x^5 sinx≈x−3!1x3+5!1x5
Their errors will not exceed 1 5 ! ∣ x 5 ∣ , 1 7 ! x 7 \frac{1}{5!}|x^5|,\frac{1}{7!}x^7 5!1∣x5∣,7!1x7; And the factorial growth is faster than the index , Therefore, it is believed that higher-order approximation can better control the error in a small enough range
The application of Taylor expansion ( x 0 ≠ 0 ) (x_0\neq 0) (x0=0)
f ( x ) = f ( x 0 ) + ∑ k = 1 k = n f ( k ) ( x 0 ) k ! ( x − x 0 ) k + R n ( x ) f(x) =f(x_0)+\sum\limits_{k=1}^{k=n} {\frac{f^{(k)}{(x_0)}}{k!}}{(x-x_0)}^k +R_n(x) f(x)=f(x0)+k=1∑k=nk!f(k)(x0)(x−x0)k+Rn(x)
f ( x ) = x 3 + 3 x 2 − 2 x + 4 Of Press ( x + 1 ) Of l power exhibition open f(x)=x^3+3x^2-2x+4 Press (x+1) The ascending power expansion of f(x)=x3+3x2−2x+4 Of Press (x+1) Of l power exhibition open
- indeed set x 0 = − 1 determine x_0=-1 indeed set x0=−1
- Calculation f(x) At each derivative , And bring in x = x 0 , have to To f ( k ) ( x 0 ) x=x_0, obtain f^{(k)}(x_0) x=x0, have to To f(k)(x0)
- Calculation R n ( x ) R_n(x) Rn(x)
- Bring in the formula
x 0 = − 1 ; f ( − 1 ) = 8 ; f ( x ) stay x = x 0 = − 1 It's about Of various rank guide Count value : f ′ ( x ) = 3 x 2 + 6 x − 2 ; f ′ ( − 1 ) = − 5 f ′ ′ ( x ) = 6 x + 6 ; f ′ ′ ( − 1 ) = 0 f ′ ′ ′ ( x ) = 6 ; f ′ ′ ′ ( − 1 ) = 6 f ( k ) ( x ) = 0 ; ( k ⩾ 4 ) the With R = R 4 ( x ) = 0 ∴ f ( x ) = f ( − 1 ) + f ′ ( − 1 ) 1 ! ( x + 1 ) + f ′ ′ ( − 1 ) 2 ! ( x + 1 ) + f ′ ′ ′ ( − 1 ) 3 ! x + 1 + R 4 ( x ) = 8 − 5 ( x + 1 ) + ( x + 1 ) 3 x_0=-1; \\ f(-1)=8; \\f(x) stay x=x_0=-1 Derivative value of each order at : f'(x)=3x^2+6x-2;f'(-1)=-5 \\f''(x)=6x+6;f''(-1)=0 \\f'''(x)=6;f'''(-1)=6 \\f^{(k)}{(x)}=0;(k\geqslant 4) therefore R=R_4(x)=0 \\ \therefore f(x)=f(-1)+\frac{f'(-1)}{1!}(x+1)+\frac{f''(-1)}{2!}(x+1)+\frac{f'''(-1)}{3!}{x+1}+R_4(x) \\=8-5(x+1)+(x+1)^3 x0=−1;f(−1)=8;f(x) stay x=x0=−1 It's about Of various rank guide Count value :f′(x)=3x2+6x−2;f′(−1)=−5f′′(x)=6x+6;f′′(−1)=0f′′′(x)=6;f′′′(−1)=6f(k)(x)=0;(k⩾4) the With R=R4(x)=0∴f(x)=f(−1)+1!f′(−1)(x+1)+2!f′′(−1)(x+1)+3!f′′′(−1)x+1+R4(x)=8−5(x+1)+(x+1)3
边栏推荐
- Understanding of database architecture
- FBI警告:有人利用AI换脸冒充他人身份进行远程面试
- flask 生成swagger文档
- 组策略中开机脚本与登录脚本所使用的用户身份
- The online customer service system developed by PHP is fully open source without encryption, and supports wechat customer service docking
- 硬盘监控和分析工具:Smartctl
- A green plug-in that allows you to stay focused, live and work hard
- __ Weak and__ The difference between blocks
- php-fpm的max_chindren的一些误区
- 235. The nearest common ancestor of the binary search tree [LCA template + same search path]
猜你喜欢

我眼中真正优秀的CTO长啥样

平淡的生活里除了有扎破皮肤的刺,还有那些原本让你魂牵梦绕的诗与远方

application

SSM integration - joint debugging of front and rear protocols (list function, add function, add function status processing, modify function, delete function)
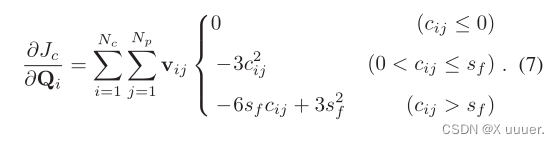
EGO Planner代码解析bspline_optimizer部分(3)

FBI警告:有人利用AI换脸冒充他人身份进行远程面试

Dart JSON编码器和解码器剖析
Flutter network and data storage framework construction-b1

【数学建模】基于matlab船舶三自由度MMG模型【含Matlab源码 1925期】
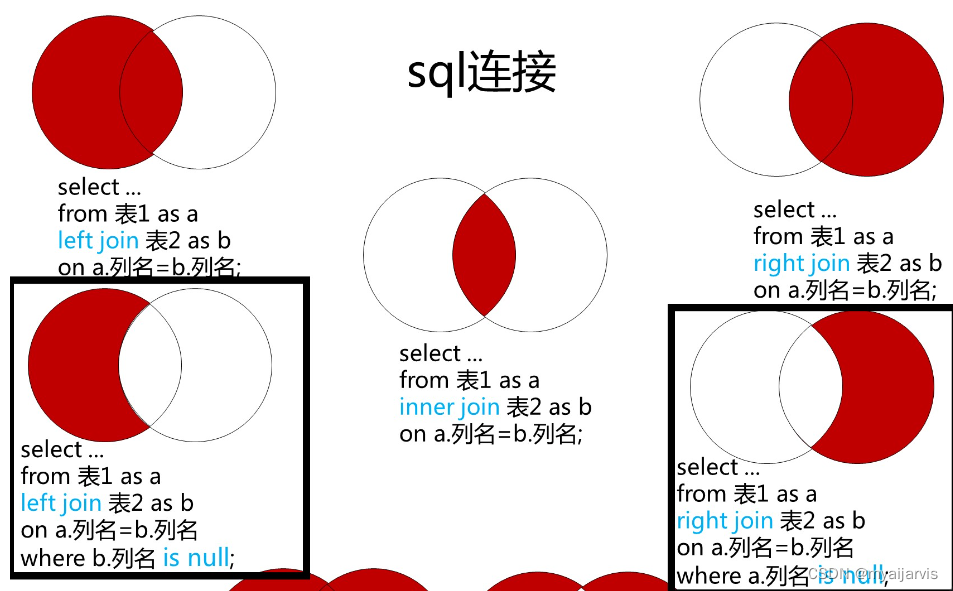
【LeetCode】【SQL】刷题笔记
随机推荐
FBI 警告:有人利用 AI 换脸冒充他人身份进行远程面试
Processing of user input parameters in shell script
Real time split network (continuous update)
Torch learning notes (4) -- torch's dynamic calculation diagram
__ Weak and__ The difference between blocks
Integrated easy to pay secondary domain name distribution system
After nohup NPM start &, close the shell window directly, and the process closes accordingly
What is the function of registering DLLs- What does registering a DLL do?
变化是永恒的主题
我们做了一个智能零售结算平台
Analysis of dart JSON encoder and decoder
my. INI file not found
Why should the gradient be manually cleared before back propagation in pytorch?
ActiveMQ的基础
What does a really excellent CTO look like in my eyes
Max of PHP FPM_ Some misunderstandings of children
达梦数据库的物理备份和还原简解
Boost.Asio Library
How to design a high concurrency system
Torch learning notes (5) -- autograd