Explain in detail the arithmetic operators related to matrix operation in MATLAB (addition, subtraction, multiplication, division, point multiplication, point division, power)

Operation is the basis of algorithm , Therefore, it is necessary for us to understand how the tools we use realize the basic operations of matrices .

This blog post concludes MATLAB Arithmetic operators of matrices in .

01- Operator “+”

A+B Representation matrix A and B Add the corresponding elements of ,A and B Must be a matrix of the same size , Unless one of them is scalar .
The first example of this situation is as follows (A、B Are matrices of the same size )：

A = [1 2 3;4 5 6;7 8 9];
B = [2 3 4;5 6 7;8 9 0];
C = A+B;

Running results ：



A second example of this situation is as follows (A、B One of them is a matrix , One is scalar )：

A = [1 2 3;4 5 6;7 8 9];
b = 5;
C = A+b;

02- Operator “-”

A-B Representation matrix A And matrix B The corresponding elements in the are subtracted .A and B Must be a matrix of the same size , Unless one of them is scalar . Operator “-” You can also find the opposite number of each element in the matrix .
Operator “-” The first example code for (A、B All are matrices )

A = [1 2 3;4 5 6;7 8 9];
B = [2 3 4;5 6 7;8 9 0];
C = B-A;

Operator “-” The second example code of (A、B One of them is a matrix , One is scalar )

A = [1 2 3;4 5 6;7 8 9];
b = 2;
C = b-A;
D = A-b;

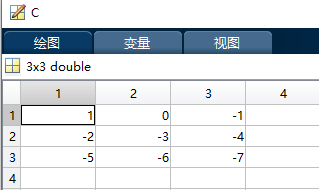
Operator “-” The third example code of ( Find the opposite number of each element in the matrix )

A = [1 2 3;4 5 6;7 8 9];
B = -A;

The operation results are as follows ：

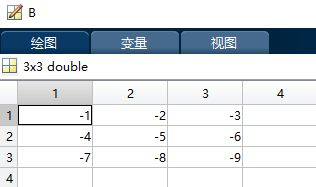
03- Operator “.*”

function ：A.*B It's equivalent to a matrix A And matrices B Multiply the corresponding elements ,A and B Must be a matrix of the same size , Unless one of them is scalar .
Operator “.*” The first example code for ：

A = [1 2 3;4 5 6;7 8 9];
B = [2 3 4;5 6 7;8 9 0];
C = A.*B;

Running results ：

Operator “.*” The second example code of ：

A = [1 2 3;4 5 6;7 8 9];
b = 3;
C = A.*b;
D = b.*A;

The operation results are as follows ：

04- Operator “./”

function ： Operator “./” Is the right division of elements ,A./B It means A Elements in a matrix divided by B The corresponding element in the matrix ,A and B Must be a matrix of the same size , Unless one of them is scalar .
Operator “./” The first example code for is as follows ：

B = [1 2 3;4 5 6;7 8 9];
A = [2 6 12;20 30 42;56 72 90];
C = A./B;

The operation results are as follows ：



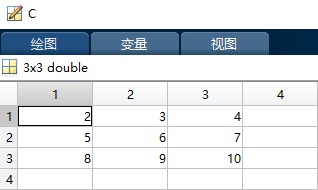
Operator “./” The second example code for is as follows ：

A = [3 6 9;12 15 18;21 24 27];
b = 3;
C = A./b;

The operation results are as follows ：

05- Operator “.\”

Operator “.\” Is the left division of elements , This operator and the operator “./” Use the same method , Just change the position of the divisor and the dividend , namely A.\B It means B Elements in a matrix divided by A The corresponding element in the matrix ,A and B Must be a matrix of the same size , Unless one of them is scalar .
The example is brief ！

06- Operator “.^”

effect ： Operator “.^” Is the power of the elements in the matrix .A.^B It means A Elements in are base numbers ,B The corresponding elements in are exponents . Again A and B Must be a matrix of the same size , Unless one of them is scalar .
Operator “.^” The sample code of is as follows ：

A = [1 2 3;4 5 6;7 8 9];
B = [9 8 7;6 5 4;3 2 1];
C = A.^B;

The operation results are as follows ：

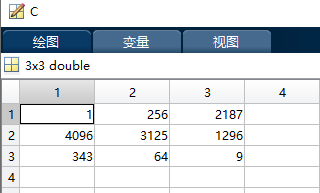
07- Operator “.'” And operators “ ’ ”

Operator “.'” And operators “ ’ ” Are used to find the transpose of a matrix , The difference lies in the treatment of complex matrices , The former is used to find the transpose of complex matrix , Do not find the conjugate complex number of each element , The latter is used to find the transpose of the complex matrix , Will find the conjugate complex number of each element .
The sample code is as follows ：

A = [1 2 3;4 5 6];
B = A.';
C = A';

D = [1+2i 3+4i 5+6i];
E = D.';
F = D';

The operation results are as follows ：

08- Operator “*”

effect ：A*B According to matrix A And matrices B Multiplication of , When A and B When both are matrices , According to the operation rules of matrix multiplication ,A The number of columns of must be equal to B The number of rows is equal . If you don't want to meet this condition and use this operator , Unless one of them is scalar , At this time there is A*b=A.*b
The sample code is as follows ：

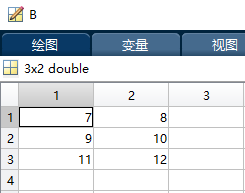
A = [1 2 3;4 5 6];
B = [7 8;9 10;11 12];
C = A*B;

b = 3;
D = A*b;
F = A.*b;

The operation results are as follows ：

09- Operator “/” And operators “\”( Be careful : This is very different from the left-right division of elements )

Operator “/” And operators “\” Matrix right division matrix left division . We know that a matrix has no definition of division , The related concept in linear algebra is the inverse of matrix .
that A\B and B/A What do they stand for ？
Regardless of the accuracy of the results ：A\B amount to inv(A)*B
Regardless of the accuracy of the results ：B/A amount to B*inv(A)
Special attention should be paid here ：A\B It's not like the element division B/A, The law is the inverse of the matrix pressed by the slash .
The example and validation code are as follows ：

A = [1 2;3 4];
B = [5 6;7 8];

C = A\B;
E = inv(A)*B;

D = B/A;
F = B*inv(A);

The operation results are as follows ：


so C and E The result is the same , explain A\B amount to inv(A)*B


so D and F The result is the same , explain B/A amount to B*inv(A)

10- Operator “^”

Operator “^” Is a matrix power operation , Notice in the formula A^B in ,A and B It cannot be a matrix at the same time , The usage is as follows ：
When A and B When both are scalars , For scalar A Of B Power .
When A For the square ,B When it is a positive integer , According to matrix A Of B Times product ;
When A For the square ,B When is a negative integer , According to matrix A The inverse of B Times product ;
When B Is a non integer , It has the following expression ：

Operator “^” The sample code of is not posted .