【GCN-RS】Are Graph Augmentations Necessary? Simple Graph Contrastive Learning for RS (SIGIR‘22)

Are Graph Augmentations Necessary? Simple Graph Contrastive Learning for Recommendation (SIGIR’22)

This article attacks that graph contrast learning does not necessarily extend graph structure ,SGL That method is complex and the benefit is weak ：

The article is in SGL On the basis of , The test does not amplify the graph structure , Direct comparative learning ：
$${\mathcal{L}}_{cl}=\sum _{i\in \mathcal{B}}-\log \frac{\exp \left({\mathbf{z}}_i^{\prime \top }{\mathbf{z}}_i^{\prime \prime }/\tau \right)}{{\sum }_{j\in \mathcal{B}}\exp \left({\mathbf{z}}_i^{\prime \top }{\mathbf{z}}_j^{\prime \prime }/\tau \right)}$$
I have also done experiments , Set the molecule of this formula to 1, That is, the characterization is still similar without considering the structure of the amplification diagram ,NDCG Instead, the index rose higher , therefore SGL It's really not very useful .

This paper presents a very simple method , Directly in embedding Make a disturbance on , Fixed graph structure ：

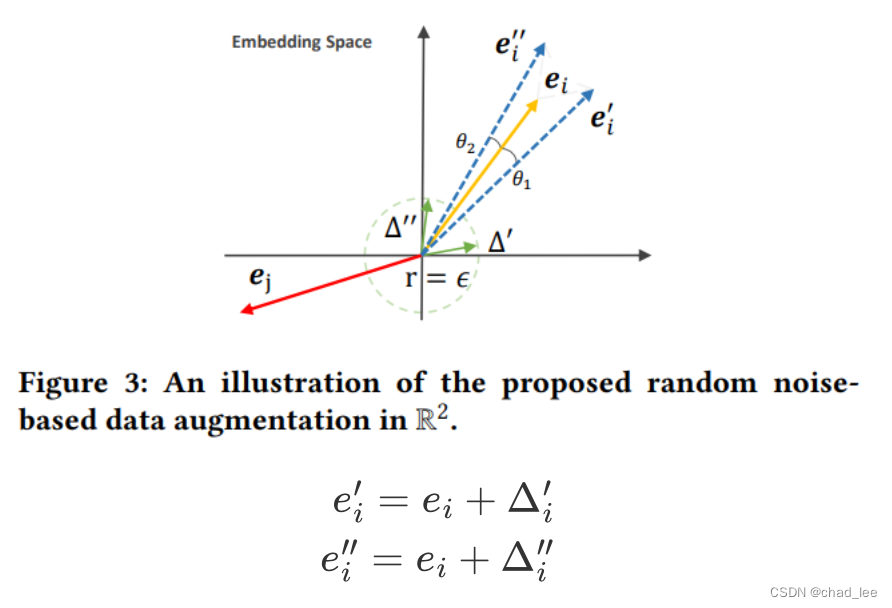
$$\begin{array}{r}{e}_i^{\prime }=e_i+{\Delta }_i^{\prime }\\ e_i^{\prime \prime }=e_i+{\Delta }_i^{\prime \prime }\end{array}$$
among ${\Delta }_i^{\prime },{\Delta }_i^{\prime \prime }$ They are random disturbances ,$\Delta =\bar{\Delta }\odot \mathrm{sign}\left(e_i\right),\mathrm{sign}(\mathrm{x}),x<0$ The output -1, otherwise 1.$\bar{\Delta }\sim U(0,1)$. Therefore, these two disturbances can be regarded as in the primitive embedding The direction of , They have expanded a little . Then bring in comparative learning loss, You can use it .

In terms of implementation, it is simpler to be violent , Just on each floor embedding Just add disturbance ：
$$\begin{array}{r}{\mathbf{E}}^{\prime }=\frac{1}{L}\left(\left({\tilde{\mathbf{A}}}^{(0)}+{\Delta }^{(1)}\right)+\left(\tilde{\mathbf{A}}\left(\tilde{\mathrm{A}}{\mathrm{E}}^{(0)}+{\Delta }^{(1)}\right)+{\Delta }^{(2)}\right)\right)+\dots \\ +\left({\tilde{\mathbf{A}}}^L{\mathbf{E}}^{(0)}+{\tilde{\mathbf{A}}}^{L-1}{\Delta }^{(1)}+\dots +\tilde{\mathbf{A}}{\Delta }^{(L-1)}+{\Delta }^{(L)}\right))\end{array}$$