当前位置:网站首页>Dsolve function of sympy
Dsolve function of sympy
2022-06-29 10:08:00 【It's mally!】
Notes
translate official sympy Kuzhi ODE
Want to use sympy Solving linear equations , But there is too little information on the Internet , Just want to try to translate .
Later it was found that there was 2 A good blog , Portal 1, Portal 2
User Functions
dsolve The function belongs to this user functions Within the scope of .
These functions use from sympy import * Import global namespace . These functions ( Unlike hint Functions), It is only for ordinary users Sympy.
s y m p y . s o l v e r s . o d e . d s o l v e \color{#008b45}{sympy.solvers.ode.dsolve} sympy.solvers.ode.dsolve
( ∗ e q ∗ , ∗ f u n c = N o n e ∗ , h i n t = ′ d e f a u l t ′ , s i m p l i f y = T r u e , i c s = N o n e , x i = N o n e , ∗ e t a = N o n e ∗ , ∗ x 0 = 0 ∗ , ∗ n = 6 ∗ , k w a r g s ) \color{#008b45}(*eq*, *func=None*, hint='default', simplify=True, ics=None, xi=None, \\*eta=None*, *x0=0*, *n=6*, kwargs) (∗eq∗,∗func=None∗,hint=′default′,simplify=True,ics=None,xi=None,∗eta=None∗,∗x0=0∗,∗n=6∗,kwargs)
Can solve any ( Supported by ) Ordinary differential equations and systems of ordinary differential equations .
For simple ordinary differential equations
Usage
The number of equations in the system of equations is 1,
d s o l v e ( e q , f ( x ) , h i n t ) \color{#008b45}dsolve(eq, f(x), hint) dsolve(eq,f(x),hint) -> Usage method hint In ordinary differential equations eq To solve the problem f(x).
Details
- eq It can be any ordinary differential equation that can be supported . It can be an equation , It can also be an expression , Suppose it equals 0.
- f(x) Its derivatives make up the differential equation . in the majority of cases , We don't need to provide it , It will be calculated automatically ( If it cannot be calculated, an error will be reported )
- hint It's what you want dsolve Solution method used . Use c l a s s i f y _ o d e ( e q , f ( x ) ) \color{#008b45}{classify\_ode(eq, f(x))} classify_ode(eq,f(x)) You can get one ODE All the methods that can be used . By default c l a s s i f y _ o d e ( ) \color{#008b45}{classify\_ode()} classify_ode().
- simplify It can be used o d e s i m p ( ) \color{#008b45}{odesimp ()} odesimp() To simplify the . For more information , See its DocString. for example , Turn this option off to disable func Solution or simplification of any constant . It will still integrate with this hint . Be careful , If this option is enabled , The solution may involve more than ODE The order of more arbitrary constants .
- xi and eta Is an infinitesimal function of an ordinary differential equation . They are infinitesimals of Lie groups of invariant point transformations of differential equations . The user can specify a value for infinitesimal . If not specified ,xi and eta Will be used with the help of various Heuristics i n f i n i t e s i m a l s ( ) \color{#008b45}{infinitesimals()} infinitesimals() Calculate .
- ics Is the initial of the differential equation / Set of boundary conditions . It should be in a form similar to { f ( x 0 ) : x 1 , f ( x ) . d i f f ( x ) . s u b s ( x , x 2 ) : x 3 } \color{#0000ff}{\{f(x0): x1, f(x).diff(x).subs(x, x2): x3\}} { f(x0):x1,f(x).diff(x).subs(x,x2):x3} give . For power series solutions , If no initial condition is specified , Then assume f(0) by c0, The solution of the power series is 0.
- x0 It's the point that needs to be solved .
- n Give the index of the variable to be solved
Hints
Jump first
Tips
- You can declare the derivative of an unknown function like this :
from sympy import Function,Derivative
from sympy.abc import x # x Is an independent variable
f= Function("f")(x) #f yes x Function of
f_=Derivative(f,x) #f_ yes f Yes x The derivative of
- stay test_ord .py You can see a series of how to use d s o l v e ( ) \color{#008b45}{dsolve()} dsolve() An example of .
- d s o l v e ( ) \color{#008b45}{dsolve()} dsolve() Always return an equality class ( Except the hint is all or all_Integral The situation of ). If possible , It will explicitly solve for the function being solved . otherwise , It returns an implicit solution . Any constant is called C1、C2 Symbols for, etc .
- Because all solutions are mathematically equivalent , So for ODE, Some prompts may return identical results . however , Usually two different prompts return the same solution in different formats . The two should be equivalent . Also pay attention to , Sometimes the values of any constant in two different solutions may be different , Because a constant can be “ absorption ” Other constants .
- use h e l p ( o d e . o d e < h i n t n a m e > ) \color{#008b45}{help(ode.ode_<hintname>)} help(ode.ode<hintname>) You can get more information about specific tips , One of them is without _Integral The name of the prompt for .
For ordinary differential equations
Usage
d s o l v e ( e q , f u n c ) \color{#008b45}{dsolve(eq, func)} dsolve(eq,func) -> Xie Changyou x(t),y(t),z(t) And so on eq.
Details
eq It can be an arbitrarily supported system of ordinary differential equations. It can be an equation , It can also be an expression , Suppose it equals 0.
func set up x(t) and y(t) Is a function of a variable , The variable and its partial derivatives constitute a system of ordinary differential equations . It will be automatically detected ( If you cannot detect , Will cause an error ).
Examples
from sympy import Function, dsolve, Eq, Derivative, sin, cos, symbols
from sympy.abc import x
f=Function('f')
ans=dsolve(Derivative(f(x),x,x)+9*f(x),f(x))
print(ans)
#Eq(f(x), C1*sin(3*x) + C2*cos(3*x))
边栏推荐
猜你喜欢
Nacos环境隔离

Perfect binary tree, complete binary tree, perfect binary tree

linux环境下安装配置redis,并设置开机自启动

2020-09-29 非商品模板化代码层次 rapidjson库
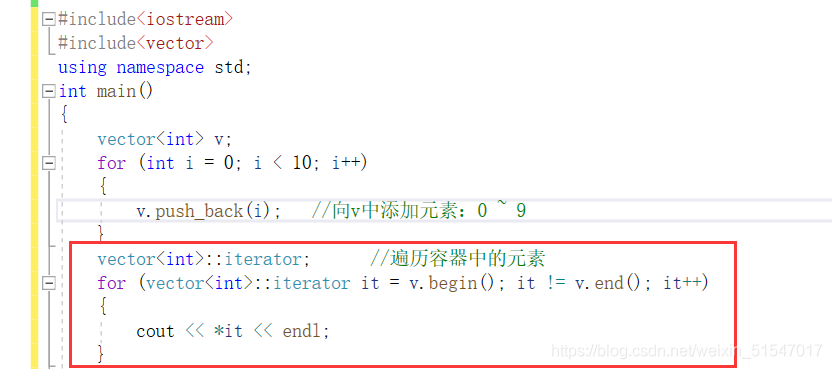
How to traverse objects in the vector container

Flutter 基础组件之 GridView

阿里云防火墙配置,多种设置方式(iptables和fireward)

Container of the basic component of the flutter

Alternative implementation of Scrollview pull-down header amplification

Generic paging framework
随机推荐
Gross Tumor Volume Segmentation for Head and Neck Cancer Radiotherapy using Deep Dense Multi-modalit
自定义控件之下载控件1(DownloadView1)
FreeRTOS (VIII) - time management
Student addition / deletion gaih
2019.10.30学习总结
使用Rancher搭建Kubernetes集群
Summary of PHP memory horse technology research and killing methods
2020-09-25 boost库的noncopyable,用于单例模式
另类实现 ScrollView 下拉头部放大
点在多边形内外的判断
GridView of basic component of shutter
ORA-01950 对表空间无权限
Gmail: how to quickly read all messages
2020-09-23左右值 右值引用 std::move()
JVM之TLAB
在Activity外使用startActivity()方法报错原因与解决办法
2020-09-18 referer认证 url转义
C语言中通过sprintf()函数构造sql语句
RecyclerView 粘性(悬浮)头部
Setinterval, setTimeout and requestanimationframe