当前位置:网站首页>【LeetCode】98.验证二叉搜索树
【LeetCode】98.验证二叉搜索树
2022-08-04 10:50:00 【酥酥~】
题目
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1: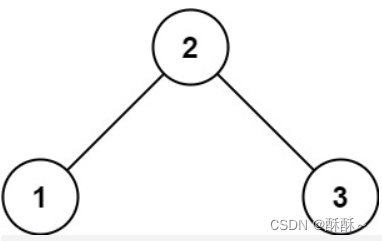
输入:root = [2,1,3]
输出:true
示例 2: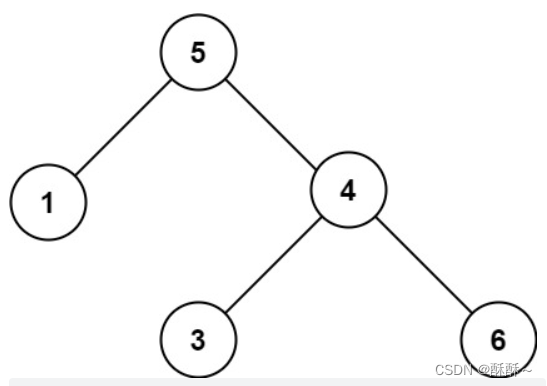
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1
题解
递归方法,记录上下界
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */
class Solution {
public:
bool fun(TreeNode* root,long long left,long long right)
{
if(root == nullptr)
return true;
if(root->val <= left || root->val >= right)
return false;
return fun(root->left,left,root->val) && fun(root->right,root->val,right);
}
bool isValidBST(TreeNode* root) {
return fun(root,LONG_MIN,LONG_MAX);
}
};
利用中序遍历方法
得到的数列是有序的升序序列
那么该结点值必然小于前一个被遍历的结点
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> mystack;
long long pre = LONG_MIN;
while(!mystack.empty() || root!=nullptr)
{
while(root)
{
mystack.emplace(root);
root = root->left;
}
root = mystack.top();
mystack.pop();
if(root->val <= pre)
return false;
pre = root->val;
root = root->right;
}
return true;
}
};
边栏推荐
猜你喜欢
随机推荐
Heap Sort
标准C语言学习总结12
Business collocations
Introduction to Mysql storage engine
图文手把手教程--ESP32 一键配网(Smartconfig、Airkiss)
LeetCode第三题(Longest Substring Without Repeating Characters)三部曲之三
华为开源:聚焦开源基础软件,共建健康繁荣生态
Oracle中对临时表空间执行shrink操作
C language * Xiaobai's adventure
mysql进阶(二十六)MySQL 索引类型
HCIP 第十八天
cubemx stm32 afm3000模块 气体流量传感器 驱动代码
从零开始Blazor Server(7)--使用Furion权限验证
《迁移学习导论》第2版,升级内容抢先看!
Advanced transcriptome analysis and R data visualization hot registration (2022.10)
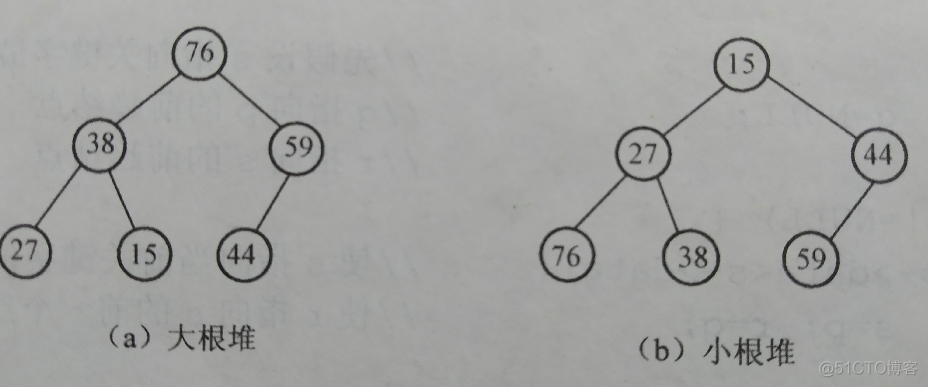
二叉树与堆
mae,mse,rmse分别利用sklearn和numpy实现
There are 12 balls, including 11 weight, only one, don't know is light or heavy. Three times in balance scales, find out the ball.
iMeta | Baidu certification is completed, search "iMeta" directly to the publisher's homepage and submission link
AWS Lambda相关概念与实现思路